• [ ] 347.前k个高频元素 :::info 前提：

    • 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。

    • 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
    • 你可以按任意顺序返回答案

    优先级队列。就是一个披着队列外衣的堆
    什么是堆呢？
    堆是一颗完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。
    如果父亲结点是大于等于左右孩子就是大顶堆（堆头是最大元素），小于等于左右孩子就是小顶堆（堆头是最小元素）。
    直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。 :::

    代码：（详细注释）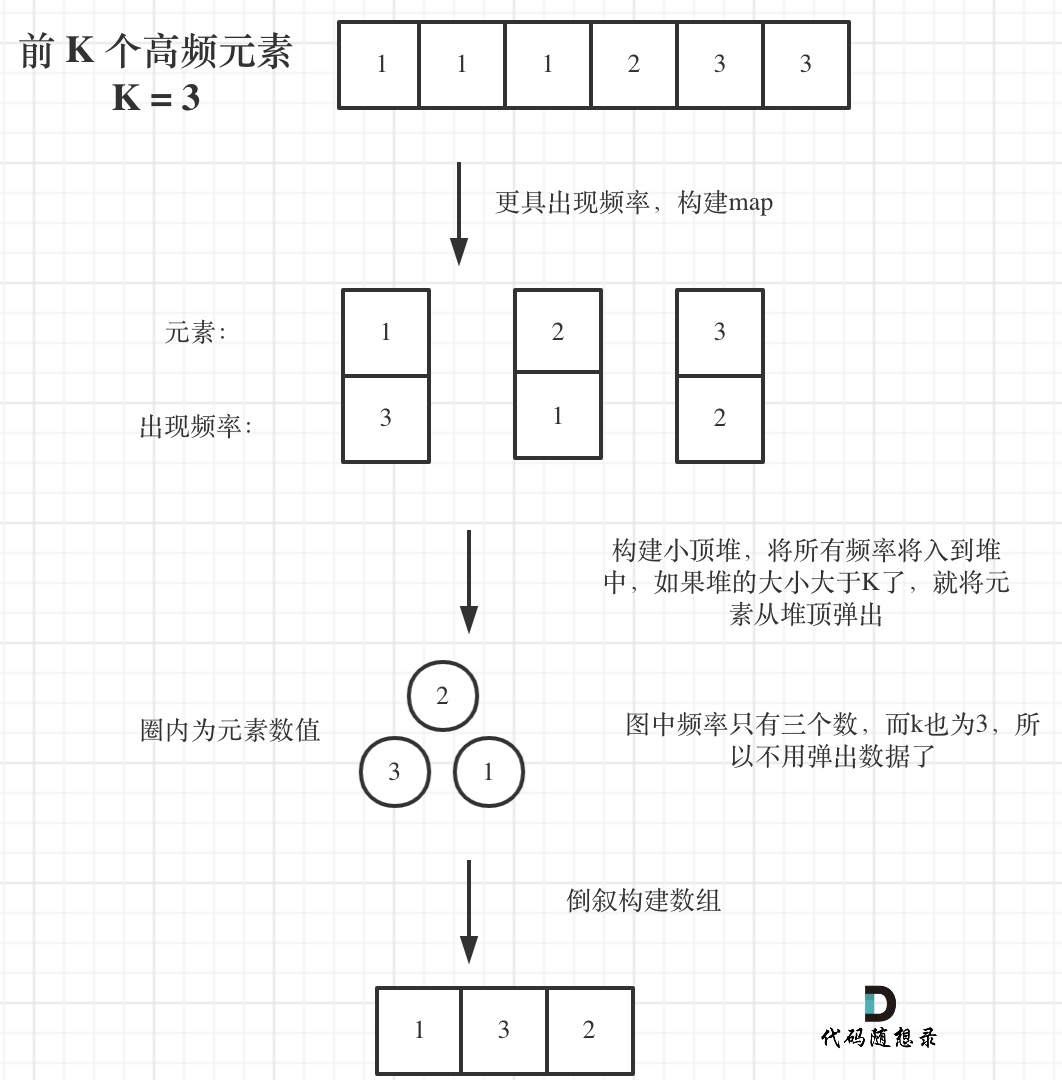
    前k个高频元素 - 图1

    1. // 时间复杂度：O(nlogk)
    2. // 空间复杂度：O(n)
    3. class Solution {
    4. public:
    5.     // 小顶堆
    6.     class mycomparison {
    7.     public:
    8.         bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
    9.             return lhs.second > rhs.second;
    10.         }
    11.     };
    12.     vector<int> topKFrequent(vector<int>& nums, int k) {
    13.         // 要统计元素出现频率
    14.         unordered_map<int, int> map; // map<nums[i],对应出现的次数>
    15.         for (int i = 0; i < nums.size(); i++) {
    16.             map[nums[i]]++;
    17.         }
    19.         // 对频率排序
    20.         // 定义一个小顶堆，大小为k
    21.         priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;
    23.         // 用固定大小为k的小顶堆，扫面所有频率的数值
    24.         for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {
    25.             pri_que.push(*it);
    26.             if (pri_que.size() > k) { // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
    27.                 pri_que.pop();
    28.             }
    29.         }
    31.         // 找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒叙来输出到数组
    32.         vector<int> result(k);
    33.         for (int i = k - 1; i >= 0; i--) {
    34.             result[i] = pri_que.top().first;
    35.             pri_que.pop();
    36.         }
    37.         return result;
    39.     }
    40. };

    分析：
    左大于右就会建立小顶堆，反而建立大顶堆
    为什们不用快排