:::info
哈希表是根据关键码的值而直接进行访问的数据结构。
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法了。
:::
比如说数组就是以这样哈希表
它的关键码就是引索下标。
:::danger
而且如果哈希值比较少、特别分散、跨度非常大,使用数组就造成空间的极大浪费。
:::
可以知道,有了哈希表,查找数据就是O(1)的时间
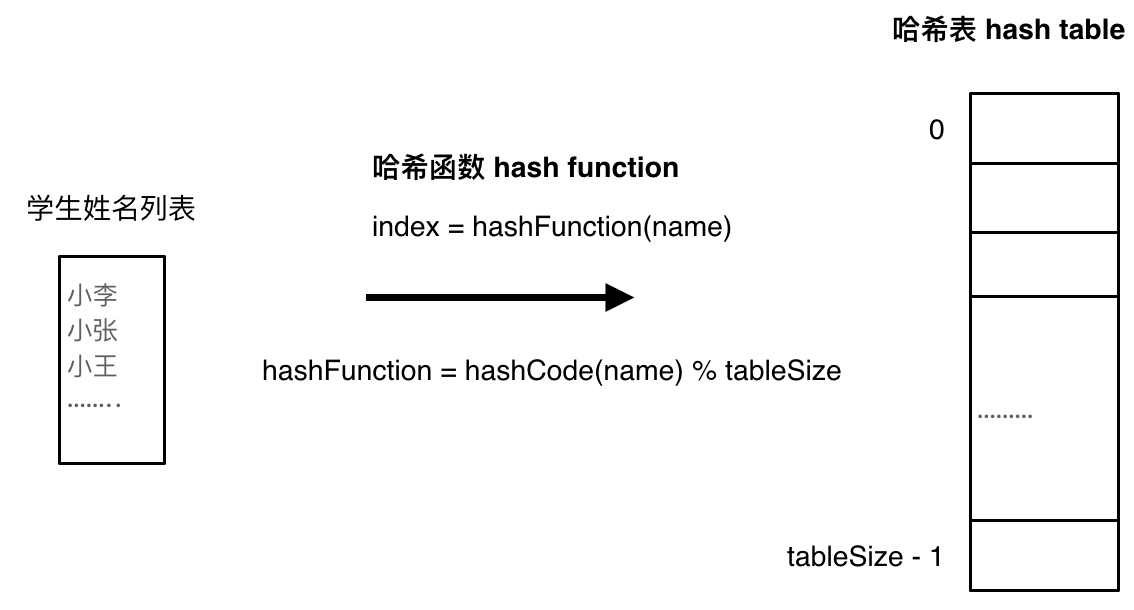
但是要把要查找的内容映射到可以直接访问的index,或者key,需要一个哈希函数。
常见的三种哈希结构
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
- array 数组
- set 集合
- map 映射
来对比一下集合与映射:
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::set | 红黑树 | 有序 | 否 | 否 | O(logn) | O(logn) |
| std::multiset | 红黑树 | 有序 | 是 | 否 | O(logn) | O(logn) |
| std::unordered_set | 哈希表 | 无序 | 否 | 否 | O(1) | O(1) |
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(logn) | O(logn) |
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(logn) | O(logn) |
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
怎么选择呢
- 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
- set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下表位置,因为要返回x 和 y的下表。所以set 也不能用。
此时就要选择另一种数据结构:map ,map是一种key value的存储结构,可以用key保存数值,用value在保存数值所在的下表。

