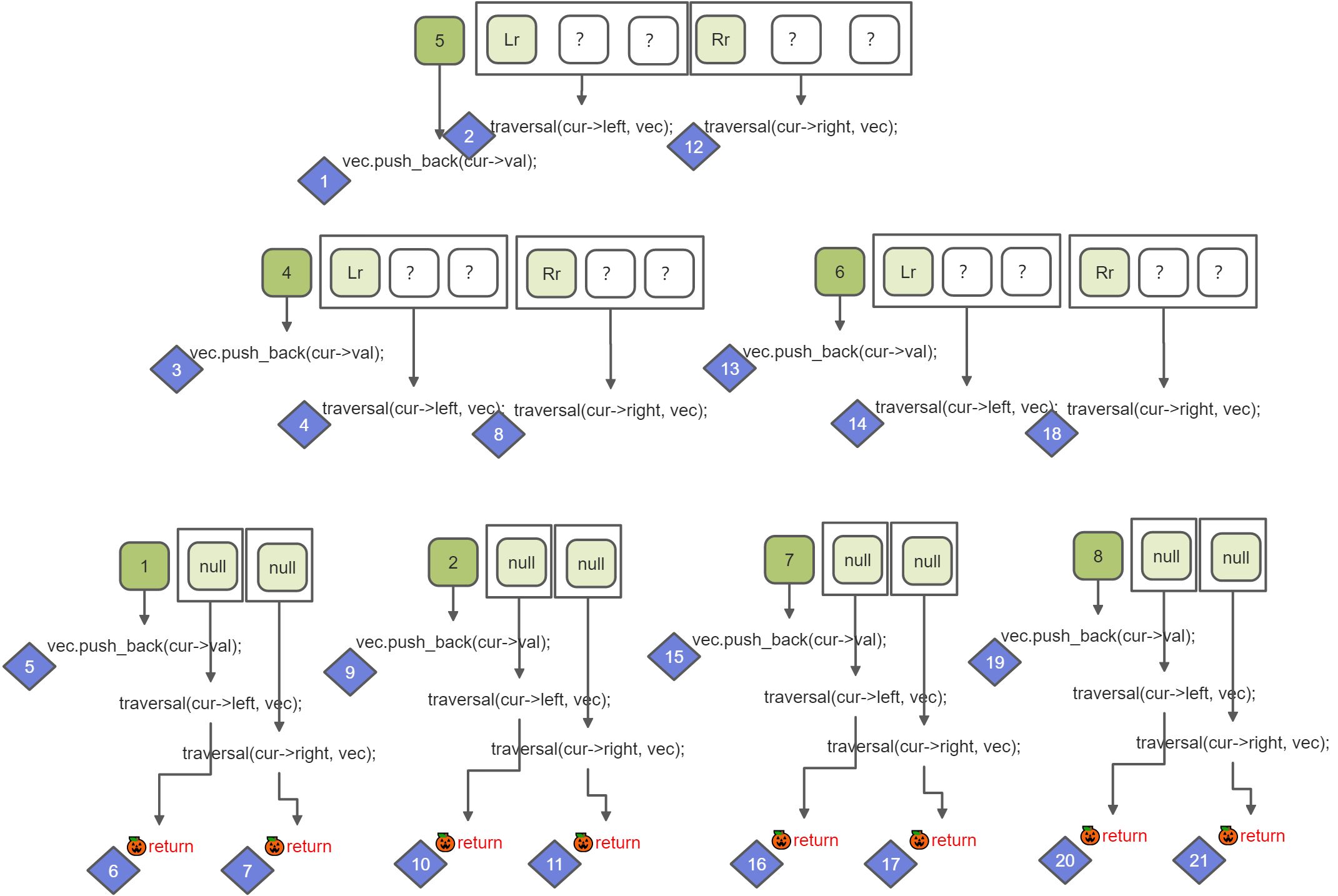
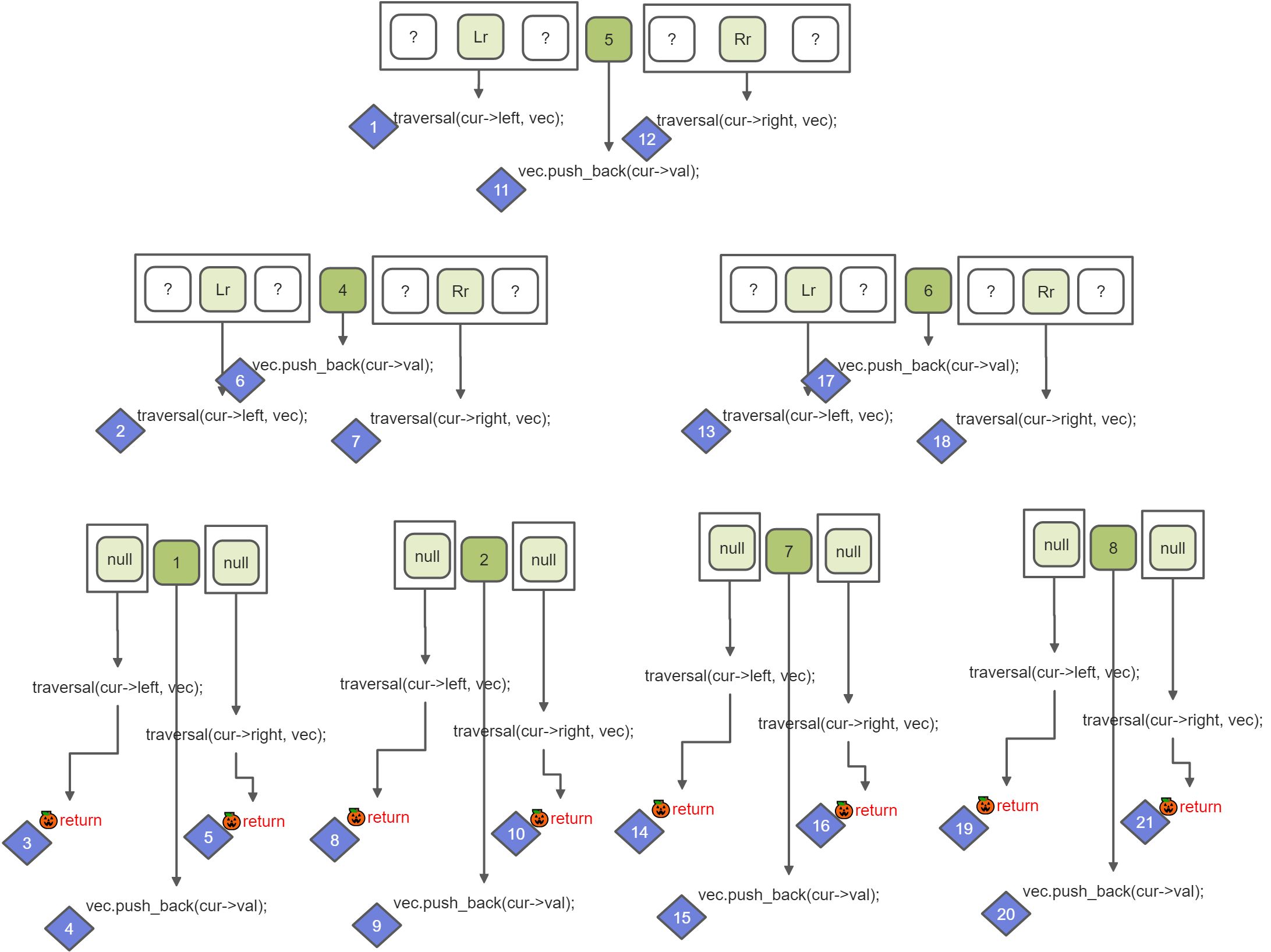
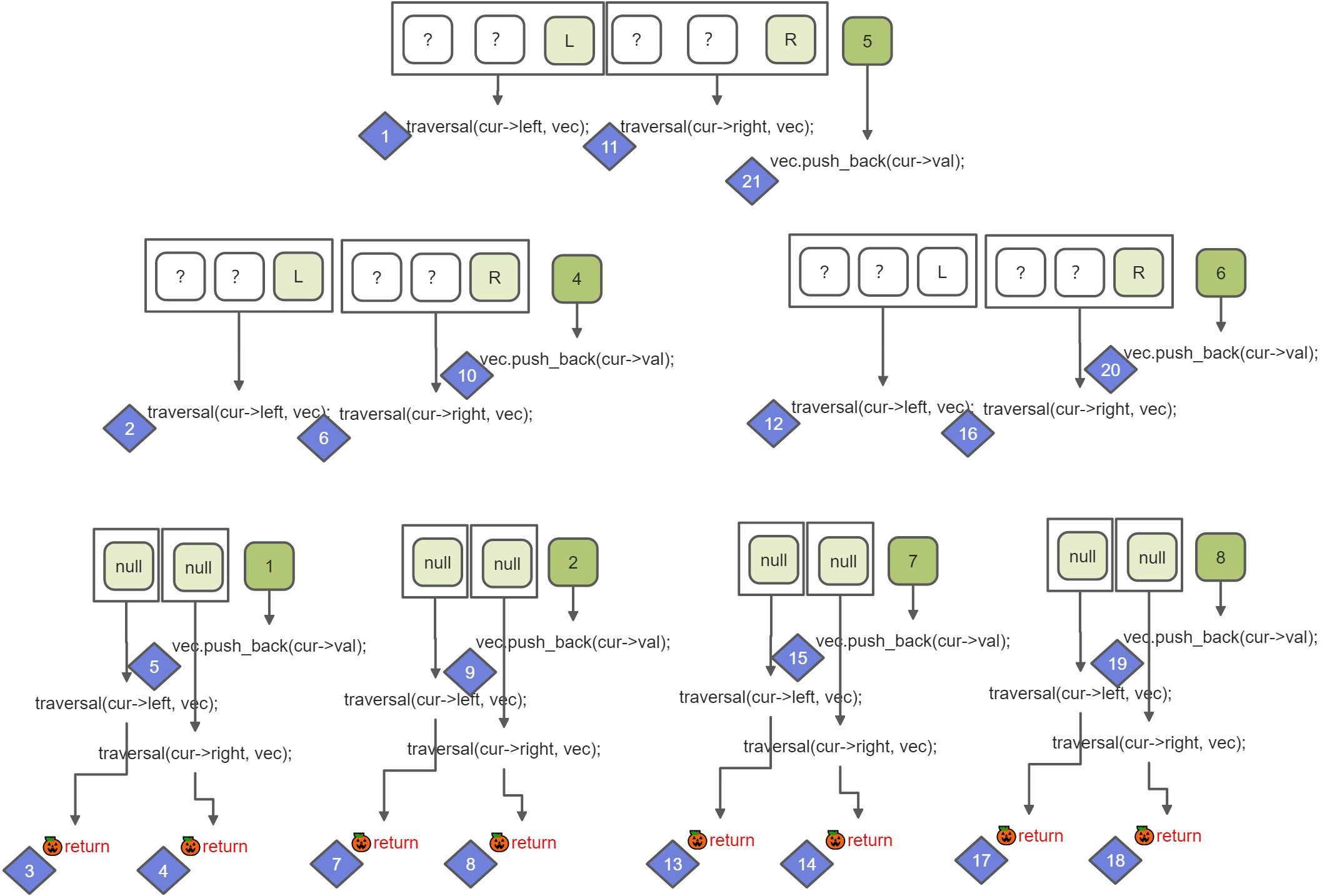
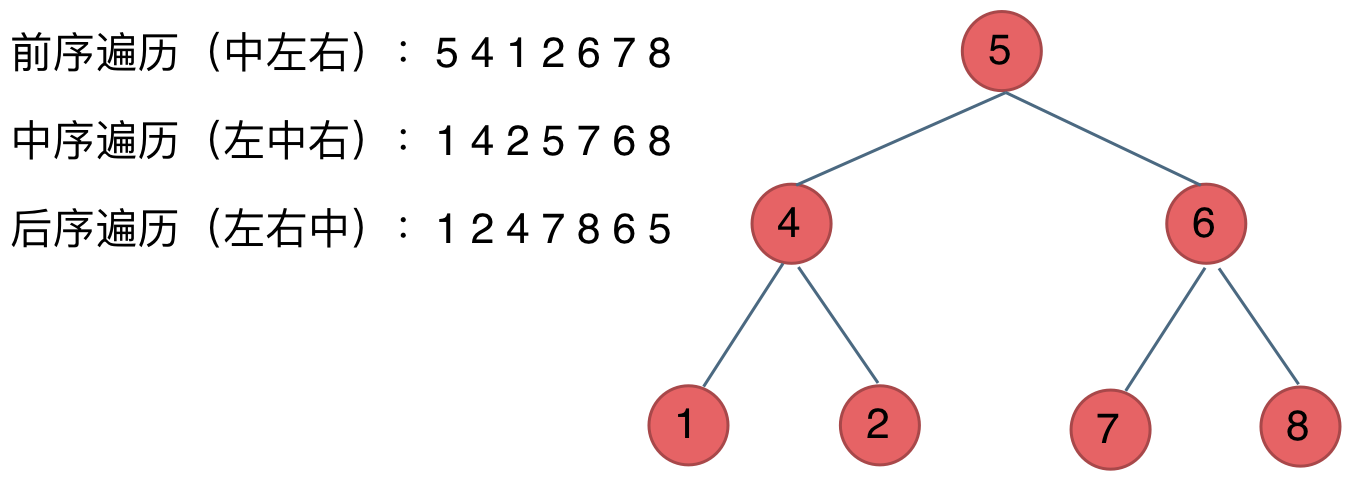
不同叫法指的是父结点在前中后出现，其它结点从左到右出现。

• 前序
• 中序
• 后序

:::info 递归和迭代的异同：

• 递归是在查找同时处理（压入输出数组）了，
• 迭代是经过一个缓存器，把查找的结果边保存边处理 :::

  统一递归法

  递归三部曲

  找到算法的最终结构，或者数学上的表达式，就好设计递归架构。

  1、确定参数、返回值

  2、确定终止条件

  3、确定单层递归的逻辑

  递归代码

  可以认为每一层迭代都可以确定三个元素，其他子元素在下一层进行插缝。 从下面的分析图可以看出，递归需要有自相似性

前序遍历

class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

中序遍历

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    vec.push_back(cur->val);    // 中
    traversal(cur->right, vec); // 右
}

后序遍历

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    traversal(cur->right, vec); // 右
    vec.push_back(cur->val);    // 中
}

统一迭代法

注意栈是先进后出，所以压入顺序得反着来

以中序为例：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> st; // 缓冲器，用来保存从输入获取的节点
        vector<int> result; //结果储存数组
        if(root!=nullptr)//如果不为空则压入缓冲器，空则什么都不做，之后只要判断缓冲器是否为空
            st.push(root);
        while(!st.empty()){ //开始循环更新缓冲器和结果数组
            TreeNode *node = st.top(); //首先取出栈顶元素，保存到临时变量
            st.pop();//取完要记得弹出
            if(node!=nullptr){ //非空则进行访问，更新缓冲器。
                if(node->right) 
                    st.push(node->right); //right node因为是stack，所以要先右再左
                st.push(node); // middle node 
                 // 🎃中节点已经被访问过，但是还没处理，所以用空节点标记，不再访问直接处理
                st.push(nullptr);  
                if (node->left)  //left node
                    st.push(node->left);
            }else{ //空则进行处理，更新结果数组，取空结点后一位,移入结果中
                st.pop(); //弹出空结点
                node = st.top();  //取出栈中元素
                st.pop();
                result.push_back(node->val); //压入结果数组中
            }
        }
        return result;
    }
};

要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
动画中，result数组就是最终结果集。
可以看出我们将访问的节点直接加入到栈中，但如果是处理的节点则后面放入一个空节点， 这样只有空节点弹出的时候，才将下一个节点放进结果集。

因为是栈，所以下面顺序都是反的

前序

if (node != NULL) {
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
                st.push(node);  st.push(NULL);
            }

后序

if (node != NULL) {
                st.push(node); st.push(NULL);
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
            }

vetor<int> inorderTraversal(TreeNode* root){
    vector<int> result;
    stack<TreeNode*> st;
    if(root!=nullptr) st.push(root);
    while(!st.empty()){
        TreeNode* node = st.top();
        st.pop();
        if(node!=nullptr){
            if(node->right) st.push(node->right);
            st.push(node); st.push(nullptr);
            if(node->left) st.push(node->left);
        }else{
            st.pop(); //pop NULL
            node = st.top();
            st.pop();
            result.push_back(node->val);
        }
    }
    return result;
}