Trie 字典树

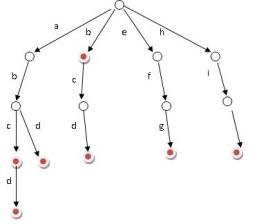
Trie，又称单词查找树、字典树，是一种树形结构，是哈希树的变种。其有三个基本性质：

• 根节点不包含字符，除根节点外的每一个节点都只包含一个字符
• 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串
• 每个节点的所有子节点包含的字符都不相同

基本操作：查找、插入和删除，其中删除操作比较少

缺点：占用大量空间，一个节点只存储一个字符

压缩字典树：Compressed Trie，操作更加复杂，耗时更多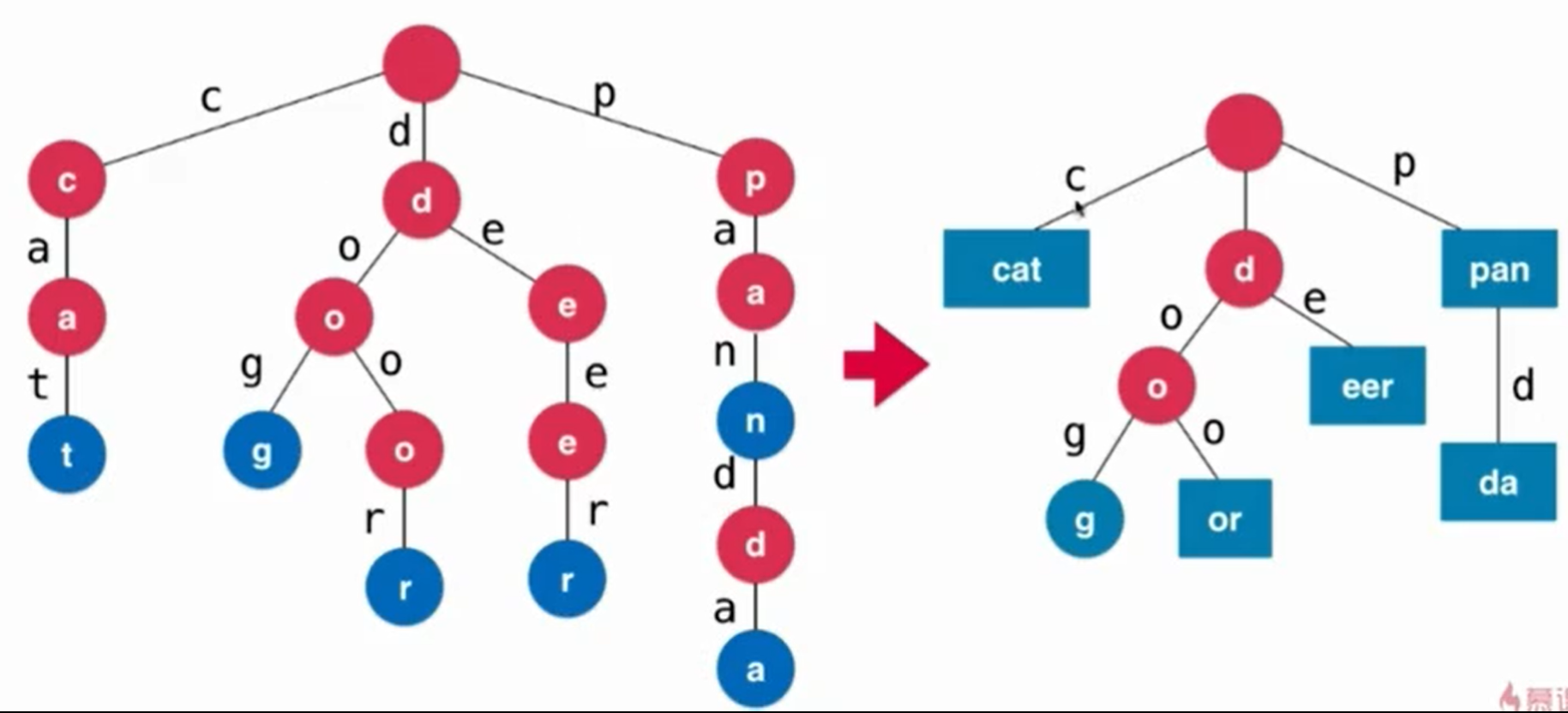

与之相关的其他数据结构：

• Ternary Search Trees：三分搜索树
• Suffix Tree：后缀树

与字符串相关 — 子串查询：

• KMP
• Boyer-Moore
• Rabin-Karp

文件压缩、模式匹配、编译原理

应用

1、最长公共子串：对所有串建立字典树，对于两个串的最长公共前缀的长度即他们所在的结点的公共祖先个数，于是，问题就转化为当时公共祖先问题

2、串排序：

• 问题：给定N个互不相同的仅由一个单词构成的英文名，让你将他们按字典序从小到大输出
• 解法：用字典树进行排序，采用数组的方式创建字典树，这棵树的每个结点的所有儿子很显然地按照其字母大小排序。对这棵树进行先序遍历即可

3、串的快速检索：

• 问题：给出N个单词组成的熟词表，以及一篇全用小写英文书写的文章，请你按最早出现的顺序写出所有不在熟词表中的生词
• 解法：在这道题中，我们可以用数组枚举，用哈希，用字典树，先把熟词建一棵树，然后读入文章进行比较，这种方法效率是比较高的

4、IP路由（最长前缀匹配）：使用Trie树的最长前缀匹配算法，Internet 协议（IP）路由中利用转发表选择路径

java 实现

public class Trie {
    private class Node {
        // 终止符：指示当前节点是否为某个单词的结尾
        boolean isWord;
        TreeMap<Character, Node> next;
        public Node(boolean isWord) {
            this.isWord = isWord;
            this.next = new TreeMap<>();
        }
        public Node() {
            this(false);
        }
    }
    // 根节点
    private final Node root;
    // 存储的单词数
    private int size;
    public Trie() {
        root = new Node();
        size = 0;
    }
    // 获取Trie中的单词数量
    public int getSize() {
        return size;
    }
    // 添加一个单词
    public void add(String word) {
        Node cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            // 如果不存在此节点，则进行创建
            if (!cur.next.containsKey(c)) {
                cur.next.put(c, new Node());
            }
            // 直接获取，如果节点不存在会在前面创建
            cur = cur.next.get(c);
        }
        if (!cur.isWord) {
            cur.isWord = true;
            size++;
        }
    }
    // 从Trie中查询一个单词
    public boolean contains(String word) {
        Node cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            if (!cur.next.containsKey(c)) {
                return false;
            }
            cur = cur.next.get(c);
        }
        return cur.isWord;
    }
    // 字典树的前缀搜索
    public boolean isPrefix(String prefix) {
        Node cur = root;
        for (int i = 0; i < prefix.length(); i++) {
            char c = prefix.charAt(i);
            if (!cur.next.containsKey(c)) {
                return false;
            }
            cur = cur.next.get(c);
        }
        return true;
    }
}