0.1+0.2 === 0.3 false 对于JS的数字类型的理解

1、javascript 中是如何表示数字的

javascript 使用Number 类型表示数字（整数和浮点型），遵循IEEE754标准 通过64位来表示一个数字，数字在内存中的表示 如下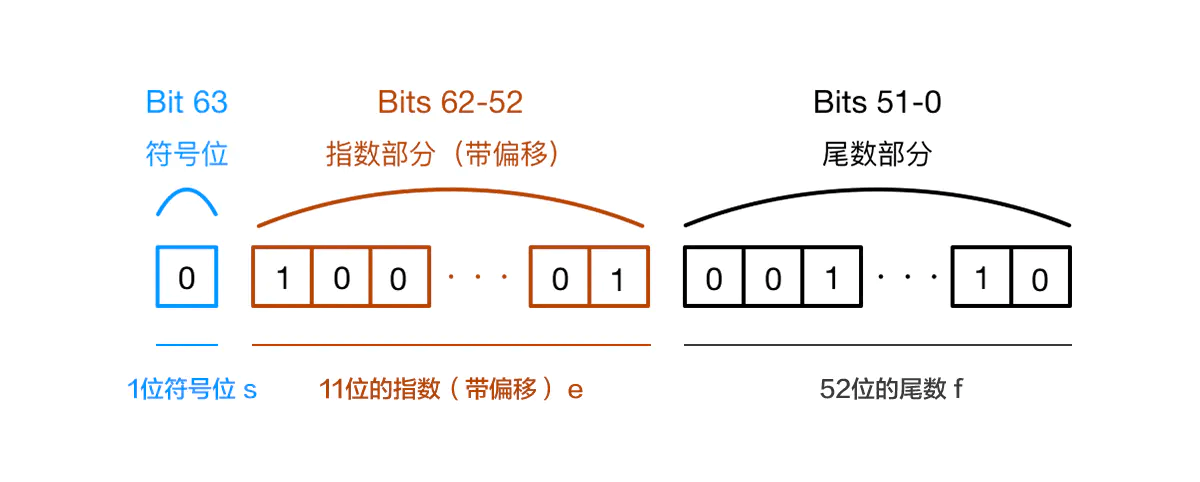

第 0 位： 符号位 0 正 1负
第1-11位 储存指数部分e
第12 - 63位 储存小数部分 即有效数字

补充说明：js 最大安全数 Number.MAX_SAFE_INTEGER == Math.pow(2,53) - 1

因为二进制有效数字总是1.xxxx的形式，尾数部分f 在规约形式下 第一位默认为1 省略不写**
因此，JavaScript提供的有效数字最长为53个二进制位（64位浮点的后52位+被省略的1位）

2、运算时发生了什么

计算机在运算时候 首先会根据IEEE 754 标准转化为2进制 然后进行对阶运算

（1）转化为二进制

0.1 和 0.2 转换成 二进制后会无限循环

0.1 -> 0.0001100110011001...(无限循环)
0.2 -> 0.0011001100110011...(无限循环)

IEEE 754 尾数位数限制，需要将后面多余的位数截掉
可用此网站 做进制转换
https://babbage.cs.qc.cuny.edu/IEEE-754.old/Decimal.html
0.1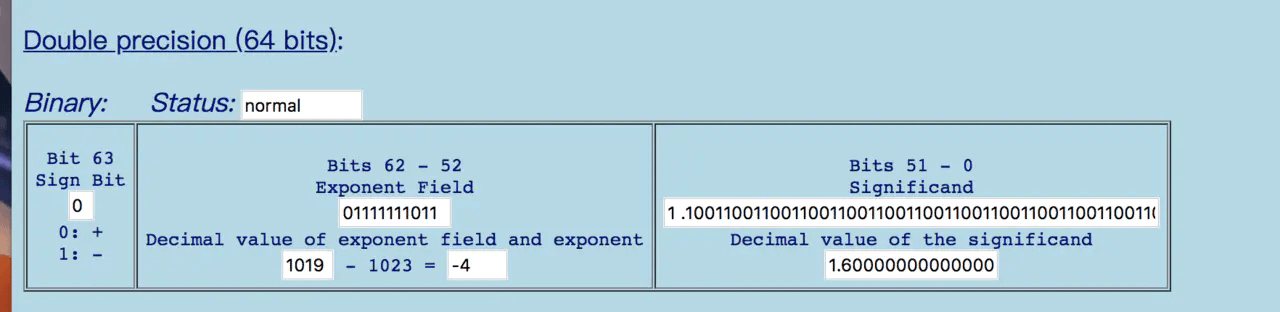

0.2

由此可以看出 在 进制转换的过程中 精度已经丢失了

那为什么 x=0.1 可以得到0.1 呢

标准中规定尾数f的固定长度是52位，再加上省略的一位，这53位是JS精度范围。它最大可以表示2^53(9007199254740992), 长度是 16，所以可以使用 toPrecision(16) 来做精度运算，超过的精度会自动做凑整处理

0.10000000000000000555.toPrecision(16)
// 返回 0.1000000000000000，去掉末尾的零后正好为 0.1
// 但来一个更高的精度：
0.1.toPrecision(21) = 0.100000000000000005551

（2）对阶运算

由于指数位数不相同，运算时需要对阶运算 这部分也可能产生精度损失
按照上面两步运算（包括两步的精度损失），最后的结果是

0.0100110011001100110011001100110011001100110011001100 
十进制为：0.30000000000000004

所以精度的损失 可能出现在 进制转化 和 对阶运算过程中

3、如何解决精度问题

（1）原生方法

思路一：将小数转化为整数进行运算
思路二：限制精度，只保留消暑部分位数 Number.toFixed()

(2) 三方API

math 库：

 //统一配置math.js
    math.config({
        number: 'BigNumber',  
        // 'number' (default), 
        precision: 20         
    });
    // 转换数字类型
    var temp = math.bignumber(a) * math.bignumber(b)
    // 提取数字类型，不然会是一个math对象
    var result = math.number(temp)

bignumber，big，decimal等