启发式算法,比较万能的优化方法。 python库scikit-opt很好用

(b站视频资源,链接丢失了)
| 算法 | 基本原理 | 变量个数 | 整数规划 0-1规划 | TSP | |
|---|---|---|---|---|---|
| Matlab | Python | ||||
| 模拟退火 | 依据最好解 按规则变为新解 | 一个 | √ 自定义规则 | × | √ |
| 遗传算法 | 选择 交叉 变异 | 一个 多种群 | √ 自带 | √ 自带 | √ |
| 粒子群 | 个体 全局 | 多个 | × | × | × |
模拟退火 SA
定义一个解,根据自己设定的产生新解规则,对已知最优解进行改变,迭代寻找最优
讲义
D:\00000MCM\清风\0 课件和代码\公开课:“模拟退火算法”的课件和代码\模拟退火算法直播的讲义PL.pdf
Matlab
使用清风代码(自定义条件实现整数规划)
清风代码:
D:\00000MCM\清风\0 课件和代码\公开课:“模拟退火算法”的课件和代码\模拟退火算法的代码\课堂上用到的
2019D题目 :
D:\00000MCM\0 codes\2019Dsum\q3_sa.m
自带函数 帮助文档
Find minimum of function using simulated annealing algorithm - MATLAB simulannealbnd - MathWorks 中国
matlab模拟退火算法(SA)详解(一)算法入门_viafcccy的博客-CSDN博客_matlab模拟退火算法
(Python)
遗传算法 GA
文章:D:\00000MCM\0 研究生数学建模竞赛历年真题和优秀论文集锦\研究生数学建模-优秀论文\2020年优秀论文\B题\B20105340008.pdf(用于选择关键变量 自定义适应度函数 余弦相似度)
2020B 0019(基本原理 对比试验 种群大小 迭代次数 交叉率 变异率)
0031
0004
Matlab
使用自带算法(可以实现整数规划)
使用于2019D 选取片段 每一段为一个决策变量 是否选中为0或1 实则为非线性整数规划 -> 决策变量直接构成染色体 使用ga()求解 目标函数 约束条件参考非线性(G12)
D:\00000MCM\0 codes\2019Dsum\ q3.m主程序 q3_fun.m目标函数 q3_yueshu约束
基于MATLAB的遗传算法使用浅谈 - 知乎(参考)
Find minimum of function using genetic algorithm - MATLAB ga - MathWorks 中国(参考)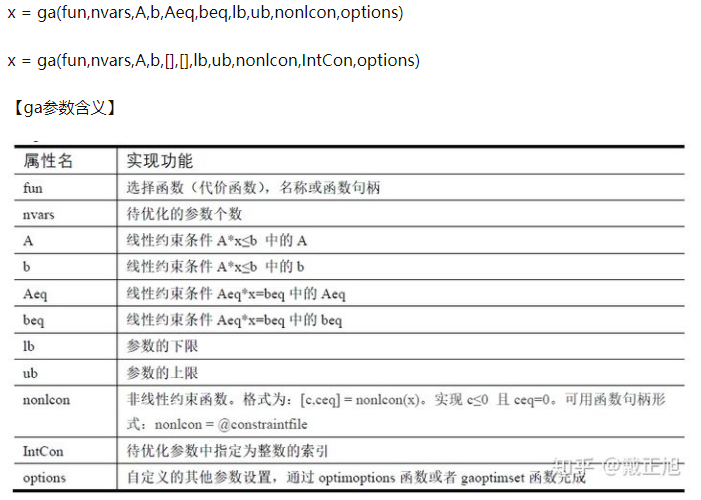
[x,fval,exitflag,output,population,scores] = ga()
x 最优解
fval 最优适应度值
exitflag 结束标志
output 结构体 内容
population 种群 ?行个体 * ?特征
scores 每个个体适应度
遗传算法(Genetic Algorithm, GA)及MATLAB实现 - 午夜的行人 - 博客园
【GA算法】遗传算法原理及其Matlab代码小白兔de窝-CSDN博客遗传算法matlab程序
q3.m主程序 q3_fun.m目标函数 q3_yueshu约束
clearclcload('q3')%%% [x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)global dataglobal okx0 = ones(1, 40);A = [];b = [];Aeq = [];beq = [];lb = zeros(1, 40) - 0.0000001;ub = ones(1, 40) + 0.000000;% [x,fval] = fmincon(@q3_fun,x0,A,b,Aeq,beq,lb,ub,@q3_yueshu) % 规划 无效% x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)[x,fval] = ga(@q3_fun, 40, A, b, Aeq, beq, lb, ub, @q3_yueshu, [1:40])
function f = q3_fun(x)f = 0;flag = 0;global dataglobal oktmp = -10 * ones(1, 21);for i = 1:40if x(i) == 1if flag == 0tmp = data(i, :);flag = 1;elsetmp = [tmp; data(i, :)];endendend% if flag == 0% tmp = -10 * ones(1, 21);% endtmp = mean(tmp, 1);for i = 4:14f = f + abs(ok(i) - tmp(i));end% fend
function [c,ceq] = q3_yueshu(x)jiange = 0;global datafor i = 1:40if x(i) == 1jiange = jiange + data(i, 4);endend% jiangec = [jiange - 1300;1150 - jiange];ceq = [];end
Python
GitHub - guofei9987/scikit-opt: Genetic Algorithm, Particle Swarm Optimization, Simulated Annealing, Ant Colony Optimization Algorithm,Immune Algorithm, Artificial Fish Swarm Algorithm, Differential Evolution and TSP(Traveling salesman)
文档
等式 不等式约束
差分进化算法解决有约束优化问题(Python实现)_guofei9987的博客-CSDN博客
sko.GA实现遗传算法的源码解析_tommy2005的专栏-CSDN博客
七种启发式算法 - 知乎
D:\00000py\1\mcm jupytertest3.ipynb
D:\00000py\1\mcm jupytertest2.ipynb
#%% 初始化%matplotlib inlineimport numpy as npfrom sko.GA import GAimport pandas as pdimport matplotlib.pyplot as pltprint('start')#%% 定义函数def schaffer0(p):'''This function has plenty of local minimum, with strong shocksglobal minimum at (0,0) with value 0'''x1, x2 = px = np.square(x1) + np.square(x2)return 0.5 + (np.square(np.sin(x)) - 0.5) / np.square(1 + 0.001 * x)# + x1 * x2 + x1def schaffer(p):x1, x2, x3, x4, x5 = pans = x1**2 + x2**2 + x3**2 + x4**2 + x5**2 + 1.0return ansnarvs = 5 # 变量个数lbs = [-10] * narvs # 下届 包含等于ubs = [10] * narvs # 上届 包含等于# precisions = [1, 2, 1, 1, 1e-7] # 指定间隔 整数 间隔1 间隔2 浮点数间隔1e-7precisions = [1, 1, 1, 1, 1] # 指定间隔 全整数规划 01规划修改上下界# 遗传算法ga = GA(func=schaffer, n_dim=narvs, size_pop=50, max_iter=800, prob_mut=0.001, lb=lbs, ub=ubs, precision=precisions)best_x, best_y = ga.run()print('best_x:', best_x, '\n', 'best_y:', best_y)# 画图Y_history = pd.DataFrame(ga.all_history_Y)fig, ax = plt.subplots(2, 1)ax[0].plot(Y_history.index, Y_history.values, '.', color='red')Y_history.min(axis=1).cummin().plot(kind='line')plt.show()print('finish')

