本文档是对课程内容的简单整理。

  • 前缀Z_ 为正课视频的简称，如Z1为正课视频第1课
  • 前缀G_ 为更新视频的简称，如G1为更新视频第1课

因子分析法通过研究变量间的相关系数矩阵，把这些变量间错综复杂的关系归结成少数几个综合隐私，这种方法比主成分分析更容易解释

文章
2018C
（用于回归）
D:\00000MCM\0 研究生数学建模竞赛历年真题和优秀论文集锦\研究生数学建模-优秀论文\2020年优秀论文\B20102520228.pdf

（因子分析不建议用于评价）
D:\00000MCM\0 研究生数学建模竞赛历年真题和优秀论文集锦\研究生数学建模-优秀论文\2018\C题
文章 3 5

SPSS 降维 - 因子

  • 统计描述：变量信息
  • KMO 巴特利特检验
  • 总方差解释：左两列 未旋转； 右列旋转后
    • 方差百分比：累计方差贡献率（旋转后 累计方差贡献率作为因子得分权重）
    • 累计：累计（累计值不会变）
  • 碎石图：用于选择因子个数
  • 旋转后成分矩阵：分析解释因子
  • 成分得分系数矩阵：计算FAC（使用标准化后的变量）SPSS已经计算
  • 计算得分：FAC*旋转后方差百分比 / 除以旋转后方差百分比之和 - 排序

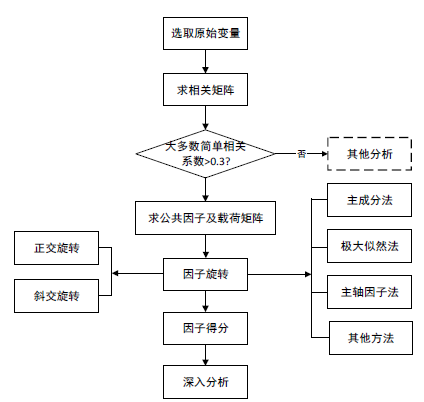
原理

因子分析是一种多元统计分析方法，核心思想是数据变换与降维，先把错综复杂的变量综合成少数主要因子， 再 进行问题解释或综合评价 [ 8]，它可用少量潜在因子解释原始变量大部分信息 [。因子分析的出发点是原始变量的相关矩阵。因子分析可消除变量间的相关性，通过把恐怖袭击风险指标进行数学变换，综合成几个因子，根据一定标准选取主因子，得到每个恐怖袭击事件危害程度综合得分；同时因子不需要主观确定指标权重，而是根据样本数据的观测值自动得到权重，因此可以消除主观因素，提供客观的评价结果。
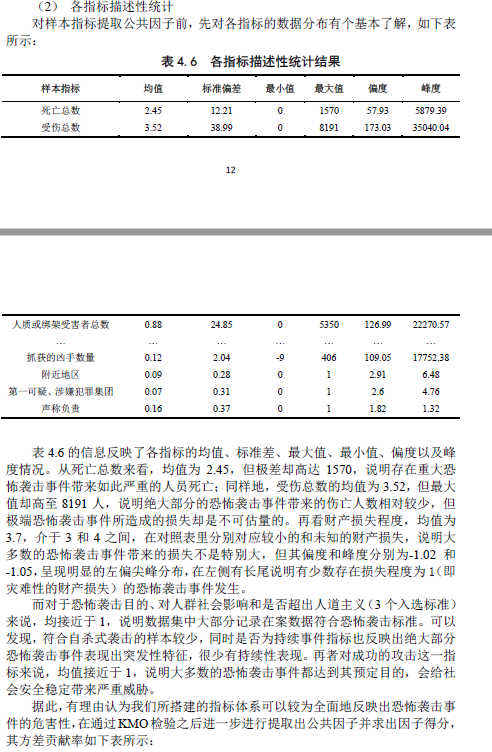
image.pngimage.png
image.png

1 描述统计

image.png

2 Barlett 球形检验 KMO

Barlett 球形检验表明：Bartlett 值为735814，P 接近于0，若显著性水平为0.01，则拒绝相关矩阵为单位矩阵的原假设，相关矩阵与单位矩阵存在显著差异故考虑进行因子分析。取样足够的Kaiser-Meyer-Olkin 检验是用于比较观测相关系数值与偏相关系数值的一个指标，其值越逼近1，表明对这些变量进行因子分析的效果越好。从表4.5 可见，KMO 值为0.672，因而可以对指标变量进行因子分析。

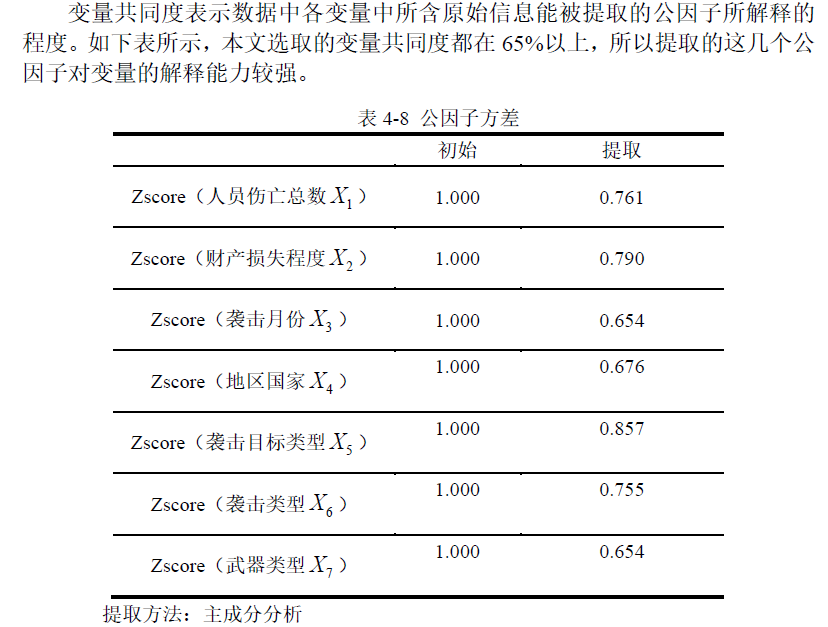
3 公因子方差

image.png

4 总方差解释表 碎石图 -> 选择多少个因子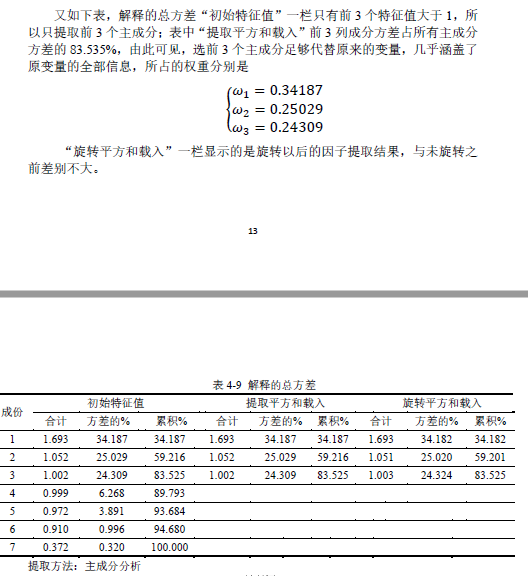
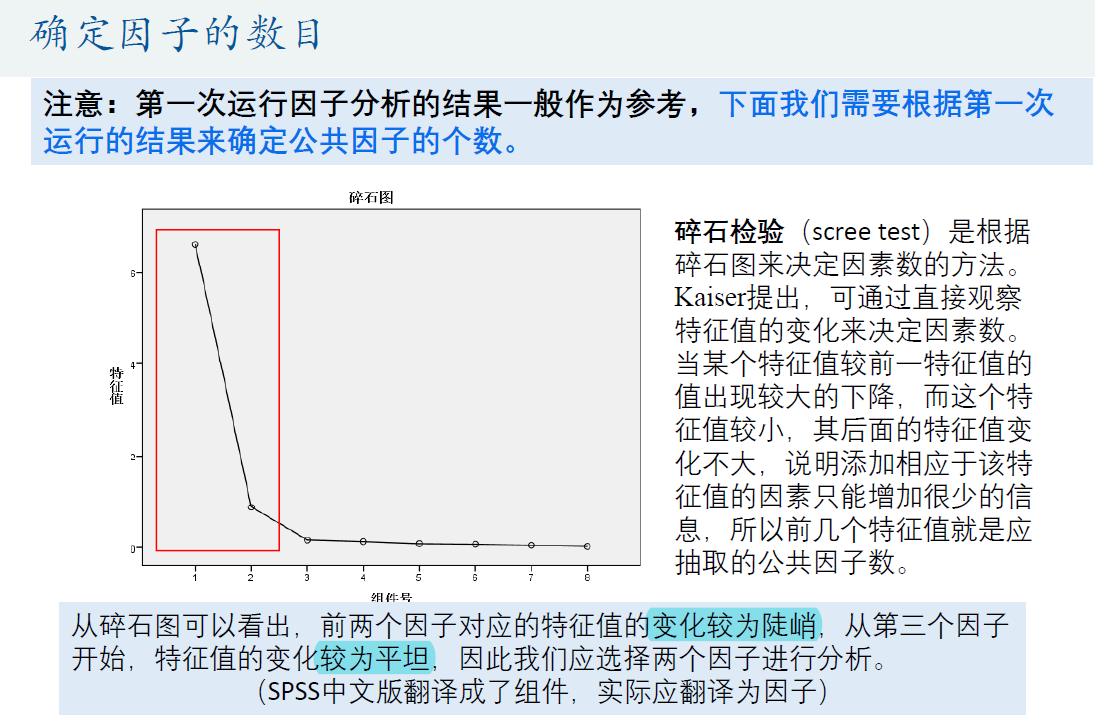
image.png
image.png
image.png
image.png

4 旋转的成分矩阵 -> 定义因子

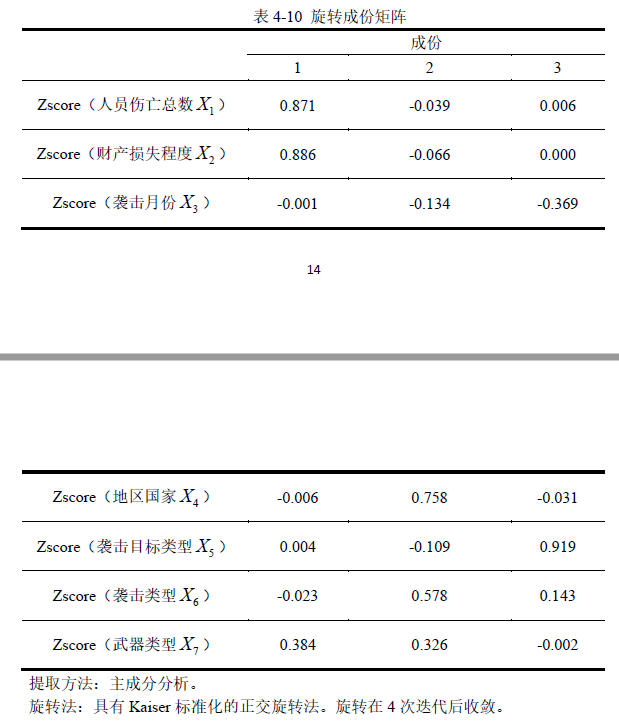
image.png
image.png
image.png

5 载荷图

2 3 维画图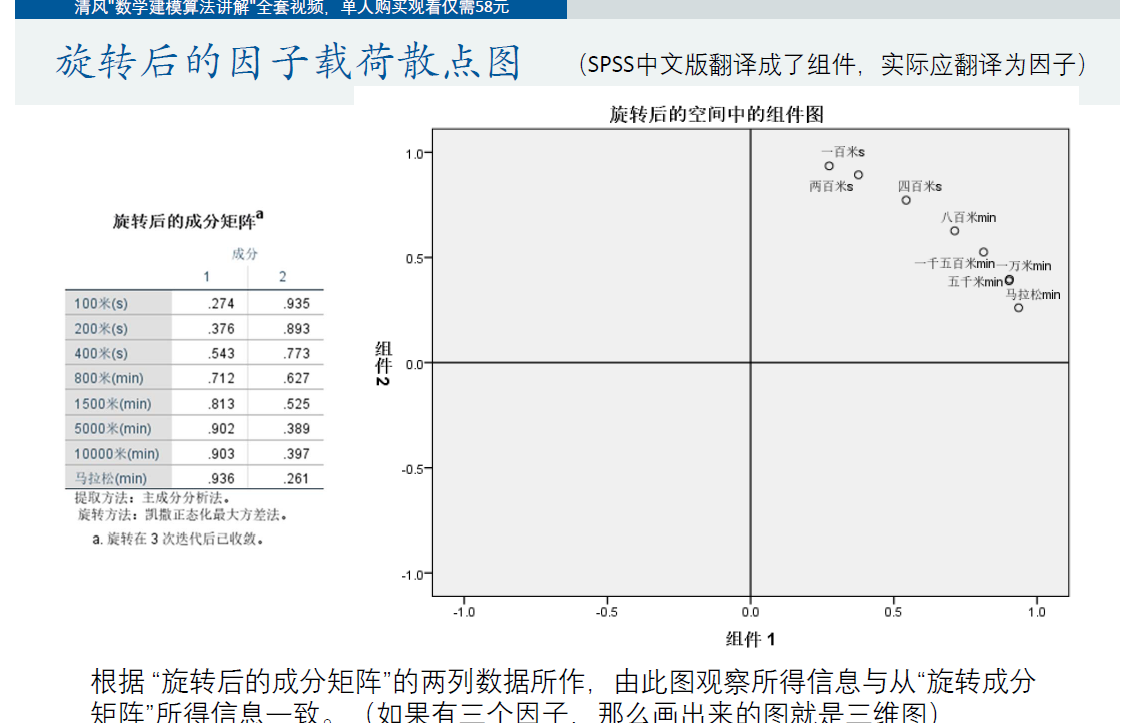
image.png

6 计算因子得分（SPSS已经计算）

计算FAC（使用标准化后的变量）SPSS已经计算

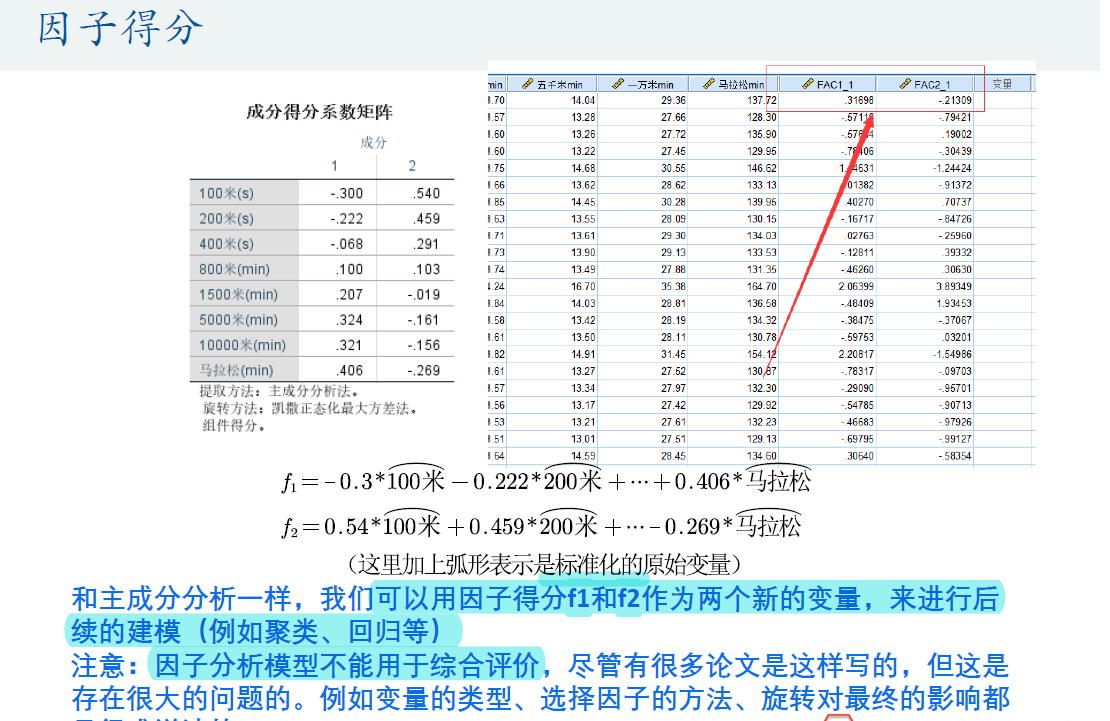
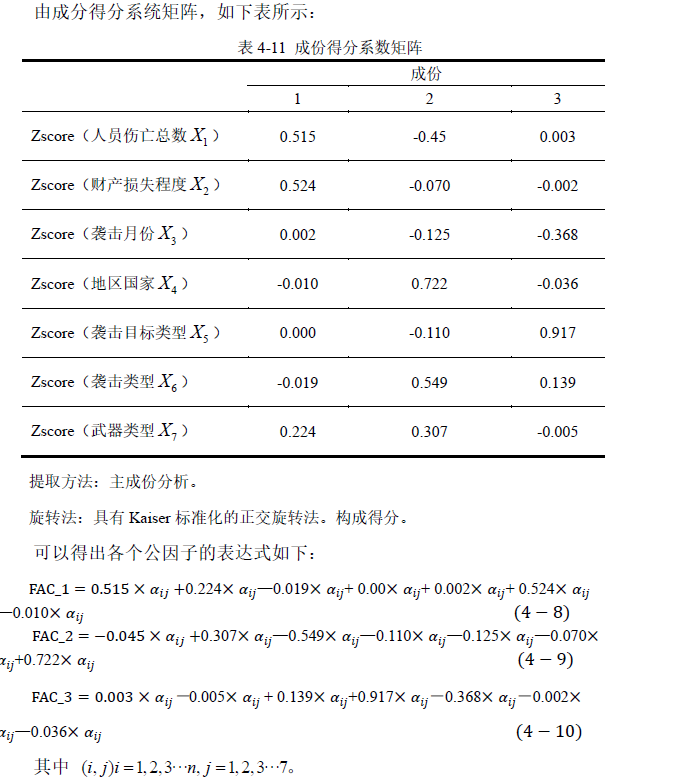
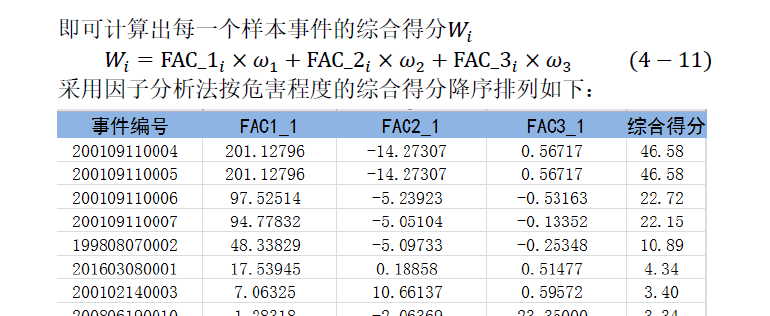
image.png
image.png

7 计算个案得分（手动计算 用于评价）

计算得分：FAC*旋转后方差百分比 / 除以旋转后方差百分比之和 - 排序
image.png