Author: Xingguang Zhong, Yuwei Wu, Dong Wang, Qianhao Wang, Chao Xu, and Fei Gao
Publisher: ICRA
Publish year: 2021
Editor: shirley
Last edit: 2020.11.3

_

Abstract/摘要

本文提出了一种从复杂障碍环境高效地生成大型,无障碍的凸包空间的方法.该空间由点云直接生成,避免复杂计算和点云处理,非常适合嵌入式平台.

Instruction/介绍


III.凸包的生成

定义:
Generating Large Convex Polytopes Directly on Point Clouds - 图1 查询坐标
Generating Large Convex Polytopes Directly on Point Clouds - 图2无序点云
目的是从Generating Large Convex Polytopes Directly on Point Clouds - 图3生成一个不包含Generating Large Convex Polytopes Directly on Point Clouds - 图4中任何点的大型凸包,步骤如下:
1.从无序点云Generating Large Convex Polytopes Directly on Point Clouds - 图5中生成不包含任何点的星型凸多面体
2.调整星型凸多面体为严格的凸包空间

A.生成无点区域

以往我们采用raycasting或三维重建的方法从点云描述环境.对于无序点云,这些方法需要较大的计算量和存储空间.因此避免使用近邻搜索,法向量计算和其他复杂操作使我们的方法更快更轻量级.
设查询坐标Generating Large Convex Polytopes Directly on Point Clouds - 图6为原点,使用球面翻转非线性映(下式)射将Generating Large Convex Polytopes Directly on Point Clouds - 图7中每个Generating Large Convex Polytopes Directly on Point Clouds - 图8变为Generating Large Convex Polytopes Directly on Point Clouds - 图9
Generating Large Convex Polytopes Directly on Point Clouds - 图10(1)
由(1)可知:
Generating Large Convex Polytopes Directly on Point Clouds - 图11(2)
Generating Large Convex Polytopes Directly on Point Clouds - 图12是二范数,R是用户定义的球半径.如图1所示,球面翻转映射将球中的点沿Generating Large Convex Polytopes Directly on Point Clouds - 图13射线映射到球外.
Generating Large Convex Polytopes Directly on Point Clouds - 图14是范数的递减函数，这意味着离查询坐标点越近，它将被映射得越远。因此,可以用该映射将球内和球外的点做翻转.翻转后的点云Generating Large Convex Polytopes Directly on Point Clouds - 图15,逆映射如下:
Generating Large Convex Polytopes Directly on Point Clouds - 图16(3)
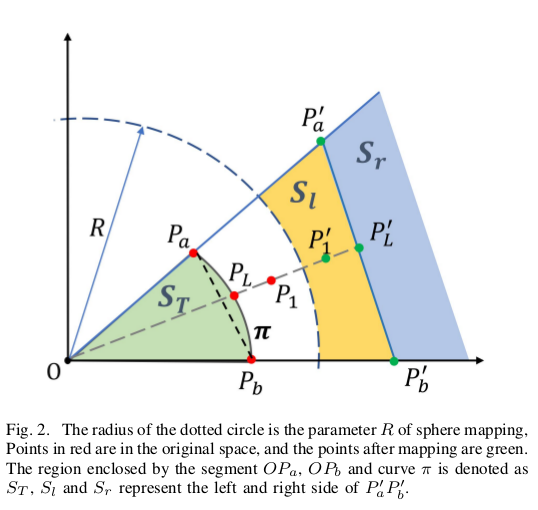
为了方便理解,我们在2维空间描述.如图2,给出两个点Generating Large Convex Polytopes Directly on Point Clouds - 图17.球面翻转后得到点Generating Large Convex Polytopes Directly on Point Clouds - 图18.根据公式3逆映射线段Generating Large Convex Polytopes Directly on Point Clouds - 图19上的点到原始空间,生成一个朝向Generating Large Convex Polytopes Directly on Point Clouds - 图20的曲线Generating Large Convex Polytopes Directly on Point Clouds - 图21.Generating Large Convex Polytopes Directly on Point Clouds - 图22的形状被半径R影响,在[13]中有详述.假设Generating Large Convex Polytopes Directly on Point Clouds - 图23空间中的点Generating Large Convex Polytopes Directly on Point Clouds - 图24,Generating Large Convex Polytopes Directly on Point Clouds - 图25是Generating Large Convex Polytopes Directly on Point Clouds - 图26y与Generating Large Convex Polytopes Directly on Point Clouds - 图27交点,所以Generating Large Convex Polytopes Directly on Point Clouds - 图28是Generating Large Convex Polytopes Directly on Point Clouds - 图29上一点.根据球体翻转递减原理,Generating Large Convex Polytopes Directly on Point Clouds - 图30,那么Generating Large Convex Polytopes Directly on Point Clouds - 图31在Generating Large Convex Polytopes Directly on Point Clouds - 图32范围以外.
同理Generating Large Convex Polytopes Directly on Point Clouds - 图33是Generating Large Convex Polytopes Directly on Point Clouds - 图34的映射.在射线Generating Large Convex Polytopes Directly on Point Clouds - 图35范围内,Generating Large Convex Polytopes Directly on Point Clouds - 图36中没有点,那么三角形Generating Large Convex Polytopes Directly on Point Clouds - 图37也是空的.
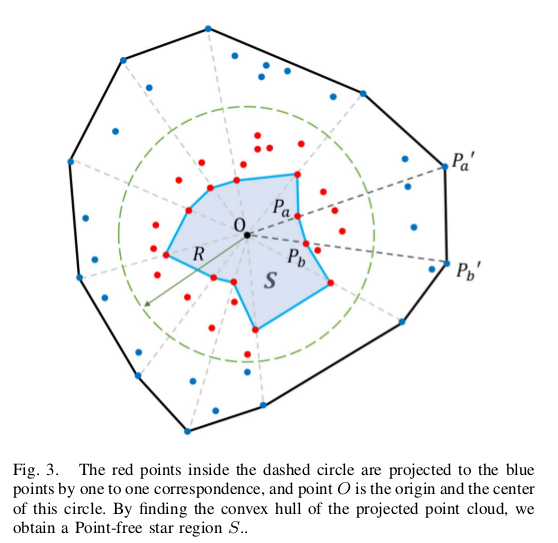
image.png
如图3所示,给出查询点Generating Large Convex Polytopes Directly on Point Clouds - 图39和原始点云图.
假设没有穿过Generating Large Convex Polytopes Directly on Point Clouds - 图40的超平面可以让所有其他点都在Generating Large Convex Polytopes Directly on Point Clouds - 图41的同一侧，这意味着Generating Large Convex Polytopes Directly on Point Clouds - 图42点被点云包裹.
采用[14]著名quick-hull[wiki]QuickHull.pdf算法找到凸包点.Generating Large Convex Polytopes Directly on Point Clouds - 图43是两个相邻顶点,逆映射到原始点云中为Generating Large Convex Polytopes Directly on Point Clouds - 图44,根据球体翻转属性,在线段Generating Large Convex Polytopes Directly on Point Clouds - 图45右侧没有点,那么三角Generating Large Convex Polytopes Directly on Point Clouds - 图46中没有点.最终组合所有边对应的三角区生成空的区域Generating Large Convex Polytopes Directly on Point Clouds - 图47.

image.png
定理1:区域Generating Large Convex Polytopes Directly on Point Clouds - 图49是星型凸多面体.
证明:略

B.调整为凸包

给出一种高效的将星型凸多面体调整为凸包的方法
凸多面体表达式:
Generating Large Convex Polytopes Directly on Point Clouds - 图50
Generating Large Convex Polytopes Directly on Point Clouds - 图51矩阵, Generating Large Convex Polytopes Directly on Point Clouds - 图52向量, Generating Large Convex Polytopes Directly on Point Clouds - 图53
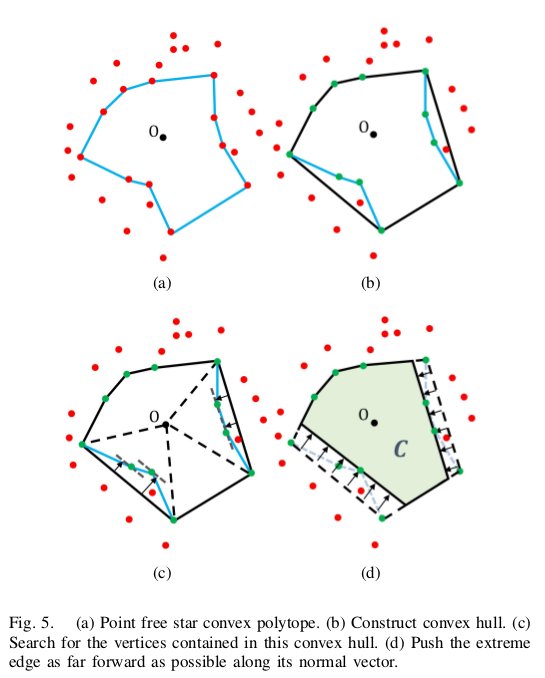
image.png
如图所示,
1.将凸多面体调整为凸壳H,H中会包含障碍点
2.将选择所有H内的点,并且将凸壳的边平移到距离凸壳最远的点上,得到无障碍凸包C
伪代码如下:
image.png
该方法不能保证获取最大的凸包区域,由于边的数量较少,实际实验中计算时间不超过0.5毫秒.
该算法简单高效,计算量最大的过程是球体翻转后的凸壳构建.在2D或3D场景,convex hull algorithm的平均复杂度是nlog(n).
源代码在论文接收后会在https://github.com/ZJU-FAST-Lab/Galaxy给出.

IV.评估

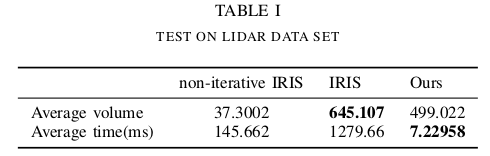
为了验证算法性能,我们使用真实环境的雷达点云数据测试算法.和IRIS算法比较生成凸包的体积及运行时间.IRIS是替代方法,过程如下:

A.使用雷达数据集测试
SLAM框架使用LIO-SAM,目的是验证算法可以在复杂环境下的范围传感器中应用.设置边界为Generating Large Convex Polytopes Directly on Point Clouds - 图56,运行结果如下:凸包大小比IRIS小22%,计算时间只占IRIS的0.6%.
image.png