| Author: | Xin Zhou, Zhepei Wang, Chao Xu and Fei Gao |
|---|---|
| Publisher: | Robotics |
| Publish year: | 2020 |
| Editor: | 李笑莹 |
| Last edit: | 2020-10-18 |
Abstract/摘要
基于梯度的planner算法被用于四旋翼局部规划,ESDF是计算梯度方向幅值的关键。在轨迹优化生成时只更新到ESDF的有限空间,大部分空间的计算都是冗余的。本文中,提出了一种ESDF-free基于梯度的planning框架,能够显著减少计算量。对于碰撞阶段,对碰撞轨迹和无碰撞的引导轨迹进行建模,建立惩罚函数,结果是只有当轨迹碰到新的障碍时,障碍信息才会被存储,使planner只提取关键障碍物信息。然后,如果不满足动力学要求,则我们拉长分配时间。提出了一种曲线适应算法,调整轨迹的高阶导以保证原始形状。基准对比和实验证明了他的鲁棒性和较好的表现,源码以ROS包的形式发布
Instruction/介绍
传统基于梯度的规划依靠提前建好的ESDF地图评估梯度大小和方向,用数值优化生成局部最优解。在EWOK中ESDF计算占据70%的运行时间。如图1,在资源有限的平台下,建立ESDF已经成为梯度优化方法的瓶颈。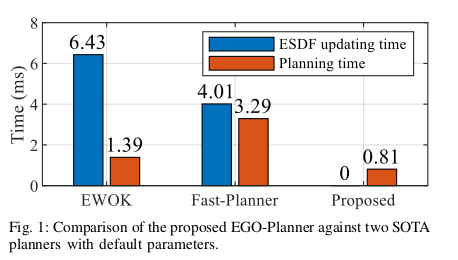
有两种方法建立ESDF地图,在第二章详述。大致分为增量式全局更新,和批量局部更新。但它们都并非专注于轨迹本身。由于太多计算资源用于计算ESDF值,以至于对planning毫无贡献,基于ESDF的方法并不是单独直接地服务于轨迹优化。
如图二,对于自主导航场景,无人机期望局部避障,轨迹只覆盖到ESDF更新的小范围内。在实践中,即使可以人工制定规则来决定ESDF的范围,但它们缺少理论支持且仍会产生不必要的计算
,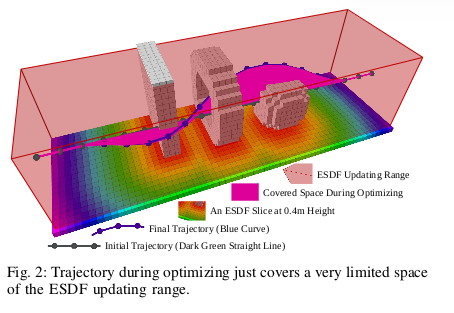
在本文中,我们设计了一个ESDF-Free的基于梯度的局部规划框架EGO,并且我们慎重考虑工程需要,使它轻量化和鲁棒性。提出的算法由基于梯度的样条优化和后细化程序组成。首先,我们优化轨迹基于平滑,避障和动态可行性。与传统构建ESDF方法不同的是,collision cost 模型是计算在障碍物内部的轨迹与无碰撞的引导路径之间的差。我们生成一个力作用于碰撞轨迹到障碍之外。在优化过程中,轨迹将在障碍附近回弹几次最终在安全区域内。 用这种方法我们只需要在需要的时候计算梯度,避免在与局部轨迹不相干的区域计算ESDF。如果轨迹违反动力学限制,通常由于不合理的时间分配导致,在重优化过程调整。在重优化时,轨迹时间被重新分配以满足动力学要求。增大时间分配后,新的B样条满足之前的动力学要求并且平衡动态性能和精度。为了提高鲁棒性,拟合精度是各向异性建模的,在轴向和径向上有不同的惩罚。
这是第一个ESDF-free的基于梯度的局部规划方法,对比当前最新的工作,提出的方法生成了安全,平滑,激进的轨迹,而且通过省略ESDF维护,将计算时间缩短了一个数量级。经过仿真和实验验证。本文的贡献是:
1.提出了新型鲁棒的基于梯度的局部规划方法,计算生成梯度信息直接来自障碍而非预先建立的ESDF
2.提出了一个轻量级高效的轨迹重优化算法,生成更平滑的轨迹,通过各向异性误差补偿解决轨迹拟合问题
3.整合提出的方法到完整的自主四旋翼系统,并且发布软件
Related Work/相关工作
1.基于梯度的运动规划
基于梯度的运动规划是无人机运动规划的主流,建立非线性优化模型。ESDF首先被Ratliff提出用于机器人运动规划。利用他的梯度信息,许多规划框架在configuration space直接优化轨迹。然而,在离散时间内优化轨迹不适用于无人机,因为它对动力学约束更敏感,因此为无人机规划提出一个连续时间的多项式轨迹优化方法。然而,涉及到势场函数的计算产生了沉重的计算负担。此外这种方法的成功率只有70%,甚至会随机重启。对于这些缺点[2]介绍了B-spline参数化轨迹,利用其凸包特性。在[8]中,在前端找到安全路径并初始化能够显著提高成功率,在[9,10]中加入动力学约束后,表现更好。融合感知使系统更有鲁棒性。上述这些方法,ESDF在近障碍时计算带有梯度信息的距离有重要作用
2.欧式距离场(ESDF)
ESDF被用于从有噪声的传感器中三维重建物体已有20多年[12],并且从[5]后被机器人运动规划重燃热情。
略
III.估计避障的力
本文中,待优化的量是B-spline曲线的控制点Q,每个Q独立拥有它自身的环境信息,在每次 迭代中计算其排斥力。
以前,一个原始B样条曲线不考虑障碍满足给出的约束,然后优化程序启动。在一次迭代中对每个碰撞轨迹段检测,产生一个无碰撞路径
。碰撞轨迹段的每个控制点
会被分配一个在障碍表面的锚点
和相应的排斥方向矢量
,如图4(a),其中
控制点索引,
是
的索引。注意
只属于一个特殊控制点。
生成的详细过程和描述在算法1和图4b。生成
后,从控制点
到障碍物距离被定义如下
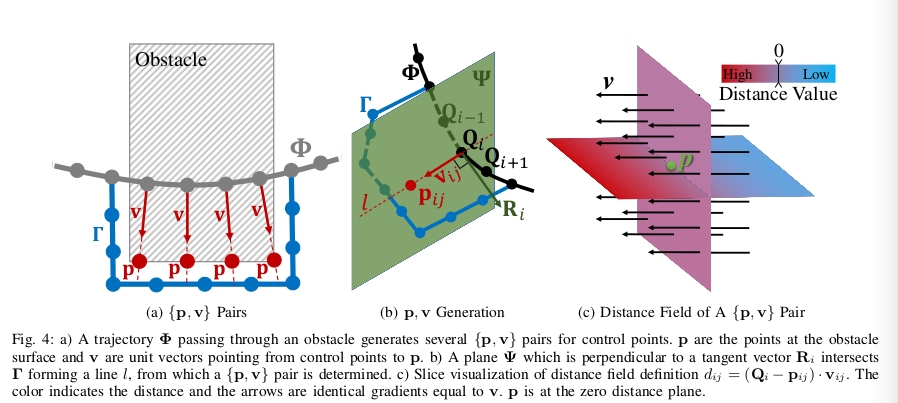
为了避免在轨迹远离障碍的前几次迭代时生成重复的,我们应用一个标准,当一个在障碍中的控制点第一次被发现时,这个控制点对所有的
满足
。此外,该标准只允许必要的障碍在最终轨迹优化中起作用,因此,运行时间大大减小。
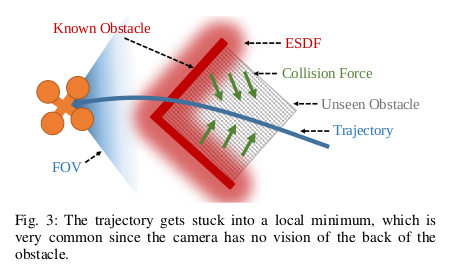
为了在局部规划中融合必要的已知环境信息,我们需要显式构造一个目标函数,使轨迹远离障碍物。ESDF提供重要的障碍信息但是对计算量要求有沉重负担。此外,如图3,基于ESDF的规划容易陷入局部最优而使远离障碍失败,因为从ESDF中获取不充分或错误的信息。为了避免这种情况,前端需要提供一个安全无障碍的初始路径。上述方法胜过用ESDF提供障碍物排斥力信息,因为精确设计的斥力对于各种任务和环境可能相当有效。此外,本文方法不需要安全无障碍的初始化路径。
IV.基于梯度的轨迹优化
A.问题模型
本文中,轨迹被参数化为均匀B样条曲线,唯一地由阶次
,
控制点
,和节点向量
,其中
,
,
。由于轨迹的简单和效率性要求,我们采用均匀B样条,意味着在运行中每个节点被分成相同的时间间隔
。本文中问题模型是基于最新的四旋翼局部规划框架FAST-planner。
B样条有凸包特性,这个特性表明每段B样条仅由个连续控制点控制,且在控制点构成的凸包内。例如在
时间内的线段位于
形成的凸包内。另外一个特性是一个B样条的
阶导是一个次数为
的B样条。由于一条轨迹
的
相同,控制点的速度
,加速度
,加加速度
曲线如下:
(2)
我们根据[15]的工作在微分平坦空间内规划控制点,建立优化问题模型如下:
(3)
其中,
分别是其权重。
1)平滑性惩罚:考虑无时间积分的加速度和加加速度的平方惩罚。公式如下: (4)
2)碰撞惩罚函数:碰撞惩罚函数将控制点推离障碍,使用安全间隙,惩罚
的控制点。为了进一步促进优化,我们构建了二次连续可微分的惩罚函数
,并且在
减小时抑制斜率,分段函数如下:
(5)
由
对应的
生成,每个
的cost独立计算且从对应的
累计.因此,如果发现更多障碍物,则控制点将获得更高的轨迹变形权重。(Tips:一个
可以对应多个
),对于一个控制点,其cost是该控制点对应所有锚点cost的和,即
,
是属于
的锚点个数.
是所有控制点cost和,即
(6)
不同于传统基于ESDF采用三线性插值求梯度的方法[2,10],我们直接通过对微分求梯度.如下:
(7)
3) 可行性惩罚:可行性惩罚有每个维度轨迹的高阶微分约束.,
表示每个维度.由于凸包特性,约束控制点的导数足以约束整个B样条。因此,可行性函数如下:
(8)
是每项的权重,
是控制点高阶导的二阶连续可微函数.
(9)
(10)
其中被选择满足二阶连续,
是导数极限,
是三次区间和二次区间分割点,
是弹性系数
使结果满足连续性,因为代价函数是各权重的平衡.
B.数值优化
本文中的问题有两方面,一是目标函数J根据新发现的障碍自适应调整,它需要求解器快速计算重新开始.二是目标函数主导项为二次,可以近似J为二次.这意味着利用Hessian信息可以显著加速计算.然而,获取精确地Hessian逆矩阵由于计算量巨大导致不能保证实时性.为了规避Hessian逆矩阵的计算,采用准牛顿方法从梯度信息近似Hessian逆矩阵.
由于求解器性能取决于问题,我们对比了三种准牛顿算法,分别是1.Barzilai-Borwein,该方法通过在给定状态添加轻微扰动来估计Hessian矩阵.2.L-BFGS方法[18]可以从先前的目标函数评估中近似Hessian,但需要一系列迭代才能达到相对准确的估计。比较第VI-B章节的状态,L-BFGS在内存占用,Hessian逆矩阵精度和重启损失的平衡相较于其他两种方法表现更突出.简要介绍该方法,对于无约束优化问题,,x更新近似牛顿步长:
(11)
其中是步长,
通过以下公式迭代更新:
(12)
其中
这里计算不精确.该算法公式(12)右乘
,递归拓展m步,然后得到有效的双循环递归更新方法,时间/空间复杂度为线性.Barzilai-Borwein步长权重使用Hessian逆矩阵
初始化,
(13)
强wolfe条件下的单调曲线被用于强制收敛.
V.时间重分配和轨迹重定义
因为规划器不知道最终轨迹信息,所以在优化之前精确分配时间是没有根据的.因此,额外的时间重分配步骤用于保证动态可行性.[9,10]将轨迹参数化为一条非均匀B样条,并且当某路径段不满足速度/加速度等导数限制时,迭代的延长节点的时间跨度.
然而一个节点跨度影响多个控制点,当节点跨度接近开始状态时导致与先前的轨迹高阶不连续.在这个章节,均匀B样条轨迹
通过IV章的安全轨迹
采用时间重分配重新生成,然后,提出了一种各向异性曲线拟合方法,使
自由地优化其控制点,以满足高阶导数约束,同时保持与
几乎相同的形状。
首先,如Fast-Planner[14],我们计算超出范围的比率, (14)
其中其中m代表导数项的范围.
表示我们相对于
,
应当增加多少时间分配.注意从公式2可知,
分别与
成反比例,反平方,反立方关系.然后我们得到
新的时间节点
(15)
为了保证形状和控制点个数,
的新时间节点
由下边界约束初始化,转化为求解闭式最小二成问题.然后平滑性和可行性被重优化.惩罚函数
是平滑性(Sec. IV-A.1),可行性(Sec. IV-A.3)和曲线拟合(稍后介绍)的线性组合,如下:
(16)
其中是拟合项权重.
拟合项惩罚函数表示为从
到相应的
的各向异性位移积分,其中
分别是
轨迹时间.由于拟合曲线
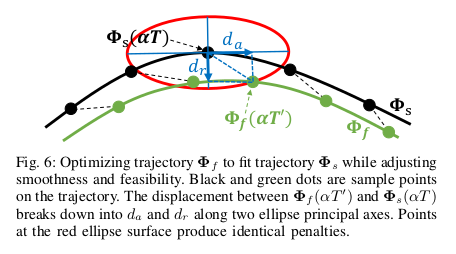
已经无碰撞,我们将两条曲线的轴向位移采用低惩罚权重,以放宽平滑度调整限制,而径向位移则以高惩罚权重来避免碰撞。如图6,用于
的椭球是由以
为圆心的椭圆绕其切线方向(即
)旋转而来,所以轴向位移
和径向位移
计算如下:
(17)
拟合惩罚函数:
(18)
其中a和b分别是椭圆的短半轴和长半轴,该问题用L-BFGS求解.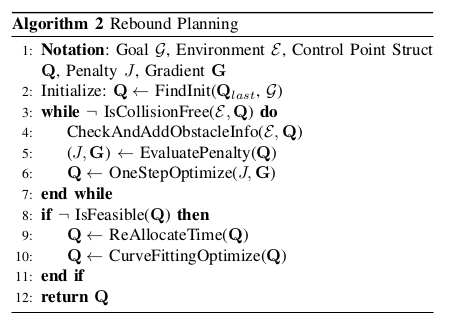
VI.实验结果
A.实施细节
在算法2中总结的规划框架,我们设置B-spline阶数为.对于无碰撞路径搜索,我们采用A*,路径
可以自然的贴近障碍物表面.因此我们直接在
上选择p.对于Fig.4b定义的向量
,利用均匀B-spline参数化性质可知
满足:
(19)
可以快速计算.方程18被离散为有限个点,其中
.为了进一步加强安全性,对最终轨迹固定半径范围内进行碰撞检查。直到检测不到障碍停止该优化.实际实验平台采用[19],带有Intel RealSense
获取深度.此外,我们修改了Intel RealSense的ROS驱动程序,使激光发射器每隔一帧触发一次。这使得该设备可以在发射器的帮助下输出高质量的深度图像,同时还可以输出不受激光干扰的双目图像。修改后的驱动程序也是开源的.
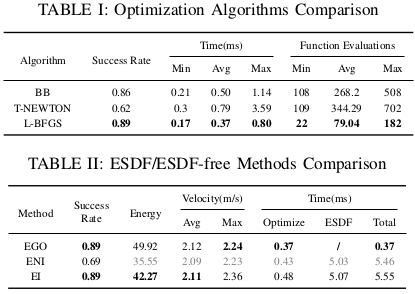
B.优化算法对比
在本节,讨论不同的优化算法Barzilai-Borwein (BB) method, limited-memory BFGS (L-BFGS) and truncated Newton (T-NEWTON) method [17].每个算法独立地在随机地图中跑100次,所有相关的参数,包括边界约束、时间分配、决策变量初始化和随机种子,对于不同的算法都是相同的。数据记录了目标评价函数的成功率、计算时间和次数。由于失败案例中的数据毫无意义,因此只统计成功案例。相关结果在Tab1,L-BFGS显著优于其他两个算法.L-BFGS用二阶泰勒展开描述了一种近似,适用于优化Sec.IV-B的目标函数.截断牛顿法也近似于二阶优化方向。但是,太多的目标函数评估增加了优化时间。BB方法将Hessian估计为一个标量λ乘以I,但由于Hessian估计不充分,收敛速度仍然很低。
C.带有&不带ESDF的轨迹生成
我们使用Sec.VI-B中相同的设置进行比较。鉴于[14]在使用基于ESDF的轨迹生成器进行直线初始化时成功率较低,我们采用无碰撞初始化。比较结果在Tab II.
用EI和ENI分别表示无碰撞初始化和直线初始化.比较表明,所提出的EGO算法与基于ESDF的无碰撞初始化方法的成功率相当。然而,EGO轨迹能量(jerk积分)略高,因为EGO的控制点包含多个{p,v},产生更强的轨迹变形力,如IV-A.2所述。另一方面,更强的力加速收敛过程从而缩短优化时间.与EI和EGO相比,ENI的一些统计数据(以灰色显示)可能不那么令人信服,因为ENI测试只能在较少的挑战性情况下成功,生成的轨迹自然更平滑,能耗更低,速度更低。值得注意的是即使ESDF更新范围减小到像素对于9m长的轨迹,ESDF更新仍然占用了大部分的计算时间.
D.规划对比
我们对比了Fast-Planner 和 EWOK两种利用ESDF估计障碍距离和梯度的方法,每个规划器从相同的开始到结束运行10次不同的障碍物密度。平均性能统计信息和ESDF计算时间Tab.III,Fig.1。在的地图上,三种方法生成的轨迹如Fig.8所示。

从Tab.III我们的结论是,与Fast-Planner相比,所提出的方法可以获得更短的飞行时间和轨迹长度,但最终会产生更高的能量成本。搜索路径主要是由前端动力学路径搜索[14]引起的。在稠密环境下,由于目标函数包含指数项,所以EWOK的轨迹是曲折的,导致优化过程中收敛不稳定。此外,在不进行ESDF更新的情况下,该方法节省了大量的计算时间。
E.Real-world Experiments
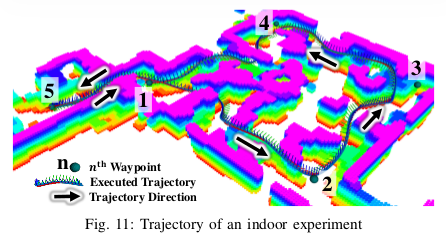
我们在复杂未知环境使用有限的视场角FOV进行多次实现,一次实验是给前方一个点飞行,在本次试验中,无人机从一个小办公室为起点,通过门,在一个乱七八糟的大房间里然后返回办公室,如图10a和图11.室内实验最窄的通道小于1m如Fig.7所示,飞机在该复杂环境速度达到3.56m/s.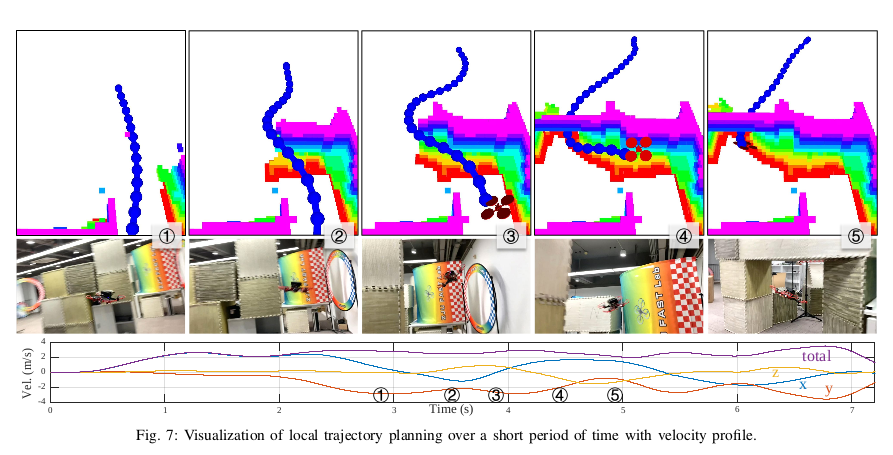
另一个室内实验是在飞行过程中任意地、突然地给出目标,如图10c所示。在本次试验中,有限的视野带来了更大的挑战,即一旦收到新目标或检测到碰撞威胁,必须立即生成可行的轨迹。因此,本实验在可行性的前提下,验证了所提出的规划器能够进行激进地飞行。
在室外实验中,无人机在一片茂密的树木和低矮的灌木丛中飞行,如图10b和图9所示。尽管无人机周围的气流会引起树枝和树叶的摆动,使地图不太可靠,但无人机的速度仍能达到3m/s以上。因此,所提出的规划器可以同时处理实验和野外环境。我们建议读者参考视频3了解更多信息。

VII.结论和未来工作
本文提出了一种无ESDF的局部规划器。它的性能可与一些最先进的基于ESDF的规划器相媲美,但将计算时间缩短了一个数量级。通过基准比较和实际实验验证了该算法的鲁棒性和高效性。
该方法还存在一些缺陷,即A*搜索引入的局部最小值和统一时间重新分配引入的保守的轨迹。因此,我们将致力于通过反转向量v和寻找新的对应点p来执行拓扑规划,这将导致多个轨迹候选,从而帮助逃避局部最小值。然后,我们将重新制定轨迹的终端约束,以规避时间重新分配问题,并尝试生成时空最优轨迹。所有改进都将是轻量级.