| Author: | Zhepei Wang, Xin Zhou, Chao Xu, Jian Chu, and Fei Gao |
|---|---|
| Publisher: | IEEE Robotics and Automation Letters (RA-L) |
| Publish year: | 2020 |
| Editor: | shirley |
| Last edit: | 2021-02-01 |
Abstract/摘要
在本文中提出了一个框架,能够计算大量激进的多项式轨迹,计算高效且带有时空优化.
- 利用规划问题的隐式分离结构,在边界条件和轨迹段的时间片段之间进行交替最小化。
- 利用子问题的代数特性逃离局部最小,降低计算时间.
- 提出了该方法全局/局部收敛率的理论分析。
- 此外,基于多项式理论,为各种约束设计了一种极快的可行性检查方法。
- 通过将该方法融入交替结构,在可行性的前提下构建了约束最小化算法,以优化轨迹。
结果: 在效率,优化结果和可拓展性上比最新的方法表现要好.在有限空间和密集障碍物的侵略性飞行实验中,演示了该算法的性能。
Instruction/介绍
大多数基于线条的优化方法只采用简单的时间优化,规划出来的轨迹过于保守,并且非线性求解器无法求解时间空间耦合问题.我们提出了一种交替求解空间和时间优化问题的框架,能够在一毫秒内得到轨迹优化结果.我们的方法的原理是,具有奇数阶次的多项式轨迹可以由其端点导数(即边界条件和持续时间)唯一确定。对于分段多项式,每段轨迹仅依赖于其时间分配,因此可以分别进行优化.利用线性二次优化求时间分配问题.此外采用闭式解的方法对航点上的导数进行更新。基于上述结果,可以通过交替最小化 (AM) 过程高效处理中间点优化.
- 提出了一种无约束的交替最小化算法,以有效地生成时空最优轨迹,并验证了全局/局部收敛。
- 为各种约束设计了一种极快的可行性检查方法。
- 构建了约束交替最小化算法,以递归方式优化可行轨迹,并验证了全局收敛。
- 该方法被集成到一个自主的四旋翼系统中,然后由实际实验和广泛的基准进行评估。源代码发布github参考。
章节安排:第二节讲述相关文献,第三节讲述预备知识,第四节和第五节分别详细讲述无约束的时空轨迹生成方法和约束条件.第六节展示实验和评估结果,第七节为本文结论.
RelatedWork/相关工作
略
Preliminaries/预备知识
1.微分平坦:四旋翼的轨迹规划只能在平移空间中完成。
2.动力学可行性可隐式地转化为轨迹平滑性.
3.然后,可以通过限制高阶导数的模来实施电机约束。
本文中,每段轨迹用N阶多项式表示:
我们只考虑奇数阶次多项式,因为N为奇数时,待定系数个数和已知边界条件的个数相等.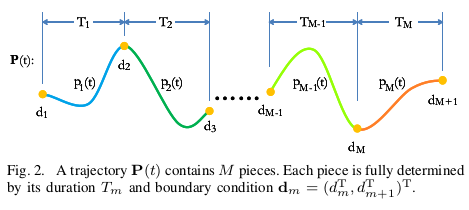
path simple algorithm:Ramer-Douglas-Peucker-Algorithm

