| Author: | Daniel Svensson |
|---|---|
| Publisher: | IEEE/2019 Sensor Data Fusion: Trends, Solutions, Applications(SDF) |
| Publish year: | 2019 |
| Editor: | 柯西 |
Abstract/摘要
用于自动车辆跟踪的运动模型有很多,其中一个是恒定转向速率和加速度(CTRA)模型。在原始雷文中介绍了模型,状态预测方程,但是没有过程噪声,本文中推导过程噪声,此外还推导了离散时间的预测模型,用于线性离散化。
关键字:目标跟踪,传感器融合,运动模型,协方差矩阵,自动驾驶,卡尔曼滤波
Instruction/介绍
自动驾驶系统要对周边环境及交通状况有精确的描述,而环境感知的核心部分是目标跟踪。目标跟踪有两个模块格外重要,一个是运动模型,一个是测量模型。本文论述运动模型。
运动模型是根据物体的当前状态描述其未来状态,是递归滤波器(如卡尔曼滤波)中的预测部分。为了最好的跟踪精度,运动模型需要和被跟踪物体的物理运动一致。运动模型有两个重要部分:预测函数和过程噪声协方差矩阵
当跟踪路上的车辆物体时,最好的运动模型是CT系列模型[4]-[6],这些模型假设物体转向速率为常数,且加入过程噪声扰动。在文献[5]中,对比了不同的CT模型,主要的三个模型如下:
- 恒定转向速率和恒定速度模型(CTRV)
- 恒定转向速率和恒定加速度模型(CTRA)
- 恒定曲率和加速度模型(CCA)
CTRV模型是针对横向转弯,该模型有五维状态量,分别为二维位置量,速度,航向和航向角速度。在该状态量增加加速度,而非假设速度为常数,则得到CTRA模型。CTRV和CTRA都忽略了曲率().CCA模型包括曲率作为状态量。CTRV和CCA模型的集合解释是假设车辆沿圆形轨迹运动,CTRA则假设回旋(clothoid)曲线。
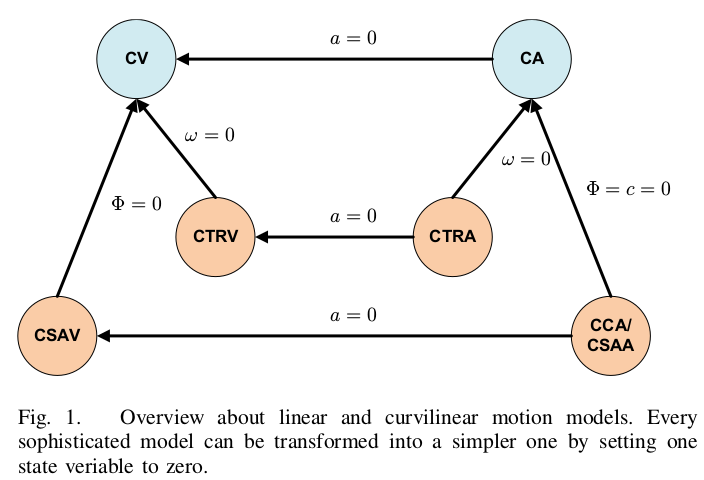
在论文[5]中,使用UKF以GPS和里程计信息为输入,对几个运动模型进行评估。其中表现最好的是CTRA,因此本文主要关注CTRA模型。CTRA过程噪声协方差可以直接应用于CTRV模型,但不适用与CCA。
论文[5]中给出了CTRA运动模型(本文给出的模型与其表达方式不同),但是没有推导过程,且没有给出过程噪声协方差矩阵。在本文中给出了基于白噪声的时间连续运动模型到时间离散的CTRA模型的推导,和过程噪声协方差。
问题描述
一般的带噪声的时间连续非线性运动模型如下,
其中,是预测函数,
是时间连续的过程白噪声向量,矩阵
是过程噪声向量到状态向量的维度映射。CTRA的时间连续的状态向量如下:
其中,是位置的横坐标和纵坐标,
航向,
速度,
加速度,
航向角速度(转向角速率)。

预测函数如下:
加速度和转向角速度近似为零,过程噪声,
分别为jerk和转向角速率噪声的功率谱密度。
本文重点在于离散运动模型的推导
状态向量:
离散时间步长为,
是离散噪声。
离散时间CTRA模型推导
预测函数
对公式(3)中的预测函数进行离散,在论文[9]中,有两种连续时间运动模型线性化和离散化方法,分别为线性离散,和离散线性。第一种方法,非线性时间连续模型先被离散然后用泰勒展开近似,该方法更精确,但只在论文[9]中应用。CTRA模型采用该方法,在拓展卡尔曼滤波(EKF)中,线性化步骤比较重要。对于sigma-point方法,离散预测模型就足够了。
非线性滤波的离散预测步骤在连续时间预测函数中已经给出:
由于噪声均值为0,离散预测函数如下:
离散信号定义如下:
离散时间预测如下:
从角速度和加速度开始,由公式(11)和公式(3),可得:
速度预测公式如下:
航向预测公式如下:
对于横轴位置,有:
用分部积分,得到:
积分上下限展开,如下: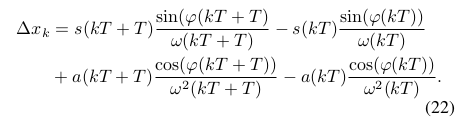
因为,,可得:
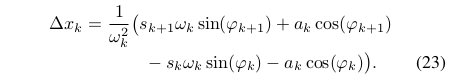
对于纵轴位置,有:
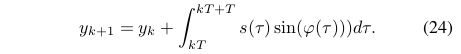
采用分部积分: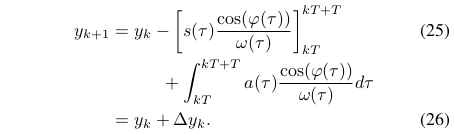
上下限积分展开如下: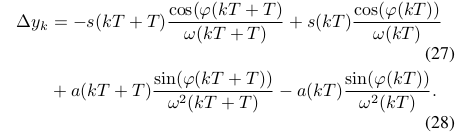
因为,,可得:
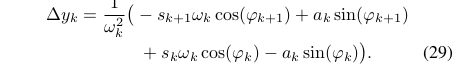
综合以上推导,CTRA运动模型如下:
其中T为一次迭代的时间步长.
过程噪声协方差:
本节推导过程噪声的协方差矩阵.协方差矩阵基于角速度和加速度近似常数的假设,变化量是角速度导数和加速度导数(jerk).过程噪声被参数化为
,分别为角速度和加速度的功率谱密度.
根据文献[9],有五种从连续时间协方差矩阵计算离散时间协方差矩阵的方法.基本假设为是连续白噪声,方差为Q.过程噪声的导数也用该假设.在推导中,我们假设连续时间噪声为高斯白噪声,则离散时间协方差矩阵如下:
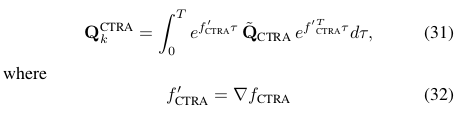
是运动预测模型函数的梯度,
是
的转置
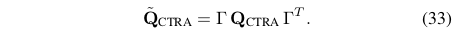
Rreferences:
[1] Y. Bar-Shalom, and X.R. Li, “Multitarget-Multisensor tracking: Princi-ples and Techniques,” YBS Publishing, Storrs, CT, 1995
[2] S. Blackman, and R. Popoli, “Design and Analysis of Modern Tracking Systems,” Artech House, Norwood, 1999.
[3] R.E. Kalman, “A New Approach to Linear Filtering and Prediction Problems,”Transactions of the ASME–Journal of Basic Engineering, 82 (Series D): 35-45, 1960.
[4] F. Gustafsson, and A.J. Isaksson, “Best choice of coordinate system for tracking coordinated turns,” Proceedings of 35th IEEE Conference on Decision and Control, 1996.
[5] R. Schubert, E. Richter, and G. Wanielik, “Comparison and evaluation of advanced motion models for vehicle tracking,” Proceedings of the 11th International Conference on Information Fusion, 2008.
[6] X.R. Li, and V.P. Jilkov, “Survey of maneuvering target tracking. Part I: Dynamic models, ”IEEE Transactions on Aerospace and Electronic Systems, 39(4), 2003.
[7] S.J. Julier, and J.K. Uhlmann, “A New Extension of the Kalman Filter to Nonlinear Systems,” Signal Processing, Sensor Fusion, and Target Recognition VI, vol. 3068, Proc. SPIE, pp. 182–193, 1997
[8] A.H. Jazwinski, “Stochastic Processes and Filtering Theory,” Chapter 8, pp. 272–281, Academic, New York, 1970
[9] F. Gustafsson, “Statistical Sensor Fusion,” Studentlitteratur, 2018


