原文:https://arxiv.org/abs/1901.00596
网友对本文的评价
本文第一版的阅读笔记,知乎获赞2000+
我阅读是的是原文的第四版,论文各版本内容差异较大 [v1] Thu, 3 Jan 2019 03:20:55 UTC (3,958 KB)
[v2] Sun, 10 Mar 2019 03:15:39 UTC (1,992 KB)
[v3] Thu, 8 Aug 2019 05:13:16 UTC (5,849 KB)
[v4] Wed, 4 Dec 2019 01:43:00 UTC (2,712 KB)
Abstract
近年来,深度学习已经彻底改变了许多机器学习任务,从图像分类和视频处理到语音识别和自然语言理解。
在越来越多的应用中,数据是从非欧几里德空间中生成的,并且被表示为对象之间具有复杂关系和相互依赖性的图。图数据的复杂性给现有的机器学习算法带来了巨大的挑战。
最近,许多关于扩展图数据的深度学习方法的研究已经出现。在这篇综述中,我们提供了图神经网络在数据挖掘和机器学习领域的全面概述。我们提出了一种新的分类法,将最先进的图神经网络分为四类,即递归图神经网络、卷积图神经网络、图自动编码器和时空图神经网络。我们进一步讨论了图神经网络在各个领域的应用,并总结了图神经网络的开源代码、基准数据集和模型评估。最后,我们提出了这一快速发展领域的潜在研究方向。
1 Introduce
虽然深度学习可以有效地捕捉欧几里德数据(图片、文本和视频)的隐藏模式,但以图形式(非欧几里德空间)表示数据的应用越来越多。例如,在电子商务中,基于图的学习系统可以利用用户和产品之间的交互来做出高度准确的推荐。在化学中,分子被建模为图,它们的生物活性需要被识别以用于药物研究。在引文网络中,论文通过引文相互联系,它们需要被分成不同的组。
图数据的复杂性给现有的机器学习算法带来了巨大的挑战。由于图可以是不规则的,图可以具有可变大小的无序节点,并且来自图的节点可以具有不同数量的邻居,导致一些重要的操作(例如,卷积)在图像中易于计算,但是难以应用于图。此外,现有机器学习算法的一个核心假设是实例相互独立。这种假设不再适用于图数据,因为每个实例(节点)都通过各种类型的链接(如引用、友谊和交互)与其他实例相关联。
最近,人们对扩展图数据的深度学习方法越来越感兴趣。为了处理复杂的图数据,在CNNs、RNNs和自动编码器的推动下,图领域的新定义和新概念在过去几年中迅速发展。例如,图卷积可以由2D卷积推广而来。如图1所示,一幅图像可以被认为是一种特殊的图,其中像素由相邻的像素连接。类似于2D卷积,可以通过获取节点邻域信息的加权平均值来执行图卷积。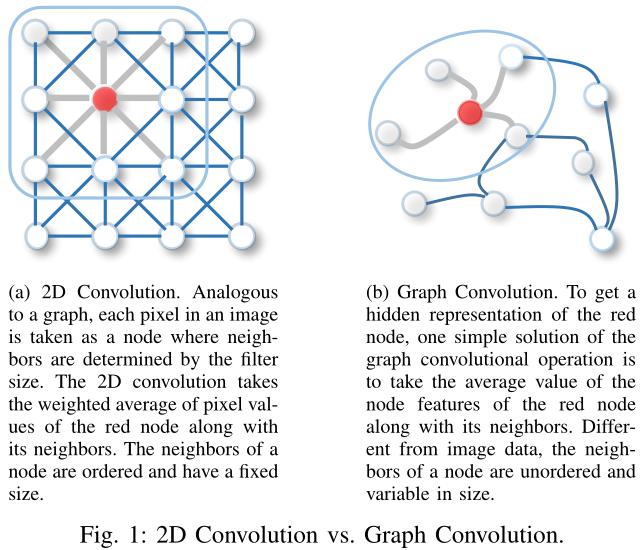
关于graph neural networks(GNNs)的现有综述数量有限。现有的综述只包括一些GNNs,并调查了数量有限的工作,从而错过了GNNs的最新发展。
我们的综述为想进入这个快速发展的领域的感兴趣的研究人员和想比较GNN模型的专家提供了一个关于GNNs的全面概述。为了涵盖更广泛的方法,该调查将GNNs视为图数据的所有深度学习方法。
本文的贡献
- 新的分类方法
我们提出了一种新的图神经网络分类法。图神经网络分为四类:递归图神经网络、卷积图神经网络、图自动编码器和时空图神经网络。
- 全面概述
我们为图数据提供了最全面的现代深度学习技术概述。对于每种类型的图神经网络,我们提供了代表性模型的详细描述,进行了必要的比较,并总结了相应的算法。
- 丰富的资源
我们收集了大量关于图神经网络的资源,包括最先进的模型、基准数据集、开源代码和实际应用。本调查可作为实践指南,帮助理解、使用和开发不同的深度学习方法用于各种实际应用。
本文的结构
本文的后续内容组织如下
- 第二节列出了常用的符号,并定义了图相关的概念。
- 第三节阐明了图神经网络的分类。
- 第四至第七节概述了图神经网络模型。
- 第八节介绍了跨不同领域的应用集合。
- 第九节讨论了当前的挑战,并提出了未来的方向。
- 第十节对论文进行了总结。
2 Definition
在本文中,我们使用粗体大写字符表示矩阵,粗体小写字符表示向量。除非特别说明,本文中使用的符号在表1中说明。
现在我们定义理解这篇文章所需的最小定义集:
- 定义1(图)
图表示为表示一个节点;
表示一条从
指向
的边
节点的邻居定义为
图的邻接矩阵定义为,其中值为1表示两个节点之间有边,为0则表示两个节点之间没有边
节点的特征矩阵定义为
边的特征矩阵定义为
- 定义2(时空图)
时空图的节点特征随时间动态变化
时空图定义为,其中
3 Categorization And Frameworks
3.1 Taxonomy of Graph Neural Networks (GNNs)
在这一节中,我们给出了图神经网络的分类,如下表所示:我们将图形神经网络分为递归图神经网络(Recurrent Graph Neural Network)、卷积图神经网络(Convolutional Graph Neural Networks)、图自动编码器(Graph Autoencoders)和时空图神经网络(Spatial-temporal Graph Neural Networks)
| Category | Sub Category | Publications |
|---|---|---|
| Recurrent Graph Neural Networks (RecGNNs) | The graph neural network model | |
| Graph echo state networks | ||
| Gated graph sequence neural networks | ||
| Learning steady-states of iterative algorithms over graphs | ||
| Convolutional Graph Neural Networks (ConvGNNs) | Spectral methods | Spectral networksand locally connected networks on graphs |
| Deep convolutional networks ongraph-structured data | ||
| Convolutional neural networks on graphs with fast localized spectral filtering | ||
| Semi-supervised classification with graph convolutional networks | ||
| Cayleynets:Graph convolutional neural networks with complex rational spectral filters | ||
| Adaptive graph convolutionalneural networks | ||
| Dual graph convolutional networks for graph-based semi-supervised classification | ||
| Spatial methods | Neural network for graphs: A contextual constructive approach | |
| Diffusion-convolutional neural networks | ||
| Learning convolutional neural networks for graphs | ||
| Neural message passing for quantum chemistry | ||
| Inductive representation learning on large graphs | ||
| Graph attention networks | ||
| Geometric deep learning on graphs and manifolds using mixture model cnns | ||
| Large-scale learnable graph convolutional networks | ||
| On filter size in graph convolutional networks | ||
| Contextual graph markov model:A deep and generative approach to graph processing | ||
| Gaan: Gated attention networks for learning on large and spatio temporal graphs | ||
| Fastgcn: fast learning with graph convolutional networks via importance sampling | ||
| Stochastic training of graph convolutional networks with variance reduction | ||
| Adaptive sampling towards fast graph representation learning | ||
| An end-to-end deeplearning architecture for graph classification | ||
| Deeper insights into graph convolutional networks for semi-supervised learning | ||
| Hierarchical graph representation learning with differentiable pooling | ||
| Geniepath: Graph neural networks with adaptive receptive paths | ||
| Deep graph infomax | ||
| How powerful are graph neural networks | ||
| Cluster-gcn: An efficient algorithm for training deep and large graph convolutional networks | ||
| Graph Autoencoders (GAEs) | Network Embedding | Deep neural networks for learning graph representations |
| Structural deep network embedding | ||
| Variational graph auto-encoders | ||
| Adversarially regularized graph autoencoder for graph embedding | ||
| Deep recursive network embedding with regular equivalence | ||
| Learning deep network representations with adversarially regularized autoencoders | ||
| Graph Generation | Learning deep generative models of graphs | |
| Graphrnn: A deep generative model for graphs | ||
| Graphvae: Towards generation ofsmall graphs using variational autoencoders | ||
| Constrained generation of semanticallyvalid graphs via regularizing variational autoencoders | ||
| MolGAN: An implicit generative modelfor small molecular graphs | ||
| Netgan: Generating graphs via random walks | ||
| Spatial-temporal Graph Neural Networks (STGNNs) | Structured sequence modeling with graph convolutional recurrent networks | |
| Diffusion convolutional recurrent neural network: Data-driven traffic forecasting | ||
| Structural-rnn: Deep learning on spatio-temporal graphs | ||
| Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting | ||
| Spatial temporal graph convolutional networks for skeleton-based action recognition | ||
| Graph wavenet fordeep spatial-temporal graph modeling | ||
| Attention based spatial-temporal graph convolutional networks for traffic flow forecasting |
图2给出了各种模型架构的例子: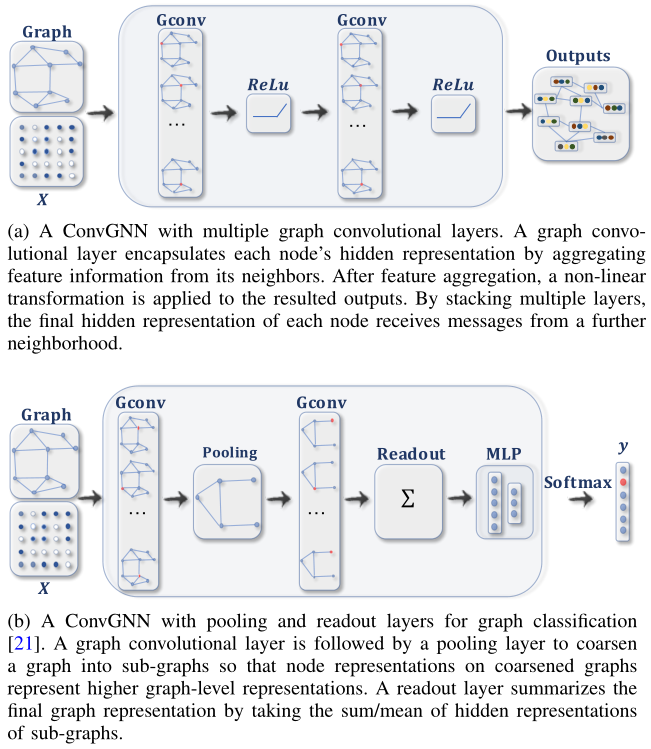


Recurrent graph neural networks (RecGNNs)
递归图神经网络可以说是图神经网络的先驱,旨在学习具有递归神经结构的节点表示。
RecGNNs假设图中的一个节点不断地与其邻居交换信息/消息,直到达到稳定的平衡。
RecGNNs在概念上很重要,并启发了后来对卷积图神经网络的研究。特别地,消息传递的思想被基于空间的卷积图神经网络继承。
Convolutional graph neural networks (ConvGNNs)
卷积图神经网络将卷积运算从网格数据推广到图数据。主要思想是通过聚集节点自身的特征和邻居的特征
(
)来生成节点
的表示。与RecGNNs不同的是,ConvGNNs堆叠多个图卷积层来提取高级节点表示。在建立许多其他复杂的GNN模型中,ConvGNNs起着核心作用。图2a展示了节点分类的ConvGNN,图2b展示了一个用于图分类的ConvGNN。
Graph autoencoders (GAEs)
图自动编码器是无监督学习框架,它将节点/图编码到潜在向量空间中,并从编码信息中重构图数据。GAEs用于学习网络嵌入和图生成分布。对于网络嵌入,GAEs通过重构图的结构信息(如图的邻接矩阵等)来学习潜在的节点表示。对于图生成,一些方法逐步生成图的节点和边,而另外一些方法一次输出整个图。图2c展示了用于网络嵌入的GAE。
Spatial-temporal graph neural networks (STGNNs)
时空图神经网络旨在从时空图中学习隐藏模式,这在各种应用中变得越来越重要,例如交通速度预测、驾驶行为预测和人类行为识别。STGNNs的核心思想是同时考虑空间相关性和时间相关性。当前的许多方法将图卷积用于捕捉空间相关性,而将CNNs或RNNs用于建模时间相关性。图2d展示出了用于时空图预测的STGNN。
3.2 Frameworks
不同级别的图分析任务
有了图结构和节点内容信息作为输入,GNNs的输出可以通过以下机制之一来专注于不同的图分析任务:
- Node-level
节点级输出与节点回归和节点分类任务相关。RecGNNs和ConvGNNs可以通过 information propagation/ graph convolution提取节点的高级表示。使用多感知机或softmax层作为输出层,GNNs能够以端到端的方式执行节点级任务。
- Edge-level
边级输出涉及边分类和链路预测任务。以两个节点的GNNs隐藏层输出作为输入,可以利用similarity function或neural network来预测边的标签或连接强度(边的权值?)。
- Graph-level
图级输出与图分类任务相关。为了在图级别上获得“紧凑”的表示,GNNs通常与pooling和Readout操作相结合。关于pooling和Readout的详细信息将在后面讨论
训练框架
很多GNNs(如ConvGNNs)可以在端到端的学习框架内以(半)监督或纯粹无监督的方式进行训练,这取决于手头的学习任务和标签信息。
- 用于节点级分类的半监督学习(Semi-supervised learning for node-level classification)
给定单个网络,其中部分节点有标签,而其他节点没有标签,ConvGNNs可以学习一个健壮的模型,该模型可以有效地识别未标记节点的类别标签(如Semi-supervised classification with graphconvolutional networks)。为此,可以通过堆叠两个图卷积层,然后再堆叠一个softmax层来进行多分类,从而构建端到端框架。
- 用于图级分类的监督学习(Supervised learning for graph-level classification)
图级分类旨在预测整个图的类别标签(如An end-to-end deeplearning architecture for graph classification、Hierarchical graph representation learning with differentiable pooling、Joint structure feature exploration and regularization for multi-task graph classification、Task sensitive feature exploration and learning for multitask graph classification)。该任务的端到端学习可以通过图卷积层、图池化层和/或读出层的组合来实现。虽然图卷积层负责提取高级节点表示,但graph pooling层起到下采样的作用,每次都会将每个图粗化为一个子结构。Readout层将每个图的节点表示折叠成图表示。通过将MPL和softmax层应用于图表示,我们可以构建一个端到端的图分类框架。图2b给出了一个例子。
- 用于图嵌入的无监督学习(Unsupervised learning for graph embedding)
当图中没有可用的类标签时,我们可以在端到端框架中以纯无监督的方式学习图嵌入。这些算法以两种方式利用边级信息。一种简单的方法是采用自动编码器框架,其中编码器采用图卷积层将图嵌入到潜在表示中,在此基础上解码器用于重建图结构。另一种流行的方法是利用负采样(negative sampling)方法,该方法将一部分节点对采样为负对,而图中具有链接的现有节点对是正对。然后应用logistic regression层来区分正负对。
在表三中,我们总结了有代表性的RecGNNs和ConvGNNs的主要特征。输入源、pooling层、Readout层和时间复杂度在各种模型之间进行比较。具体来说,我们只比较每个模型中message passing/graph convolution operation的时间复杂度。表三缺少几种方法的时间复杂度。这些方法要么在论文中缺乏时间复杂度分析,要么报告其整体模型或算法的时间复杂度。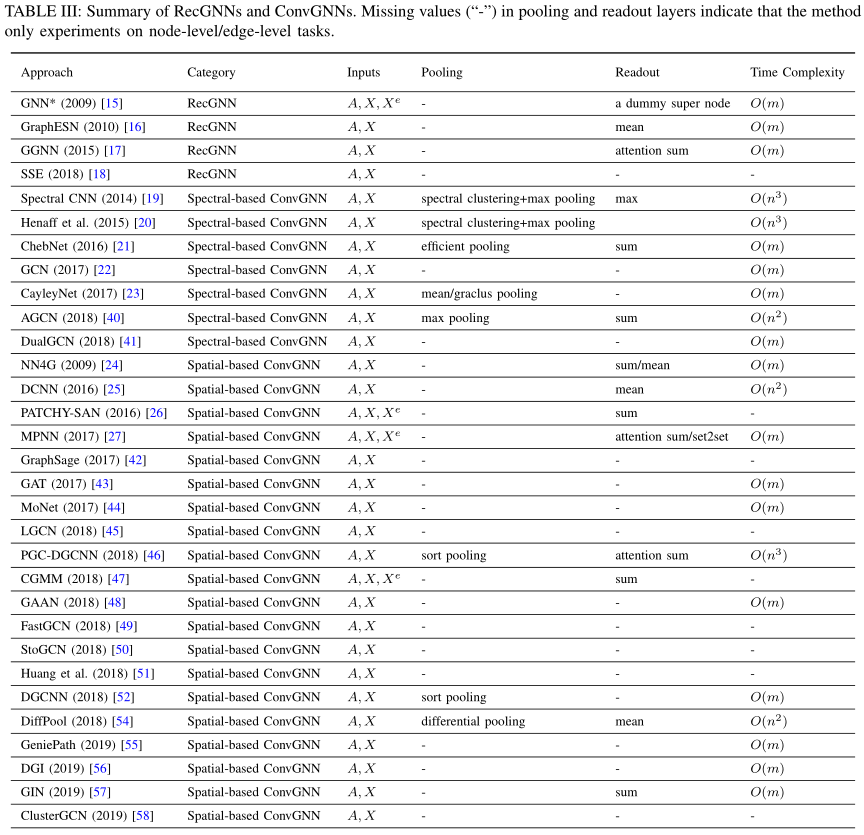
4 Recurrent Graph Neural Networks
RecGNNs大多是GNNs的前驱作品。它们在图中的节点上反复应用相同的参数集,以提取高级节点表示。受计算能力的限制,早期的研究主要集中在有向无环图。
5 Convolutional Graph Neural Networks
卷积图神经网络与递归图神经网络密切相关。ConvGNNs不是用收缩约束来迭代节点状态,而是使用固定数量的层,每层具有不同的权重来解决结构上的循环相互依赖(即RecGNNs使用同一层迭代特征,而ConvGNNs则使用不同的、固定数量的卷积层来更新特征)。这一关键区别如图3所示。由于图卷积与其他神经网络相结合的效率更高、更方便,近年来ConvGNNs得到了迅速发展。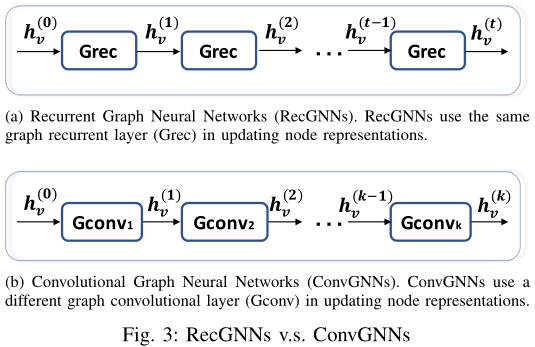
ConvGNNs分为两类,基于频谱的(spectral-based)和基于空间的(spatial-based)。
- 基于频谱的方法通过从图信号处理的角度引入滤波器来定义图卷积,其中图卷积运算被解释为从图信号中去除噪声。
- 基于空间的方法继承了RecGNNs的思想,通过信息传播(information propagation)来定义图卷积。自从GCN 弥合了基于频谱的方法和基于空间的方法之间的差距以来,基于空间的方法由于其效率、灵活性和通用性而在最近得到了快速发展。
5.1 Spectral-based ConvGNNs
5.2 Spatial-based ConvGNNs
5.3 Graph Pooling Modules
GNN生成节点特征后,我们可以将它们用于最终任务。但是直接使用所有这些特征在计算上具有挑战性,因此,需要一种下采样策略。根据目标及其在网络中扮演的角色,该策略有两个不同的名称:
- pooling操作旨在通过对节点进行下采样以生成更小的表示来减小参数的大小,从而避免过拟合、置换不变性(permutation invariance)和计算复杂性问题;
- Readout操作主要用于基于节点表示生成图表示。
上述两个操作的机制很相似。在本章中,我们使用pooling来指代应用于GNNs的各种下采样策略。
在一些早期的工作中,图粗化算法(graph coarsening algorithms)使用特征分解(eigen-decomposition)根据图的拓扑结构来粗化图。然而,这些方法受到时间复杂性问题的困扰。Graclus算法(Weighted graph cuts withouteigenvectors a multilevel approach, 2007)是一种代替特征分解的方法,用于计算原始图的聚类版本。最近的一些工作(Cayleynets: Graph convolutional neural networks with complex rational spectral filters, 2017)使用Graclus算法作为一个pooling操作来粗化图。
现在,mean/max/sum pooling是实现下采样的最原始的也是最有效的方法,因为计算mean/max/sum值的速度很快:
其中K是最后一个图卷积层的索引。
Deep convolutional networks ongraph-structured data, 2015表明,在网络开始时执行简单的max/mean pooling对于降低图域的维数和降低图傅立叶变换操作的成本特别重要。
一些工作(Gated graph sequence neural networks, ICLR 2015、Neural message passing for quantum chemistry, ICML 2017、On filter size in graph convolutional networks, IEEE 2018)使用注意力机制来增强mean/sum pooling。
即使有注意机制,约简操作(如sum pooling)也不能令人满意,因为它使嵌入变得低效,因为不管图大小如何,都会生成固定大小的嵌入。Order matters: Sequence tosequence for sets, ICLR 2016提出了Set2Set方法来生成一个随输入大小而增加的内存。然后,该论文还实现了一种LSTM算法,该算法旨在约简操作实施前,将依赖于顺序的信息集成到内存嵌入中,否则约简操作可能会破坏该信息。
Convolutionalneural networks on graphs with fast localized spectral filtering, NIPS 2016通过以有意义的方式重新排列图的节点,以另一种方式解决了这个问题。该论文在其方法ChebNet中设计了一个有效的pooling策略。输入图首先通过Graclus算法粗化为多个级别。粗化后,输入图的节点及其粗化版本被重新排列成平衡二叉树。自下而上聚合平衡二叉树会将相似的节点排列在一起。pooling这样一个重新排列的信号比pooling原始信号要有效的多。
An end-to-end deeplearning architecture for graph classification, AAAI 2018提出了DGCNN,其具有相似的pooling策略,称为SortPooling,其将节点重新排列成有意义的顺序来执行pooling。与ChebNet不同,DGCNN根据节点在图中的结构角色(structural roles)来对节点进行排序。来自空间图卷积的图的无序节点特征被视为连续WL颜色(A reduction of a graph to a canon-ical form and an algebra arising during this reduction, 1968),然后它们被用于对节点进行排序。除了对节点特征进行排序,该论文还通过截断/扩展节点特征矩阵将图大小统一为q。如果n>q,则删除最后n-q行,否则添加q-n个零行。
上述pooling方法主要考虑图的特征,而忽略了图的结构信息。最近,Hierarchical graph representation learning with differentiable pooling, NIPS 2018提出了一种可微pooling(DiffPool),它可以生成图的分层表示(hierarchical representations)。与所有之前的粗化方法相比,DiffPool不是简单地对图中的节点进行聚类,而是在k层学习聚类分配矩阵(cluster assignment matrix)S,具体来说是,其中
是第k层的节点数量。矩阵
中的概率值是基于节点特征和图的拓扑结构生成的,如下公式
其核心思想是学习全面的节点分配,其中考虑了图的拓扑和特征信息,因此上述等式可以用任何标准的ConvGNNs实现。然而,DiffPool的缺点是,它在合并后生成密集的图,此后计算复杂度变为。
最近,Self-attention graph pooling, ICML 2019提出了SAGPool方法,该方法考虑了节点特征和图拓扑,并以self-attention的方式学习pooling。
总的来说,pooling是减少图大小的基本操作。如何提高pooling的有效性和计算复杂度是一个有待研究的问题。
6 Graph Autoencoders
7 Spatial-Temporal Graph Neural Networks
8 Applications
由于图结构的数据无处不在,所以GNNs有着广泛的应用。在本节中,我们分别总结了图数据集、评估方法、开源实现和各领域的实际应用。
8.1 Graph Data Sets
我们主要将数据集分为四组,即引用网络(citation networks)、生化图(biochemical graphs)、社交网络(social networks)和其他。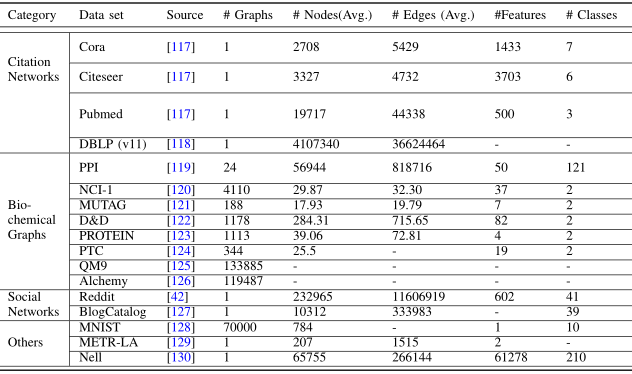
Biochemical Graphs
化学分子和化合物可以用原子为节点、化学键为边的化学图来表示。这类图通常用于评估图分类性能。
NCI-1和NCI-9数据集分别包含4110和4127种化合物,每种化合物的类别为是否具有阻碍人类癌细胞株生长的活性。
MUTAG数据集包含188种硝基化合物,根据它们是芳香族还是杂芳香族进行标记。
D&D和PROTEIN数据集将蛋白质表示为图,标记它们是酶还是非酶。
PTC数据集由344种化合物组成,标记为它们对雄性和雌性大鼠是否致癌。
QM9数据集记录了133885个分子的13种物理性质,这些分子包含多达9个重原子。
Alchemy数据集记录了119487个分子的12种量子力学性质,这些分子包含多达14个重原子。
另一个重要的数据集是Protein-Protein Interaction network,PPI(蛋白质相互作用网络)。它包含24个生物图,节点由蛋白质表示,边由蛋白质之间的相互作用表示。在PPI中,每个图与一个人体组织相关联。每个节点都标有其生物状态。
8.2 Evaluation & Open-source Implementations
节点分类和图分类是评估RecGNNs和ConvGNNs性能的常见任务。
Node Classification
Graph Classification
在图分类中,研究人员通常采用10倍交叉验证(10-fold cross validation)进行模型评估。
10-fold cross-validation(10 fold CV),用来测试算法准确性,是常用的测试方法。该方法需要将数据集分成10份,轮流将其中9份作为训练数据,1份作为测试数据,进行试验。每次试验都会得出相应的正确率(或差错率)。10次结果的正确率(或差错率)的平均值作为对算法精度的估计。
最近,A fair comparison of graph neural networks for graph classification, ICLR 2020指出,图分类的实验设置是模糊的,并且在不同的作品之间不统一。该论文提出了模型选择和模型评估中正确使用数据分割的问题,并且在标准化和统一化的评估框架中评估了各种GNNs。如果需要获得图分析的GNNs方法的详细和严格的比较,请参考本篇文章。


