李航统计学习方法第二章学习笔记 by 沉默的山岭
Minsky与Papert指出,感知机因为是线性模型,所以不能表示复杂的函数,如异或(XOR)。验证感知机为什么不能表示异或。
异或的真值表如下:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
将上述数据在坐标上标示出来: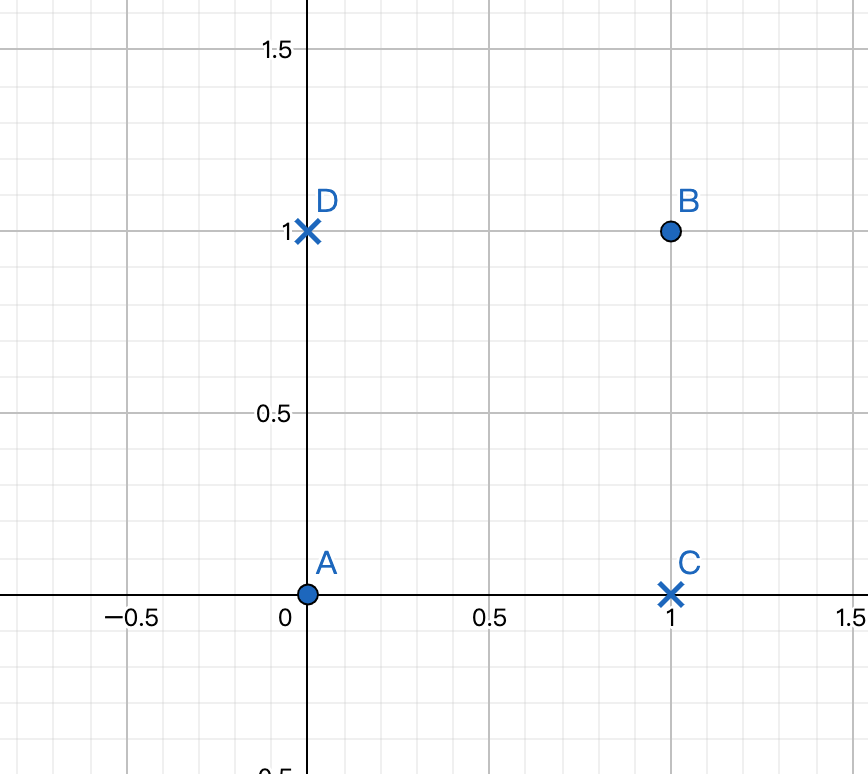
直观的可以看到,这四个点线性不可分。因此感知机不能表达出异或函数。
已知训练数据集D,其正实例点是x1=(4,4)T,x2=(5,3)T,负实例点是x3=(2,1)T:
(0) 模仿例题2.1,构建从训练数据集求解感知机模型的例子。
A: 感知机原始算法形式:
初始值设为,迭代过程如下表所示:
| 迭代次数 | 误分类点 | w | b | wx+b |
|---|---|---|---|---|
| 0 | 判断方法:计算wx+b,看结果和正负实例是否一致 | 初始化:(0,0)T |
初始化:0 |
0 |
| 1 | x3 | (-2,-1)T | -1 | |
| 2 | x1 | (2,3)T | 0 | |
| 3 | x3 | (0,2)T | -1 | |
| 4 | x3 | (-2,1)T | -2 | |
| 5 | x1 | (2,5)T | -1 | |
| 6 | x3 | (0,4)T | -2 | |
| 7 | x3 | (-2,3)T | -3 | |
| 8 | x2 | (3,6)T | -2 |
8轮迭代后得到了一个分类器:, 能够正确分类三个样本。如下图所示。
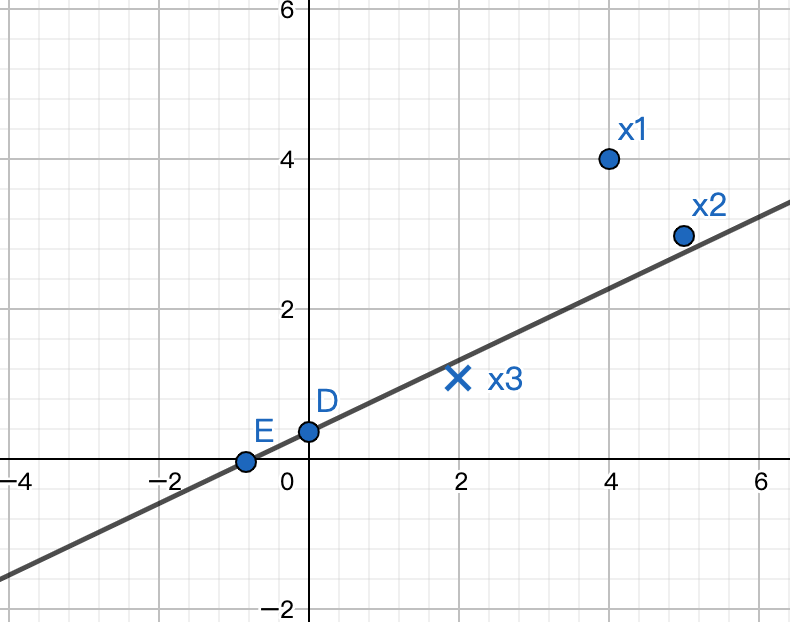
可以“感觉”得到,上述的分类器可能并不是最优的。因为它太贴近x3和x2了。支持向量机算法能够选择出更“健壮”的分类器,详见《统计学习方法》第七章。
B: 感知机对偶算法形式:利用对偶形式求感知机模型,同例2.2
判断误分类点的条件仍然是。带入w后:
在机器学习中会经常看到,是训练集自己的内积,叫做Gram矩阵。因为Gram矩阵每次迭代中是不变的,因此可以先求出来。
各个参数初始化值为1,学习率, 具体迭代过程如下表:
| 迭代次数 | 误分类点 | b | wx+b | |||
|---|---|---|---|---|---|---|
| —- | 判断方法: 则为误分类点 |
初始化:0 迭代: (只更新误分类点对应的i |
初始化:0 | w: |
||
| 0 | 1 | 0 (不变) | 0 (不变) | 1 | 暂不计算 | |
| 1 | 1(不变) | 0 (不变) | 1 | 0 | 暂不计算 | |
| 2 | 1(不变) | 0 (不变) | 2 | -1 | 暂不计算 | |
| 3 | 1(不变) | 0 (不变) | 3 | -2 | 暂不计算 | |
| 4 | 2 | 0 (不变) | 3 (不变) | -1 | 暂不计算 | |
| 5 | 2(不变) | 0 (不变) | 4 | -2 | 暂不计算 | |
| 6 | 2(不变) | 0 (不变) | 5 | -3 | 暂不计算 | |
| 7 | 2(不变) | 1 | 5 (不变) | -2 | 暂不计算 | |
| 8 | 2(不变) | 1 (不变) | 6 | -3 | 暂不计算 | |
| 9 | 2(不变) | 1 (不变) | 7 | -4 | 暂不计算 | |
| 10 | DONE | 2 | 1 | 7 | -4 |
该分类器如下图所示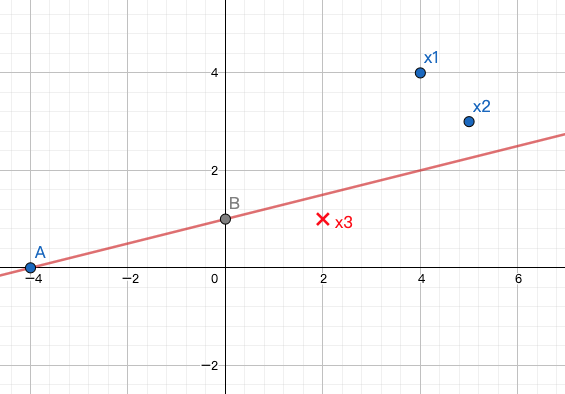
(1) 用python 自编程实现感知机模型,对训练数据集进行分类,并对比误分类点选择次序不同对最终结果的影响。
import numpy as npdata = np.array([[4, 4], [5, 3], [2, 1]])label = np.array([1, 1, -1])w = np.array([0, 0])b = 0distance = label * np.dot(w, data.T) + berror_data = np.where(distance <= 0)print(len(error_data))lmt = 100loop_cnt = 0eta = 1# print(error_data[0][0])# print(label[error_data[0][0]] * data[error_data[0][0]])# print(eta * label[error_data[0][0]])while len(error_data[0]) > 0 and loop_cnt < lmt:loop_cnt = loop_cnt + 1error_to_fix = error_data[0][len(error_data[0])-1]#error_to_fix = error_data[0][0]print("error sample index is ", error_to_fix)print("error sample is ", data[error_to_fix])w = w + eta * label[error_to_fix] * data[error_to_fix]b = b + eta * label[error_to_fix]print("w is ", w)print("b is ", b)distance = label * (np.dot(w, data.T) + b)print("distance is ", distance)error_data = np.where(distance <= 0)print("error data is ", error_data)print("error count is ", len(error_data[0]))print("loop:", str(loop_cnt), " error count", str(len(error_data)))print("result model is, w:", w, " b: ", b)
(2)试调用sklearn.linear_model 的Perceptron模块,对训练数据集进行分类,并对比不同学习率h对模型学习速度及结果的影响。
import numpy as npfrom sklearn.linear_model import Perceptrondata = np.array([[3, 3], [4, 3], [1, 1]])label = np.array([1, 1, -1])clf = Perceptron()clf.fit(data, label)s = clf.score(data, label)print(s)print("w ", clf.coef_, " b: ", clf.intercept_, "iter no:", clf.n_iter_)
思考感知机模型假设空间是什么?模型复杂度体现在哪里?
感知机模型的假设空间是定义在特征空间中的所有超平面。模型的复杂度 = (特征的维度数+1),是所有参数的个数。
证明以下定理:样本集线性可分的充要条件是正实例点集所构成的凸壳与负实例点集所构成的凸壳互不相交。
维基百科的凸壳定义如下:
In mathematics, the convex hull or convex envelope or convex closure of a set X _of points in the Euclidean plane or in a Euclidean space(or, more generally, in an affine space over the reals) is the smallest convex set that contains _X. For instance, when X _is a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around _X.
在数学中,一组点集X的凸包或凸包络或凸闭合定义为在欧几里得平面或在欧氏空间(或者,更一般地,在一个仿射空间在实数)是最小的包含X的凸集。例如,当X是平面的有界子集时,凸包可以被视为由围绕X拉伸的橡皮筋包围的形状。
根据这个定义,直观层面比较容易理解,两个凸壳不相交,说明两个区域之间没有overlap,那么总能找到一个超平面把两者划分开来。反之亦然。数学上的推导要更严格。具体可以参照这里:凸壳与线性可分

