引子
大西洋彼岸的飓风可能是由于亚马逊丛林里的蝴蝶扇动了翅膀。现实世界里的事件关系如此错综复杂，扑朔迷离。如果我们要为这个复杂迷离的世界建模描述，甚至卜算未来，是不是就无能为力了呢？马克思主义的方法论指导我们解决问题要抓住主要矛盾，那么如何才能舍弃枝叶末节，能够大道至简？
假设说有一个简化了的世界W，有N个维度就能够充分描述这个世界。每个维度都能以不同的概率取到M个的状态。那么，用概率理论来建模这个世界，我们需要的参数（概率的个数）将是 M-1 之多（因为概率总和为 1 ，因此参数个数可以减掉 1）。在计算机的世界里，指数级的复杂度是我们要尽量避免的。也许在通用的量子计算机诞生前，规模稍大的指数级的问题基本无法求解。因此，必须做出一些不同层次的简化假设来削减系统的参数个数。基于不同层面和不同程度的简化假设，诞生了不同的概率模型。参数和参数之间的相互依赖用箭头或者连线图示出来，就构成了概率图。
概率图模型
在现实中概率模型常见的任务是：构建一个简化世界的概率模型，即所有变量的联合概率分布。估算参数。然后计算部分变量的边缘概率，或者条件概率，来估算某一类事件或者状态发生的概率。
概率图模型（Probabilistic Graphical Model， PGM），简称图模型（Graphical Model，GM），是指一种用图结构来描述多元随机变量之间条件独立性的概率模型，从而给研究高维空间的概率模型带来了很大的便捷性。
条件独立性
之所以在这里强调条件独立性，是因为在概率模型中，只有具备条件独立性，才能够降低参数个数。
如下图所示。假设一个简化世界可以用四个随机二值变量描述。这四个随机变量的联合分布的参数个数是
。假设
只依赖于
, 
只依赖于, 
只依赖于
和, 那么，根据概率的链式法则，联合分布可以表示为：
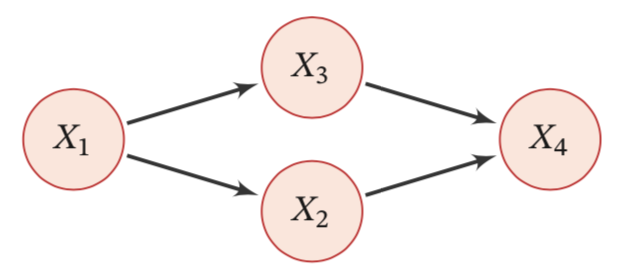
上面的图来自于参考 1
这种情况下，需要多少的参数表示呢？
| 式子 | 参数个数 |
|---|---|
| 1 （e.g 2-1)，有两个取值，总和为 1 ，所以只需要一个参数即可。 | |
| 2 (e.g. 2*(2-1)) 有两个取值。每种取值下，都有一个条件概率，因此每种取值需要一个参数，两种取值两个参数。 | |
| 2 (e.g. 2*(2-1)) 同上 | |
| 4 (e.g. 4*(2-1)) 计算方法同上 | |
| 总计 | 9 |
参数个数明显变少了。如果是一个更复杂参数更多的系统，这种因为条件独立性而引起的“瘦身”会更明显。
上面的是以有向图作为例子的。无向图也会通过独立性假设（即马尔可夫性）来降低模型的复杂度。道理都是相通的。
概率图模型应用模式
概率图模型应用的模式一般分为三个步骤：第一，确定概率图的结构（即下图所说的表示），即定义一个网络结构来表征感兴趣的世界（或者可以称之为领域）。第二，确定概率图的参数，即各个概率、条件概率的取值（即下图所说的学习）。第三，利用算法求解边缘概率和条件概率来回答各种感兴趣的问题（即下图所说的推断）。本文初步总结了概率图的结构。学习和推断最好是结合具体的模型来阐述会更合理，因此暂时不包含在本文中。
下面的图来自于参考 1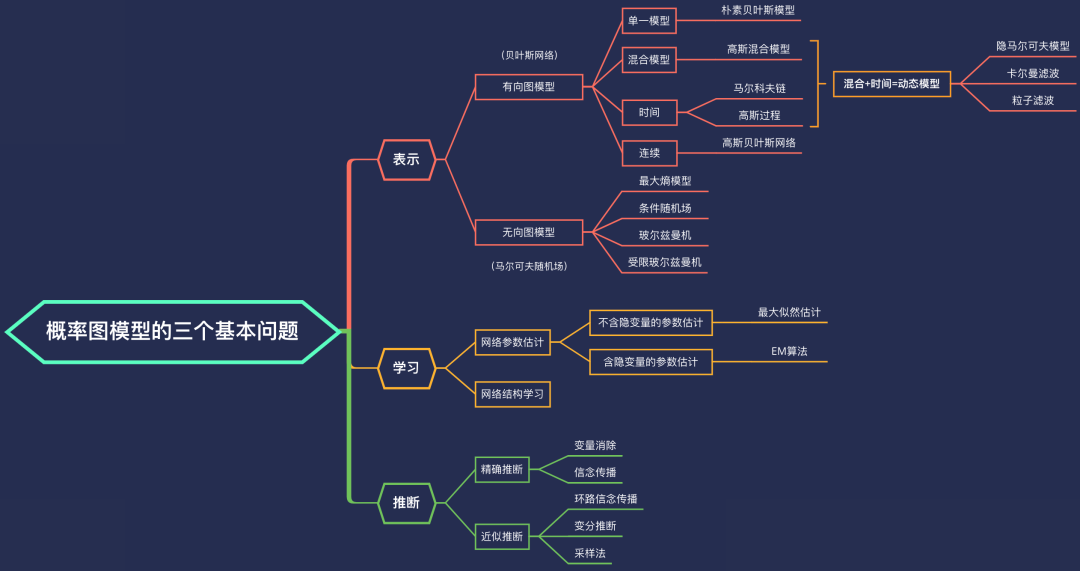 
概率图的网络结构
针对一个简化世界，我们要选择的建模方式，既取决于该世界本身的特质，也需要考虑我们建模后要完成的任务。对于概率图模型，一个重要的选择是我们要建模因果关系（因果，间接因果，共因，共果），还是相关关系。
贝叶斯网络
贝叶斯网络用来建模因果关系。我们看这样一个生活场景：
这里描述的就是四个事件之间存在的因果关系。这种网络结构被称为贝叶斯网络。它是一种有向图模型(DAG)。常见的贝叶斯网络的在上图中已经列出。部分模型会在后续笔记中详细阐述。
上述贝叶斯网络的联合概率可以表示为：
摘自参考1： 在贝叶斯网络中，变量间存在如下四种关系：
- 如果两个节点是直接连接的，它们肯定是非条件独立的，是直接因果关系。其中父节点是“因”，子节点是“果”。
- 间接因果关系（head-to-tail），即图（a）、图（b）：当
- 共因关系（tail-to-tail），即图（c）：当
。
- 共果关系（head-to-head），即图（d）：当
马尔科夫随机场/马尔科夫网络
马尔科夫网络用来建模相关关系。我们来看另外一个生活场景。对一个年级的中学生学习情况进行考察，发现数学成绩和英语成绩存在相关关系。英语成绩和音乐成绩存在相关关系。但给定英语成绩情况下，数学成绩和音乐成绩未发现相关关系。在图中，我们用无向边来代表相关关系。
这种网络结构我们就叫做马尔科夫随机场或马尔科夫网络。马尔科夫随机场中，一个节点的概率仅仅受其相邻节点的影响（这个说法数学意义上不够严格。严格的说法应该是局部马尔可夫性，全局马尔可夫性，以及成对马尔可夫性）。马尔科夫网络又叫概率无向图。
这里有一个最大团的概念。我们把马尔科夫随机场中，最大连通子图（就是子图中所有节点都是两两相连，且无法往这个团当中加入更多的节点）叫做最大团。比如上述的马尔科夫随机场中，数学成绩和英语成绩是一个最大团，而英语成绩和音乐成绩是另外一个最大团。
根据Hammersley-Clifford定理，马尔科夫随机场的联合概率分布可以表示为以规范化后的最大团的势函数的乘积。
即：
其中C为G中的最大团集合，
是定义在团
上的势能函数（Potential Function），
是配分函数（Partition Function），用来将乘积归一化为概率形式：
而势能函数一般选择严格为正的指数函数，即一般为：
。其中
为能量函数。
参考
概率图模型系列 (一) : 概率图模型简介
条件随机场(CRF)
如何用简单易懂的例子解释条件随机场（CRF）模型？它和HMM有什么区别？ - 知乎
若有收获，就点个赞吧
0 人点赞
