李航 统计学习方法 第七章学习笔记 by 沉默的山岭
因为支持向量机可以视作是感知机的进一步发展,所以提前把支持向量机的学习完成
概述
本章的内容非常多,所以需要先对内容的总体有个了解,不然扎到细节里就会迷失掉了。
支持向量机可以视作是感知机的进一步发展。在第二章中学习过的感知机只支持线性可分的数据集,学习得到的分离超平面是不唯一的,而且对于噪声数据很敏感,不够健壮。支持向量机能够解决感知机原来的局限性。
| 问题 | 解决方法 |
|---|---|
| 感知机能够学习出那么多的分离超平面,哪个是最好? | 学习出一个唯一且最优的分离超平面,作为预测的依据。-> 线性可分支持向量机/硬间隔支持向量机 |
| 感知机对于分离超平面附近噪声点很敏感,会导致不收敛。 | 找到一个能容忍少量噪声数据,而整体数据大致仍然线性可分的算法。-> 软间隔支持向量机 |
| 感知机只能支持线性数据,无法从线性不可分的数据中学习出模型。 | 利用核技巧学习出支持非线性可分数据集的模型。 |
针对不同的问题,支持向量机提供了不同的解决方法,这是理解掌握本章内容的一条线索。
另外一条重要的学习线索是拉格朗日函数,KKT条件等。这部分也是要理解的。
最后可能还需要关注下核函数,以及每个核函数较适用的场景。核方法、核技巧是具有普适性的方法,不光是非线性的支持向量机中使用。核函数和拉格朗日函数的部分参考各自单独的笔记。
硬间隔向量机
简介
对于线性可分的数据集,我们在感知机一章中已经得知,存在无穷个分离超平面能够将其分割开来,然后利用分离超平面对于新的样本进行预测。学习得到的分离超平面和初始值以及学习过程中误分类点的选择都有关系。那么,是否存在一种方法,能获得确定的和初始化值无关最优分离超平面呢?
这种方法就是支持向量机。对于线性可分的数据集,我们可以采用硬间隔向量机算法来找到最优分离超平面。简单来说,这种最优分离超平面的最优体现在分离超平面位于两类数据(正类和负类)的距离的最中间,因而尽可能地保持了和两类数据的最大距离。因此对于新样本的预测,可能预测结果更准确。
理解下面的内容需要先理解拉格朗日函数。
函数间隔与几何间隔
函数间隔。反映了任意一个点到
代表的超平面的距离。但是因为函数间隔在给定点和超平面后本身不唯一(缩放系数会导致函数间隔相应变化),并且无法比较同一个点到不同超平面的距离,如果对函数间隔利用范数进行规范化,那么就得到了几何间隔
。
同时,我们定义点集T和超平面之间的集合间隔为集合中所有点到超平面的几何间隔的最小值,即:
间隔最大化
为了确定出最优分离超平面,我们需要找到能分离正负样本集合,且和正负样本集合几何距离最大的那个超平面。这个问题可以表述为
带入函数间隔得到
因为函数间隔可以缩放而不影响超平面自身,为简便计算我们可以让函数间隔为1。同时最大化和最小化
等价,我们得到了一个凸二次规划问题如下:
解决这个问题就能得到最优超平面。
在训练数据集线性可分的情况下,离分离超平面最近的样本点满足如下条件:
这些实例被称为支持向量。支持向量是确定分离超平面的关键数据。可以说只有很少的“重要”样本确定出了支持向量机,因此相对而言,支持向量机只需要比较少的训练数据集就能学到效果还算不错的模型。补充说一句,在拉格朗日函数里,只有支持向量对应的互补松弛条件里的系数不为零。
对偶问题
对于上面的凸二次规划问题,其符合拉格朗日强对偶性的要求。其对偶问题是拉格朗日函数的极大极小问题:
其中为拉格朗日乘子向量。
步骤一 求解
对拉格朗日函数分别对w,b求偏导(注意不能对a求偏导,因为最小是针对w,b的,不是针对拉格朗日乘子的)。
因此有:
将上述求解结果回带入拉格朗日函数:
(a, y都是N维向量。w的维度和样本的维度一致。)
步骤二 求解 就等价于对
求极大,等于等下面的式子求极小:
所以最终优化函数转换为:
根据KKT条件求解上述最优化问题 (SMO算法,后面展开) — 求导
—求导
—互补松弛条件
— 求导得来
— 拉格朗日乘子要求
得到最优解记做 。
步骤三 求解分类模型
我们原始的问题是要得到最优模型对应的
。由步骤一中的等式可知:
由互补松弛条件可知,存在一个
的分量,使得下式成立:
然后我们就得到了分离超平面
分类决策函数
软间隔向量机
简介
硬间隔向量机并不是完美的。它仍然存在对于个别支持向量过于敏感,以及遇到噪声数据引起的极少数线性不可分数据就会失灵的问题。这时,我们可以引入软间隔最大化的方式来得到更健壮的分离超平面。
软间隔的意思是说,放弃要求对所有样本点函数间隔必须大于等于1的约束。但是对于不满足函数间隔大于等于的点,会增加上一个惩罚项。在此新的约束条件下,求解出一个分离超平面。
软间隔向量机有以下的特点
- 支持线性不可分数据(整体上仍然是线性近似可分,但有少部分点不可分)
- 分离超平面较少受到单个样本的影响,对错误标注数据容忍性更高
- 支持向量个数远多于硬间隔向量机。支持向量不一定都分布在函数间隔为1的间隔边界上。
- 软间隔向量机可能不唯一。
如下图: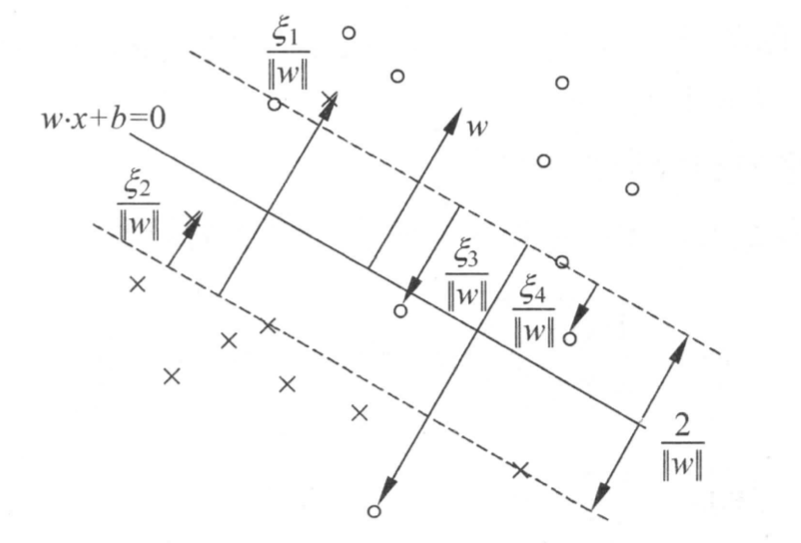
上图中,我们可以看到大部分支持向量分布在间隔边界分离超平面围成的中间区域。少部分支持向量可能会越过对方间隔边界,彻底被误分类。但所有的支持向量到它对应间隔边界的函数距离都。误分类的容忍程度可以通过调整惩罚力度来控制。如果惩罚力度为无穷大,那么软间隔向量机退化为硬间隔向量机。
原始形式与对偶形式
如上所述,软间隔支持向量机优化问题的原始形式如下:
对上述式子可以理解为一方面我们要使得间隔尽可能地大,同时要让误分类尽可能地小。C代表了对误分类以及不在间隔边界上点的惩罚力度。
显然上述优化问题仍然是一个带约束的凸函数优化。可以用拉格朗日对偶方法来解决。其对偶问题为:
推导过程和硬间隔向量机的推导过程一致,不再重复。
要得到最优模型对应的
:
存在一个
的分量,得到:
然后我们就得到了分离超平面
因为可能有多个点满足 ,所以计算得出的
可能不唯一。
分类决策函数
合页损失函数
对于软间隔支持向量机,其还可以被理解为最小化以下的目标函数:
第一项是经验损失,下标“+”表示函数为正时取得正值,为负时取零。第二项可以理解为L2范数,正则化项。
这个损失函数被称为合页损失函数 (hinge loss function)。它的特点是对于确信度较低的正确分类项也会产生损失。因此是比0-1损失更严格的损失函数。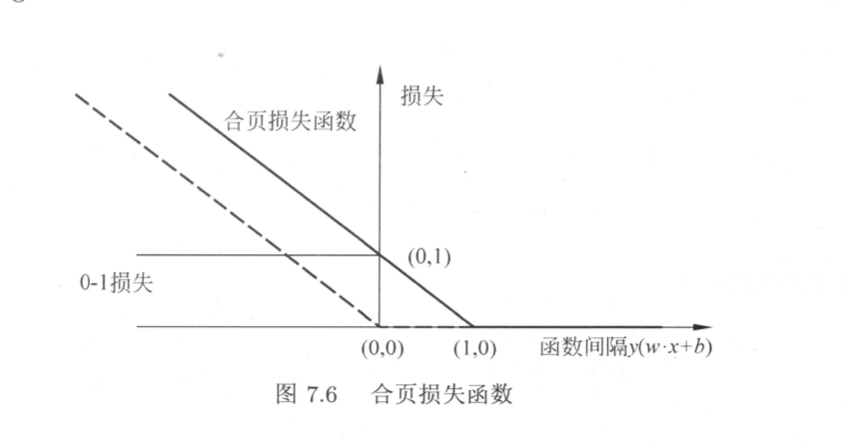
非线性支持向量机
通过使用核技巧,我们也能够处理非线性分类问题。关于核技巧的部分,可以参考核方法专题。
引入核技巧后,优化的问题就变为如下问题:
要得到最优模型对应的
:
存在一个
的分量,得到:
然后我们就得到了分离超平面
SMO算法
在上面几种支持向量机中,在得到对偶问题后如何用算法求解?课本里介绍了Platt提出的SMO算法。它的求解原理如下:
- 如果所有的
都满足KKT条件,那么
就是要找的解。
- 如果
中有分量不满足KKT条件,那么
- 选择出一个最不满足条件的
(即优先选择支持向量对应的
,即约束条件取值不为零的)。
- 因为整体有
的约束,所以还要找到一个
,使得对
的修改不违反这个约束。
- 在选定
后,假设其他分量都为常量,直接用解析方法求出两个变量的最优值。
- 选择出一个最不满足条件的
- 重复上述2直到完成。
上述算法中有两个比较关键的点,第一是如何选择,
书上提到了要违反KKT条件最严重的样本点。其实这个词很让人困扰。KKT条件要么违反,要么未违反,如果要度量违反的严重程度,那么就应该给出一个度量的方法。可惜这个度量方法并没有明确给出来,所以比较让人困惑。我这里的理解是这样的。首先应该选择支持向量对应的,即
。看这个点是否违反了KKT。对于违反的点,计算它和当前分离超平面的距离。距离越远的我们就认为违反越严重。
选择了第一个点后,选择另一个距离与它最远点,来进行调整。优先选择对侧支撑向量里的点。
再来看第二点:两个变量的二次规划求解。
两个变量在有约束条件下,其实等同于一个变量。而单变量的二次规划是有解析解的(抛物线),SMO算法的长处就在于其每一个子步骤是有解析解的,因此迭代收敛速度会很快。
整个SMO算法推导过程涉及的数据知识并不复杂,只是有点繁琐。整个推导过程完全可以按照书上的步骤走一遍即可。
学习资料
首推 pluskid的系列文档阅读:
- 基本篇:
- 支持向量机: Maximum Margin Classifier —— 支持向量机简介。
- 支持向量机: Support Vector —— 介绍支持向量机目标函数的 dual 优化推导,并得出“支持向量”的概念。
- 支持向量机:Kernel —— 介绍核方法,并由此将支持向量机推广到非线性的情况。
- 支持向量机:Outliers —— 介绍支持向量机使用松弛变量处理 outliers 方法。
- 支持向量机:Numerical Optimization —— 简要介绍求解求解 SVM 的数值优化算法。
- 番外篇:
- 支持向量机:Duality —— 关于 dual 问题推导的一些补充理论。
- 支持向量机:Kernel II —— 核方法的一些理论补充,关于 Reproducing Kernel Hilbert Space 和 Representer Theorem 的简介。
- 支持向量机:Regression —— 关于如何使用 SVM 来做 Regression 的简介。

