统计学习方法2：感知机

李航统计学习方法第二章学习笔记 by 沉默的山岭

感知机模型

如下图所示，感知机模型输入是n维向量，输出是 +1、-1二分类。训练数据集线性可分的前提下，感知机模型能找到一个将正例和负例分割开的超平面。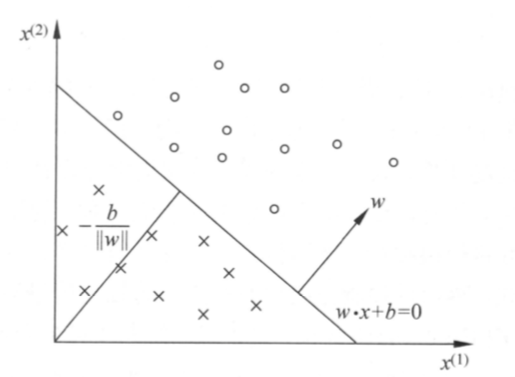

感知机学习策略

损失函数：感知机的损失函数定义为所有误分类点到分割线的距离。总的误分类点的距离为

其中M表示所有误分类点的集合。
为了简化损失函数的优化，这里去掉了了。去掉之后，最小化 仍然能让误分类点数目降低。关于为什么能够去掉这个系数，可以参看支持向量机部分，函数间隔与几何间隔的讨论。
感知机的损失函数为

感知机学习算法

原始形式

感知机的原始形式采用的是随机梯度下降法。 随机梯度下降法的原理，是沿着梯度的方向，随机挑出一个样本对参数更新的方法。相对于梯度下降，随机梯度下降的计算量更小，所以被普遍采用。（缺点是不够健壮，容易受到噪声点的干扰）。
随机梯度法简单推导如下：
步骤一：对损失函数求梯度


步骤二：依据梯度下降后，对于参数的更新只挑选一个样本（随机挑选）进行更新。


反复步骤二，直到训练集中没有误分类点（即所有
为学习率。是0~1之间的超参。

对偶形式

在数学上，对偶问题是指和原问题等价的问题。引入对偶问题，可以把一个难以求解的问题转换为对偶问题进行分析解决。
感知机的对偶形式基本想法，是把w和b表示为样本的线性组合。通过求解线性组合的系数从而求得w和b。分析上述的求解过程，假设w，b初始值为w, b那么对某个误分类点i,我们可能通过执行n次迭代把w和b做了迭代更新, 从而完成了针对该1分类点的迭代，那么


我们假设对于错误的样本，我们都利用上述公式分别进行了迭代。同时假设如果某个样本一直都是未出错样本，那么其n可以取值为0。假设 ，假设w和b的初始值都为0，那么


把上述w的式子带入到损失函数

可以得到一个以a, b为自变量的损失函数

同样求梯度：

随机梯度下降时，我们任意挑选一个分类错误的数据，对其所对应的ak进行更新：


直到未再发现错误的数据点。
对偶形式在迭代中，它只需要更新某个分类错误的样本相关的系数。这个算法的好处在于降低了计算量。