李航 统计学习方法第七章 学习笔记 by 沉默的山岭
一:综述
在跳进支持向量机的细节之前,先来了解熟悉其所需要的数学知识。这部分可以参考书籍的附录C。
对于普通的凸优化问题,解决套路都比较简单,就是求梯度,梯度为零处就是全局最优解。(如果不是凸函数的话,梯度为零处可能是鞍点,也可能是局部最优解,也可能局部最大值)。
拉格朗日对偶性主要是用来求解带约束的优化问题。一般滴,我们可以把要解决的问题描述为:是我们要优化的目标函数,自变量x要满足下面不等式以及等式的约束。
满足下面的等式和不等式约束的所有的x的集合称之为“可行域”。等式和不等式的约束可多可少,可以为零个。但是不等式一定是的形式。(如果原始不等式约束不满足这个形式,稍作变换即可。)如果要得到拉格朗日强对偶性的话,对于
还有进一步的要求的。具体下面再展开。
二、拉格朗日函数的极小极大问题
在上面一节里讨论的优化问题,约束条件和优化的目标函数分散在不同的式子里,很难进行求解。有没有办法把他们合并在一起进行分析研究呢?有的。合并后的结果就是拉格朗日函数。
上述式子里,约束条件前面加的系数称之为拉格朗日乘子(不是🍊)。对于
要求其大于等于0。对于
则没有这个要求。
很明显,这个式子的极值和最初要解决的问题是不等价的。不过如果我们定义一个新的函数:
这个函数意味着x作为自变量可以灵活取值,而每个x对应的,都是拉格朗日函数在各种可能满足条件的
取值后选择出的最大函数值。下角标p的意思是原始问题。
考察这个新的函数,它的可能取值有:
这是因为如果任何一个,那么让对应的
趋于无穷,那么整个函数的值就趋于无穷大。同样如果任何一个
,那么让其对应的
趋于无穷,那么整个函数的值也就趋于无穷大。
如果我们对取极小化,那么它的极值就跟最初要解决的问题的极值是一致的。取到的都是满足原约束的f(x)的最小值。即
和最初要解决的问题等价。我们把称之为广义拉格朗日的极小极大问题。为了下面讨论方便,我们把极小极大问题取得的极值记做:
称做原始问题的最优值。
**
三、极小极大问题与极大极小问题
我们暂时把原来的极小极大问题搁置下。我们来考虑拉格朗日函数的极大极小问题。定义:
然后极大化。得到一个新的问题:
也可将上述问题描述为带约束的优化问题:
我们讲上述问题称作原始问题的对偶问题,并将其极值记做
称为对偶问题的最优值。
**
四、原始问题的最优值和对偶问题的最优值的关系
现在进入了正题,我们来探讨对偶问题的值和原始问题的值到底是什么关系,能否用求解对偶问题替代求解原始问题。
定理C.1 若原始问题和对偶问题都有最优值,则
证明:**
(这步的推导,是因为右边的式子增加了对x可行域的约束,因此得到的极小值有可能更小。)
(上面这步的推导,是因为既然x在可行域中,也就是说最初问题的哪些约束成立,那么就为0,可去掉。而
是个非正项,因此去掉后最小值会放大。)
上面这步推导,是因为内部最小化的函数中既然已经不包含,那么就可以去掉外部的的运算。去掉后的式子,就是最初问题的定义,它的最优值就是原始问题的最优值。
这个证明是视频中讲解的证明方法,书本上的证明看不太懂。特别是C.16取极大值的时候附加了约束,为什么仍然能推导出是一次放大?总感觉不太充分。
定理C.1的意义在于给出了原始问题的一个下界,即原始问题的最优值不可能小于。
从上面论证可以知道。那何时等号成立呢?
等号成立的充分条件是:
凸优化问题 = { f(x)是凸函数,且可行域是一个凸集 (集合中的两点之间的连线仍然属于该集合,那么该集合就是凸集) }
如果我们原始问题中的约束条件里,是凸函数,而
是仿射函数(线性函数)时,对应确定出的可行域就是一个凸集。(依然是充分条件,不是充要条件)。
Slater条件:要求可行域不但是一个凸集,而且凸集是要有内点的。(不能是一个点或者一条线构成的凸集)
在满足上述条件的情况下,定理C.2成立,也就是说,。而
就是取得 最优值时的自变量取值。
定理C.3给出了KKT条件,当对偶问题具有强对偶性时(KKT成立的前提),对应最优解的充要条件就是KKT条件,即:
最后一个条件也叫互补松弛条件。意味着系数和不等约束条件必须有一个为零。
关于定理C.2和C.3,书中没有给出证明。可以参考学习资料中的文档进行直观理解。
这里我也做了几个图形来辅助直观理解下带约束的优化问题。制图工具使用的是 [_https://www.geogebra.org/3d](https://www.geogebra.org/3d)
目标优化函数是 。该函数在三维坐标轴图形如下:
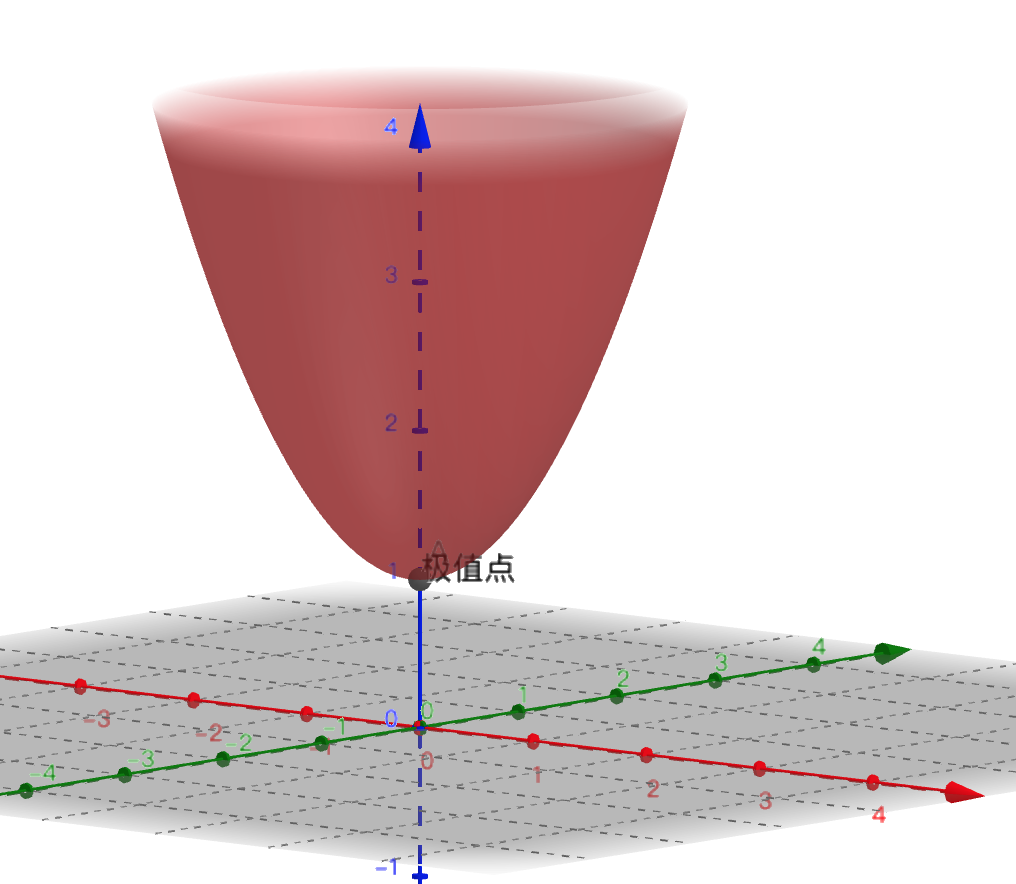
很明显,函数在最低点,梯度为零处取得了极小值。 无约束下凸函数的最优化取梯度为零处即可。
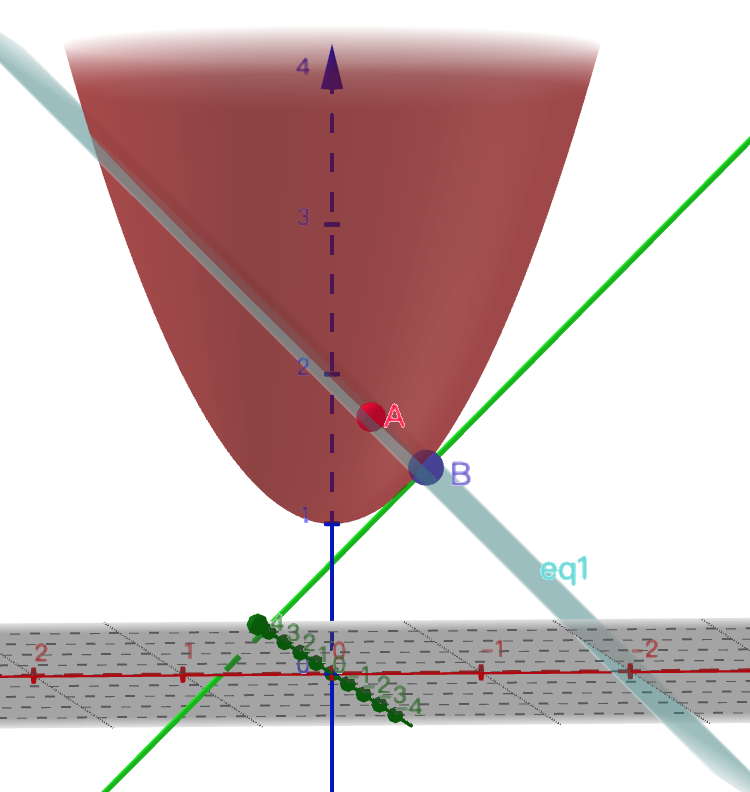
附加上一个约束仿射函数,z-x-2=0 之后,极值点就不在原来的地方了。那么在哪里呢?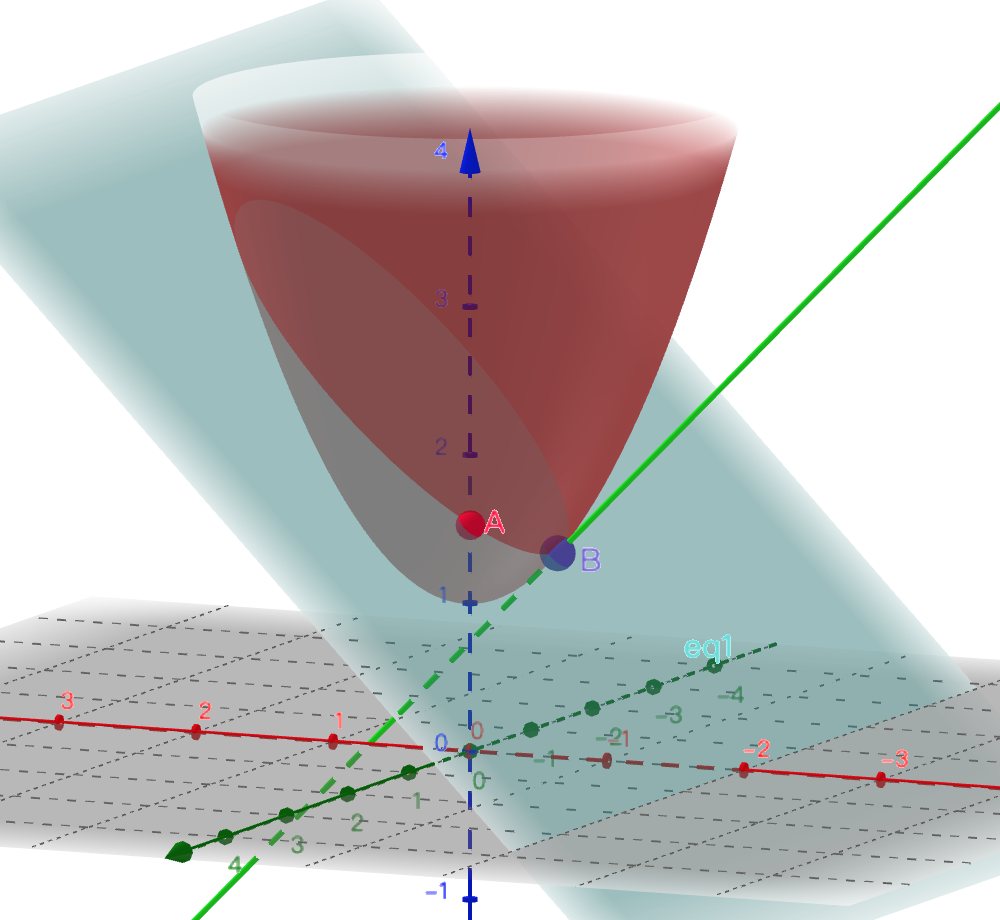
从这张图里我们能看出来,受约束的极值点首先肯定在平面上(必须满足约束条件),其次,必须在目标函数的曲面上。那么它会是类似于点A的地方吗?肯定不会。因为明显点B取得的极值要更低。那么点B有何特殊之处呢?我们可以把图形旋转一个方向来观察就很清楚了。
点B处,目标函数的梯度和约束函数的梯度是相反的(梯度指向函数增长最快的方向。把这个方向投影到x,y轴的平面上,就是梯度的方向。)。
换个思路,如果有两股力量作用在同一个物体上,当这个物体静止的时候,这两股力量一定是相互抵消的。否则这两股力量的合力会推动这个物体一直运动,直到达到平衡为止。按这个思路解释,那么 这个式子的由来就比较容易理解了。
参考
关于拉格朗日和KKT介绍,可以参考马同学的阐述: