统计学习方法7_3：核方法专题

李航 统计学习方法 第七章 学习笔记 by 沉默的山岭

综述

核方法是把线性算法扩展为支持非线性数据集的一种技巧。这种技巧在其他地方常常也可以看到它的踪影。课本上对于核方法的阐述的思路是从给定的核函数出发，找到这个核函数对应的希尔伯特空间，并证明核函数等价于希尔伯特空间中的点乘。个人感觉比较难于消化，因此阅读Changyue Song所做的两篇文章并做了阅读笔记。原文参加文末链接。

函数空间与函数的点乘

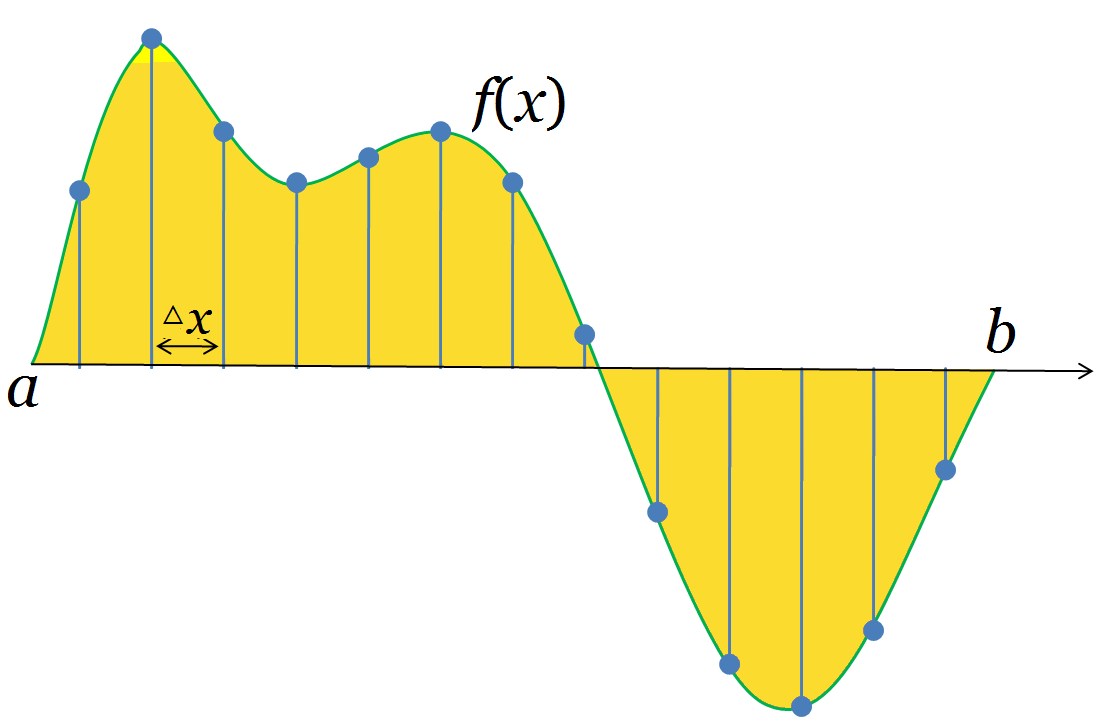
假设我们把f(x)中的每一个可能的取值点都列出来并放入一个向量，我们就得到了一个等价于函数的无穷维向量。两个无穷维向量之间的点积，可以这样定义：

和向量空间一样，一组正交（点积为零）的函数向量能够张成一个函数空间。这组正交的函数向量就是这个函数空间的正交基。而这个空间中的所有函数能由这组基线性表出。
傅里叶变换就是一个例子。傅里叶变换的基函数(sinnx, cosnx)相互之间是正交的，且能够线性组合表出所有的周期函数。

低维到高维

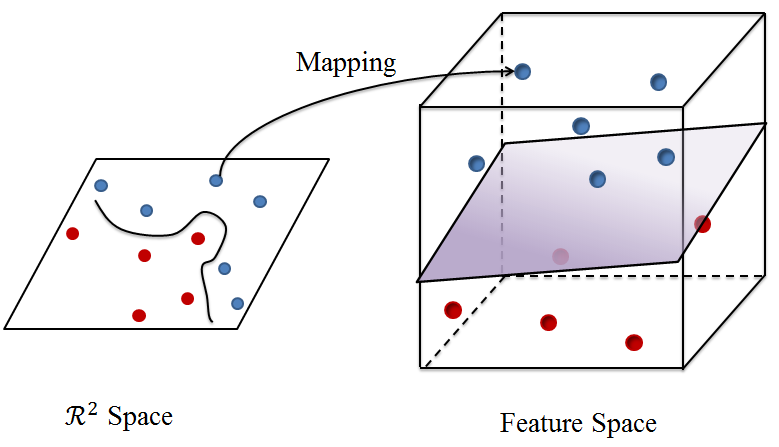
低维度空间里非线性可分的集合，在高维度空间里很可能是线性可分的。问题在于，如何找到一个这样的高维空间？核方法给出的答案就是能根据核函数找到这样的一个高维空间。

矩阵的特征分解

对于一个实对称矩阵 ，存在一个实数 ,以及向量 使得下式成立：

那么 称为矩阵 的特征值，称为该矩阵的特征向量。有n个特征值以及对应的特征向量，且特征向量之间两两正交（点积结果为零）。
矩阵可以被分解为下面的式子：

这里是正交矩阵，即(单位矩阵) ，是对角矩阵。如果我们把表示为列向量的形式，则有

综上，我们有



是空间的一组正交基。

核函数

我们之前说过，一个函数可以认为是一个无穷维向量。那么，上述的矩阵分解的思路，是否也可以用来研究函数呢。答案当然是 “是”。一个函数能够被分解研究的充分条件（Mercer核函数条件）是对称且（半）正定。即：
，且

则该函数能够充当核函数。

对于核函数，同样存在特征值和特征函数，使得下式成立：

而正交的函数点积同样为零

对于一个核函数，存在无数个相互正交的特征函数以及对应的特征值，使得下式成立：

再生希尔伯特空间

假设是希尔伯特空间的一组正交基。那么，以这组基表出的希尔伯特空间中的函数有两种表达方式。我们可以把它表达为基的线性组合：

也可以表示为一个无限维度向量。（注意，表达为向量时，向量的每个分量是对应的维度下的坐标，因此不需要乘以基，只需要把该基底下的坐标写出。）

这两种方式是等价的。
假如有另外一个函数 。那么

好，铺垫完之后回到正题。对于核函数，我们用 代表核函数具体的一个值，为标量。用代表 函数（或者说无限维度矩阵）本身。用代表矩阵的第行，或者说我们把第一个参数固定为，把它都做是一个单参数的函数，或者无限维向量。根据上面铺垫的推论，按线性组合的方式，我们有

如果表示为向量，则为 （去掉基）

因此

假如我们令

它就代表了从低维空间往高维空间的一个映射。而：

这样我们就达到了目的，两个高维空间的点积被一个在低维空间的核函数表达了出来。如果我们能够把高维空间里的所有运算都限定在点积范围内的话，那么我们是不需要知道映射用的，也不需要构造特征空间，只需要找到一个合适的核函数就好了。

常用核函数

网上类似信息很多，不再重复了。常用核函数搜索结果

参考

Changyue Song博客

A Story of Basis and Kernel - Part I: Function Basis A Story of Basis and Kernel - Part II: Reproducing Kernel Hilbert Space