李航统计学习方法第一章习题 by 沉默的山岭

作业准备

伯努利模型

伯努利试验（Bernoulli experiment）是在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。我们假设该项试验独立重复地进行了n次，那么就称这一系列重复独立的随机试验为n重伯努利试验，或称为伯努利模型。经常用来举例的n次掷硬币试验，就是一种伯努利模型。
在伯努利模型中，可以引申出三种常见的概率分布：二项分布，几何分布，贝塔分布

二项分布

在上述伯努利试验中，事件（取值为1）的发生次数为k次。我们认为事件发生k次服从参数为的二项分布。

二项分布的期望为 。方差为。
二项分布有时会约定简单记为

几何分布

在上述伯努利试验中，事件（取值为1）的在第k次试验中首次发生。换言之前面都取值为0，在第k次取值为1。我们认为事件在第k次发生服从参数为的几何分布。

几何分布的期望为。方差为。

概念：共轭先验分布

在贝叶斯统计中，如果后验分布与先验分布属于同类，则先验分布与后验分布被称为共轭分布，而先验分布被称为似然函数的共轭先验。
在上述伯努利试验中，其似然函数是二项分布，而其先验分布依据人们的主观经验给出，通常会以以贝塔分布的形式给出。而贝塔分布正是二项分布的共轭先验，贝塔分布对应的后验分布依然是贝塔分布。

贝塔分布(B分布，分布）

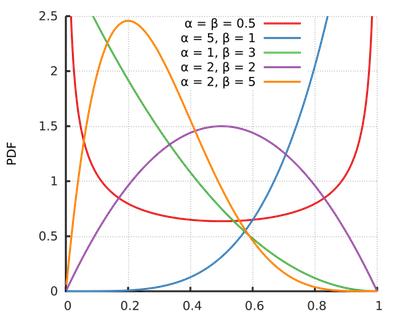
beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。上面的图形中，包含了5中不同参数的beta分布的概率密度函数。可以观察到，beta分布的概率密度函数可以用“变化多端”来形容。唯一确定的是：其定义域在0-1之间，对其积分结果为1.（因为它是概率的概率）。
因为贝塔分布自带归一化，因此参数的绝对值的大小不影响贝塔分布，真正起作用的是两个参数相对差异。所以贝塔分布从先验更新为后验的方法很简单，只要把对应的成功次数和失败次数叠加到两个参数中去，就获得了更新过的后验分布。
贝塔分布的概率密度函数为

其中，B(a,b)为贝塔函数。a,b为预先给定的常数。 为函数的自变量。

所以我们也可以把B函数看做是保证Beta分布成为一个概率分布（积分为1）的normalize项。

似然与概率

在进行极大似然估计之前，先来了解下什么是似然，什么是概率。
知乎专栏有两篇讲解的非常好：极大似然简介 以及 贝叶斯统计学简介。下面的内容主要来自于这两篇专栏文章。

不管是极大似然估计，还是贝叶斯估计，都是统计推断的一种。统计推断，或者叫做推断统计学（statistical inference）是指统计学中研究如何根据样本数据去推断总体数量特征的方法。统计推断主要可以分为两大类：一类是参数估计问题；另一类是假设检验问题。 统计推断的任务，就是根据样本去作出某种关于总体的未知参数的概率形式的论断。比如对未知参数 的值作一个估计或者判断 的区间。 统计推断可能使用如下三种信息： 一 总体信息，即总体分布或所属分布族的信息。 二 样本信息，即从总体抽取的样本的信息。 三 先验信息，即在抽样之前有关统计问题的一些信息，主要来源于经验和历史资料。

贝叶斯学派和频率学派的主要区别在于是否引入先验信息。 只使用第一种和第二种信息进行的统计推断被称为经典统计学，也叫做频率学派，它的基本观点是把数据（样本）看成是来自具有一定概率分布的总体，所研究的对象是这个总体而不限于数据本身。 基于上面三种信息进行的统计推断叫做贝叶斯统计学。它和频率学派的主要差别在于是否利用先验信息。贝叶斯统计学对先验信息的收集挖掘和加工，使其数量化，形成先验分布，提高统计推断的质量。

极大似然是什么 设总体分布为 ， 是从总体分布中抽出的样本， 假设样本之间的独立性，那么样本() 的联合分布为： 当固定 时，把L看作是以 变量的函数时，L是一个概率密度函数。 当固定 时， 把 L 看作是以 为变量的函数，由于 是确定值（是变量但非随机变量）（按频率学派观点）。这时L不能叫做概率（因为不具有不确定性），叫做似然（likelihood）。 使得likelihood最大的那个点记为： 并将其并作为 的估计值(频率学派，点估计中的一种)，在已有的样本 条件下， 就叫做 的极大似然估计。 由于 且为了使得L最大，只须使得log L 最大，故在f对存在连续偏导数时，可以建立方程： 如果有多个参数就针对每个参数联立方程组： 如果这个方程组有唯一的解，且有能验证它是一个极大值点，那么它必定是使L达到最大的点，即极大似然估计。

习题一：极大似然估计与贝叶斯估计

题目：说明伯努利模型的极大似然估计以及贝叶斯估计中的统计学习方法三要素。伯努利模型是定义在取值为0或1的随机变量上的概率分布。假设观测到的伯努利模型n次独立的数据生成结果，其中k次的结果为1，这时可以用极大似然估计或贝叶斯估计来估计伯努利模型中，取值为1的概率（模型参数）。

极大似然估计

掷硬币模型中，我们的目标是建立一个对下一次掷硬币结果的预测。模型本身为二项分布，需要学习的是参数,代表正面朝上的概率。

我们假设第i次结果为

某次投掷结果的概率为
给定下，样本集的似然函数为

最大化似然函数等同于最大化对数似然函数。因此

对求导数，并取导数为零的极值点：


如果有k次正面朝上，那么有

极大似然估计的三要素为:
模型：模型为二项分布，其参数为,代表正面朝上的概率。该概率未知，需要学习获得。
策略：损失函数为对数似然损失。极大化对数似然函数，等同于极小化对数似然损失。
算法：算法比较简单，通过求导直接求极值。

贝叶斯估计

贝叶斯学派的最基本的观点是：任何一个未知量 都可以看作一个随机变量，应该使用一个概率分布去描述 ，这个概率分布是在抽样前就有的，被称为先验分布。

进行贝叶斯估计前，需要首先假设一个先验分布。Beta分布经常作为概率的先验分布使用，因此我们也选择Beta分布作为先验。关于Gamma函数，Beta函数暂时不展开，可以参考这里：理解Gamma分布、Beta分布与Dirichlet分布以及它的参考文献。
贝塔分布的概率密度为：。实际使用中，通常需要先给定a,b一个值作为先验知识。这里暂时不指定，当做一个常数。
根据贝叶斯公式：

这里先验分布取Beta分布，有：

把贝塔分布带入最上面的式子，然后把似然函数也代入

因为我们要求使得后验分布最大化的，因此和无关的项并没有那么重要。抛去不含的系数，上面的式子可以正比于：
原式子：

从上图看，得到的后验分布仍然是一个beta分布，其分布参数为（）。我们可以取beta分布的众数（就是概率密度函数中概率最大的点）作为对的估计。已知参数为（a, b)的beta分布的众数为：。那么上述后验分布的众数为：。
然后我们就可以拿这个式子作为对的估计。

贝叶斯估计的三要素为:
模型：模型为条件概率分布，其参数为,代表正面朝上的概率。该概率未知，需要学习获得。
策略：损失函数为对数似然损失。除了考虑训练集的损失，还引入了先验分布作为规范化方式。（增加了一个先验分布作为惩罚项。
算法：算法比较简单，通过求导直接求极值。

习题二：经验风险最小化与极大似然估计

对照对数损失函数和上面极大化似然函数的计算过程，可以发现极大化似然函数，就是在极大化负的对数损失。因此以对数损失作为损失函数，最小化经验风险等价于极大似然估计。

参考链接

如何理解贝叶斯推断和beta分布
Understanding the beta distribution (using baseball statistics)
Beta分布深入理解 （TODO)
极大似然简介
贝叶斯统计学简介
理解Gamma分布、Beta分布与Dirichlet分布 （TODO)

数学函数图像：

第一个：Desmos
第二个：fooplot