1 伸展树(Splay tree)

平衡二叉搜索树有诸多变种，除了上一章讲的——AVL树之外，以下将介绍其中几位成员。首先，鉴于数据访问的局部性在实际应用中普遍存在，按照最常用者优先的策略引入伸展树。接下来，通过对平衡二叉树的推广，引入平衡多路搜索树，并着重讨论其中比较典型的B树。对照4阶B树，引入红黑树，红黑树不仅仅能保证全树的适度平衡，从而有效地控制单次操作的时间成本并可将每次重平衡操作的时间复杂度控制在常数时间范围内。

1 伸展树(Splay tree)

伸展树和AVL树一样，也是平衡二叉搜索树的一种形式。相对于AVL树，伸展树无需时刻都保持全树的平衡，但却可在任何足够长的真实操作序列中保持分摊意义上的高效率。伸展树也不需要对基本的二叉树节点结构做任何附加要求或改动，更不需要记录平衡因子或高度之类的额外信息，故适用范围更广。

1.1 伸展树的局部性

为考查和评价各操作接口的效率通常假设所有操作彼此独立、次序随即且概率均等，并从平均情况的角度出发。实际上，通常在数据的生命期内，不仅执行不同操作的概率往往极不平衡，而且各操作之间具有极强的相关性，并在整体上多呈现极强的规律性。其中最典型的为数据局部性，即：

刚刚访问的元素，极有可能在不久之后被访问到
将被访问的某个元素，极有可能就处于不久之前被访问过的某个元素附近

可利用“即用即前移”的启发式策略，将最为常用的数据项集中于列表的前端，从而使得单次操作的时间成本大大降低。同样的，类似的策略也可应用于二叉搜索树。

就二叉搜索树而言，数据局部性具体体现为：

刚刚被访问的元素，极有可能在不久之后被访问到
将被访问的某个元素，极有可能就处于不久之前被访问过的某个元素附近

因此，只需将刚被访问的节点，及时的“转移”至树根（附近），即可加速后续的操作。

当然，转移前后的搜索树必须相互等价，故仍需借助 chapter7的 3.1 等价变换中的技巧。

1.2 逐层伸展

这是一种直接的方法：每访问过一个节点之后，随即反复地以它的父节点为轴，经适当的旋转将其提升一层，直至最终成为树根。

以图8.1为例，若深度为3的节点E刚被访问——无论查找或插入，甚至“删除”——都可通过3次旋转，将该树等价变换为以E为根的另一棵二叉搜索树。

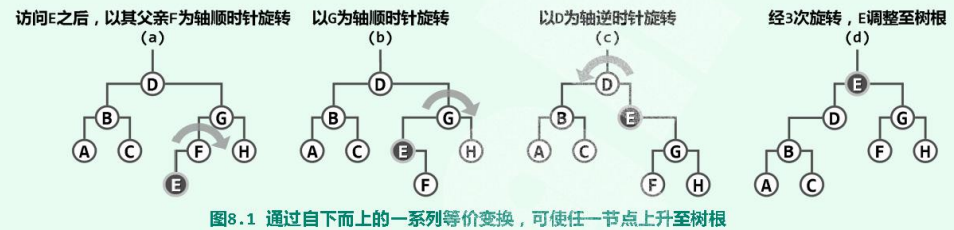
随着E节点的逐渐上升，两侧子树的结构也不断地调整，故这一过程也形象地称作伸展树(splaying)。

但是，目前的策略存在致命的缺陷——对于很多访问序列，单词访问分摊时间复杂度在极端情况下可能高达 chapter8.1 伸展树 - 图3 （如下图所示）。

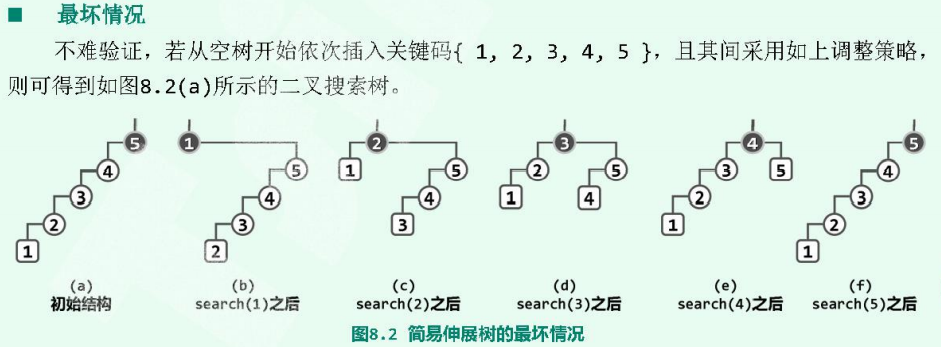
此时，若通过search接口，再由小到大的依次访问各节点一次，则该树在歌词访问之后的结构形态将如上图(b~f)所示。
可见，在歌词访问之后，为将对应节点伸展调整至树根，分别需要做4、4、3、2、1次旋转。一般地，若节点总数为 chapter8.1 伸展树 - 图5 ,则旋转操作的总次数应为： chapter8.1 伸展树 - 图6

如此分摊下来，每次访问平均需要 chapter8.1 伸展树 - 图7 时间。这一效率不仅远远低于AVL树，甚至与原始的二叉搜索树相当。以上例子在经过5次访问后全树的结构将会复原，这意味着以上情况可以持续地再现。

若其推广至规模任意的二叉搜索树，对于规模为任意n的伸展树，只要按照关键码单调的次序，周期性地反复进行查找，则无论总的访问次数m>>n有多大，就分摊意义而言，每次都需要 chapter8.1 伸展树 - 图8 时间。

所以，实现真正意义上的伸展树，我们还需要对以上的逐层伸展策略进行微调。

1.3 双层伸展

以上单层伸展的问题在于全树的拓扑结构始终呈单链表结构，等价于一维列表。被访问节点的深度，呈周期性的算术级数演变 chapter8.1 伸展树 - 图9

为了克服上述伸展调整策略的缺陷，可将逐层伸展改为双层伸展：**每次都从当前节点v向上追溯两层而不是一层，并根据其父节点p和祖父g的相对位置进行相应的旋转**。

旋转的情况分为三种：

1.3.1 zig-zig/zag-zag（关键所在）

逐层伸展的 关键所在。

设v是p的左孩子，且p也是g的左孩子，设W和Y分别是v的左、右子树，Y和Z分别是p和g的左、右子树。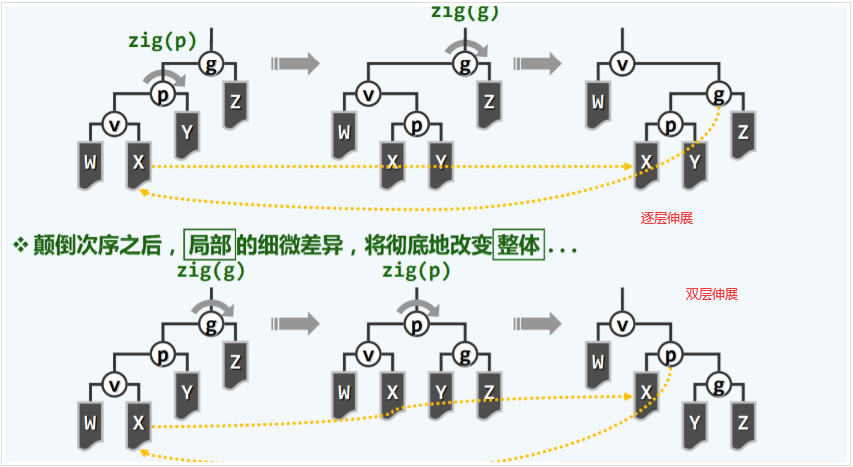
一旦访问坏节点，对应的路径的长度随即减半。

具体步骤：

首先，以g为轴，做顺时针旋转zig(g)；
然后，再以P为轴做顺时针旋转zig(p)；

如此，连续两次的zig旋转，合成zig-zig调整。对称的，zag-zag操作，也类似，区别只是旋转方向为zag旋转。

注意，与chapter7 中4.2.2.1 单旋的区别。

1.3.2 zig-zag/zag-zig

设v是p的左孩子，而p是v的右孩子，设W是g的左子树，X和Y分别是v的左、右子树Z是p的右子树。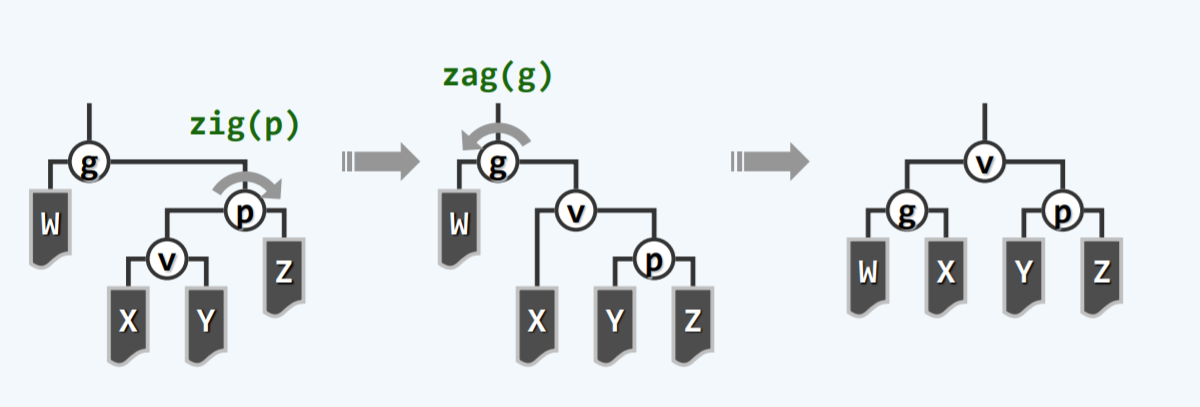 chapter8.1 伸展树 - 图11
具体步骤：

首先，以节点p为轴，做顺时针旋转zig(p)；
然后，再以g为轴做逆时针旋转zag(g)；

如此，连续两次的zag旋转，合成zig-zag调整。对称的，zag-zig操作，也类似，区别只是旋转方向先为zag旋转，后为zig旋转。

与chapter7 的4.2.2.2 双旋是一样的。

即：zig-zig/zag-zag：调整与此前的逐层伸展完全一致。（而且与之前AVL的双旋调整也一样）。

1.3.3 zig/zag

这种情况是由于，当v最初的深度为奇数，则经过若干次双层调整之后，v的父亲p即是树根r。将v的左右子树记作X和Y，节点p=r的另一子树记作Z。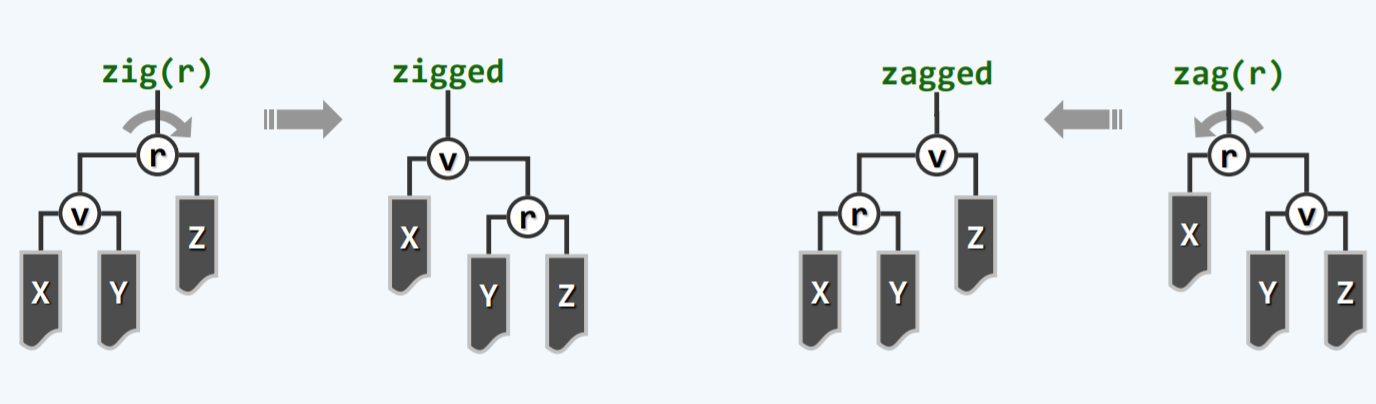
chapter8.1 伸展树 - 图12
调整过程，就类似于“逐层伸展”的一次伸展。

1.3.4 效果与效率

综合以上情况，每经过一次双层调整操作，节点v都会上升两层。

若v的初始深度depth(v)为偶数，则最终v将上升至树根。
若depth(v)为奇数，则当vv上升至深度为1时，不妨最后再相应地做一次zig或zag单旋转操作。

无论如何，经过depth(v)次旋转后，v总能成为树根。

在逐层伸展中的最坏情况导致 chapter8.1 伸展树 - 图13 平均单次访问时间的原因为：在这一可持续重复的过程中，二叉搜索树的高度始终不小于 chapter8.1 伸展树 - 图14 ，而且至少有一半的节点在接受访问时没有如预期地靠近树根，反而恰恰处于最底层。从树高的角度来看，树高依算术级数逐步从 chapter8.1 伸展树 - 图15 递减至 chapter8.1 伸展树 - 图16 ，然后再逐步递增地增回到 chapter8.1 伸展树 - 图17 。

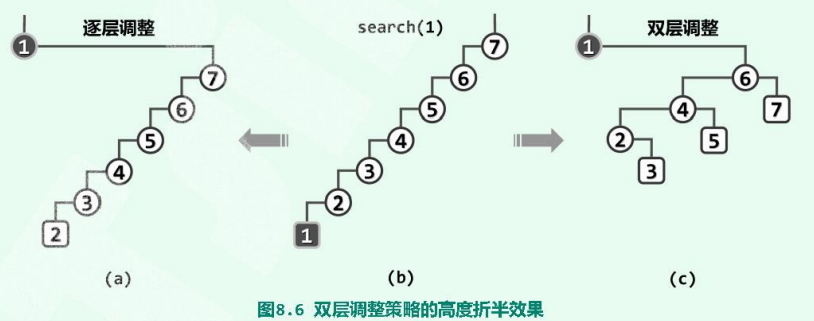
以以上二叉搜索树为例，逐层调整和双层调整的区别如图所示。

逐层伸展时，最深节点在经过双层调整后，不仅同样可将该节点伸展至树根，而且可使树的高度接近于减半，可有效避免对长分支的访问。在将节点v调整至树根的同时，对应分支长度以几何级数的速度(大致折半)收缩。

在任一时刻伸展树中都可能存在很深的节点，但是经过随后的双层伸展，其对应的分支长度都会收缩至长度大致这般，最坏情况也不会持续发生。可见，伸展树虽不能杜绝最坏情况，却能有效地控制最坏情况发生的频率，从而在分摊意义上保证整体的高效率。

在改用“双层伸展”策略之后，伸展树的但此操作均可在分摊复杂度为 chapter8.1 伸展树 - 图19 的时间内完成。

1.4 伸展算法(`splay`)的实现

/*********************************伸展算法的实现***********************************/
template<typename NodePosi> //在节点*p与*lc（可能为空）建立 “父（左）子”关系
inline void attachAsLChild(NodePosi p, NodePosi lc)
{
    p->lc_ = lc;
    if (lc)
        lc->parent_ = p;
}
template<typename NodePosi> //在节点*p与*rc（可能为空）建立 “父（右）子”关系
inline void attachAsRChild(NodePosi p, NodePosi rc)
{
    p->lc_ = rc;
    if (rc)
        rc->parent_ = p;
}
template<class T> //splay树伸展算法：从节点v出发逐层伸展
BinNodePosi<T> Splay<T>::splay(BinNodePosi<T> v)
{
    //由于使用双层伸展，所以先找到v的父亲p、祖父g（此时需要v节点不空）
    if (v == nullptr)
        return nullptr;
    BinNodePosi<T> p = v->parent_;
    BinNodePosi<T> g = p->parent_;
    while (p && g) //在v的每一次双层伸展时，要确保v的每一次的父亲、祖父是存在的
    {
        BinNodePosi<T> gg = g->parent_; //每轮之后*v都以原曾祖父（great-grand parent）为父亲
        if (IsLChild(*p)) //zig
        {
            if (IsLChild(*v)) //zig-zig
            {
                attachAsLChild(g, p->rc_);    attachAsRChild(p, g);
                attachAsLChild(p, v->rc_);    attachAsRChild(v, p);
            }
            else //zig-zag
            {
                attachAsLChild(p, v->rc_);    attachAsRChild(v, p);
                attachAsRChild(g, v->lc_);    attachAsLChild(v, g);
            }
        }
        else if (IsRChild(*p)) //zag
        {
            if (IsRChild(*v)) //zag-zag
            {
                attachAsRChild(g, p->lc_);    attachAsLChild(p, g);
                attachAsRChild(p, v->lc_);    attachAsLChild(v, p);
            }
            else //zag-zig
            {
                attachAsRChild(p, v->lc_);    attachAsLChild(v, p);
                attachAsLChild(g, v->rc_);    attachAsRChild(v, g);
            }
        }
        //完成一次双层伸展之后，需要将*v与*gg建立联系
        if (!gg)    v->parent_ = nullptr; //*v的原先的曾祖父*gg不存在，则说明，此时*v应为树根
        else //否则，*gg此后应该以*v作为左or右孩子
        {
            (g == gg->lc_) ? attachAsLChild(gg, v) : attachAsRChild(gg, v);
        }
        updateHeight(g); updateHeight(p); updateHeight(v); //每轮都更新一下节点g、p、v的高度
    } /*到此为止，双层伸展结束，且此时的g节点彼等于null，p有可能存在原因是：
      * 因为此时已经完成双层伸展，也就是说，v上面的节点不能再构成“v,p,g”这三个节点了，此时
      * 可以肯定的是g节点肯定是空的，而p节点有可能存在：
      * 1. 如果当初v最初的深度为奇数，那么此时p是存在的；
      * 2. 如果为偶数，那么p不存在，此时v就在树根的位置
      * 具体可看：https://www.yuque.com/longlongqin/xkqqbk/xzo2yd#VIlCh
      */
    if (p = v->parent_) //当p非空是，还需要一次 zig/zag
    {
        if (p->lc_ = v) //v是p的左子树
        {
            attachAsLChild(p, v->rc_);
            attachAsLChild(v, p);
        }
        else //v是p的右子树
        {
            attachAsRChild(p, v->lc_);
            attachAsLChild(v, p);
        }    
        updateHeight(p); updateHeight(v);
    }
    v->parent_ = nullptr; //最后，v是树根，所以它的父亲为空
    return v;
} //调整之后心术跟应为被伸展的节点，故返回该节点的位置一边上层函数更新树根

1.5 伸展树的“查找”

查找算法，与之前AVL树不同点在于：

首先调用二叉搜索树的searchIn()，查实查找具有关键码e的节点；
然后，看查找的结果：
- 查找成功，则将查找到的节点，调用splay()算法，将其伸展到树根；
- 查找失败，则将查找失败的hot_节点，调用splay()算法，将其伸展到树根；

也就是说，无论失败还是成果，都继续调用splay()算法，将查找到终止位置处的节点伸展到树根。

/*********************************查找***********************************/
template<class T>
BinNodePosi<T>& Splay<T>::search(const T& e)
{
    BinNodePosi<T> p = searchIn(root_, e, hot_ = nullptr);
    root_ = splay(p ? p : hot_); //如果查找成功，则p非空；失败，则p为空
    /*
    * 1. 查找成功，则将查找到的节点，调用splay()算法，将其伸展到树根；
    * 2. 查找失败，则将查找失败的hot_节点，调用splay()算法，将其伸展到树根；
    */
    return root_;
} //与其它BST不同，无论查找成功与否，_root都指向最后被访问的节点

1.6 伸展树的“插入”

由于Splay::search()已经集成了splay()伸展功能。所以，查找返回后，

树根节点要么等于查找目标（查找成功），
要么就是hot_，而且恰为拟插入节点的直接前驱或直接后继（查找失败）。

因此不妨改用如下方法实现Splay::insert()接口。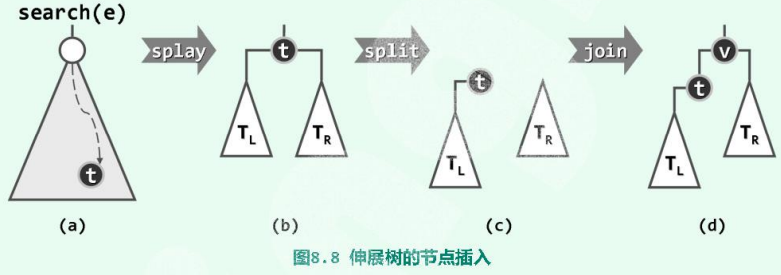

具体插入过程：

为将关键码e插至伸展树T中，首先调用伸展树查找接口Splay:: search(e)，查找该关键码（图(a)）。
于是，其中最后被访问的节点t，将通过伸展被提升为树根，其左、右子树分别记作TL和TR（图(b)）。
接下来，根据e与t的大小关系(不妨排除二者相等的情况），以t为界将T分裂为两棵子树。
- 比如，不失一般性地设e大于t。于是，可切断t与其右孩子之间的联系（图(c)）。
再将以e为关键码的新节点v作为树根，并以t作为其左孩子，以TR作为其右子树（图(d)）。

v小于t的情况与此完全对称。

/*********************************插入***********************************/
template<class T>
BinNodePosi<T> Splay<T>::insert(const T& e)
{
    if(root_ == nullptr) //原树为空时
    {
        size_++;
        return root_ = new BinNode<T>(e);
    }
    if (e == search(e)) //如果将要插入的关键码已经存在，则直接返回
        return root_; //因为查找之后，会进行伸展，所以被查找的节点会被伸展到根节点处
    BinNodePosi<T> t = search(e); ++size_; //创建新节点
    if (e > t->data_) //t作为v的左孩子
    {
        BinNodePosi<T> v = new BinNode<T>(e); //插入新的根节点，此根节点以e为关键码的新节点v作为树根
        t->parent_ = v;
        v->lc_ = t;
        v->rc_ = t->rc_;
        t->rc_ = nullptr;
    }
    else if (e < t->data_) //t作为v的右孩子。【这里存在 e = t->data_，因为包含在了if (e == search(e)) 中】
    {
        BinNodePosi<T> v = new BinNode<T>(e);
        t->parent_ = v;
        v->lc_ = t->lc_;
        v->rc_ = t;
        t->rc_ = nullptr;
    }
    updateHeightAbove(t); //更新t及其祖先（实际上只有t一个）的高度
    return root_; //新节点v（v就是根节点）必然位于根节点处
} //无论e是否存在原树中，返回时总有root_->data_ = e

尽管伸展树并不需要记录和维护节点高度，为与其它平衡二叉搜素树的实现保持统一，这里还是对节点的高度做了及时的更新。出于效率的考虑，实际应用中可视情况，省略这类更新。

1.7 伸展树的“删除”

同样地，在实施删除操作之前，通常都需要调用splay::search()定位目标节点，而该接口已经集成了splay()伸展功能，从而使得在成功返回后，树根节点恰好就是待删除节点。
因此，亦不妨改用如下策略，以实现splay::remove()接口。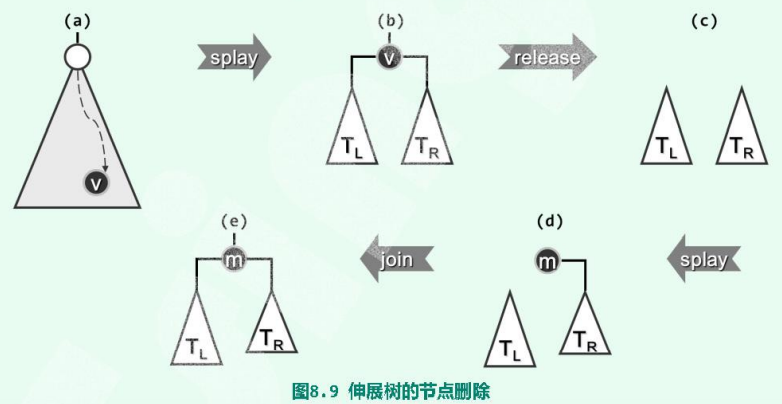

具体删除过程：

为从伸展树T中删除关键码为e的节点，

首先亦调用接口splay::search(e)，查找该关键码，且不妨设命中节点为v（图(a)）。
于是，v将随即通过伸展被提升为树根，其左、右子树分别记作T和TR(图(b)）。
接下来，将v摘除（图(c)）。此时需要分情况讨论：
- 1. 当此时的树，没有左子树 or 没有右子树，则可直接删除将v删除。就可以了；
- 1. 当此时的树，左右孩子均存在，就需要：在TR中再次查找关键码e。尽管这一查找注定失败，却可以将TR中的最小节点m，伸展提升为该子树的根。得益于二叉搜索树的顺序性，此时节点m的左子树必然为空；同时，TL中所有节点都应小于m (图(d)）。
情况2之后，于是，只需将TL作为左子树与m相互联接，即可得到一棵完整的二叉搜索树(图(e))。

如此不仅删除了v，而且既然新树根m在原树中是v的直接后继，故数据局部性也得到了利用。

当然，其中的第二次查找也可在TL（若非空）中进行。

/*********************************删除***********************************/
template<class T>
bool Splay<T>::remove(const T& e)
{
    if (!root_ || e != search(e)->data_) //当树为空 or 目标不存在，则返回false
        return false;
    BinNodePosi<T> v = root_; //经search() 后节点e已被伸展值树根
    if (!root_->lc_) //如果没有左子树，则可直接删除
    {
        root_ = root_->rc_;
        root_->parent_ = nullptr;
    }
    else if (!root_->rc_) //如果没有右子树，则也可直接删除
    {
        root_ = root_->lc_;
        root_->parent_ = nullptr;
    }
    else //左右子树均存在
    {
        //先暂时将左子树切掉（对称的，在本次查找中(第二次) 你也可以暂时将右子树切掉）
        BinNodePosi < T> LTree = root_->lc_; LTree->parent_ = nullptr; //先暂存一下左子树
        root_ = root_->rc_; //原树根节点记录在v中
        root_->parent_ = nullptr;
        search(e); //还是以e为关键码进行第二次查找（此次查找必然失败）
        //至此，右子树中最小节点必伸展至根，且（因无雷同节点）其左子树必空，于是
        root_->lc_ = LTree; LTree->parent_ = root_; //只需将原左子树接回原位置即可
    }
    release(v->data_); release(v); --size_; //释放节点、更新规模
    if (!root_) //此后，若树非空，则需更新树根的高度
        updateHeight(root_);
    return true; //返回成功标志
} //若目标节点存在且被删除，返回true；否则返回false

chapter8.1 伸展树