下面来看，fibonacci数的 二分递归的实现：
image.png
由此定义，可直接写出如下递归形式的代码：

  1. int64_t fib(int n)
  2. {
  3.     return (n>2)?
  4.         (int64_t)n
  5.         : fib(n-1) + fib(n-2);

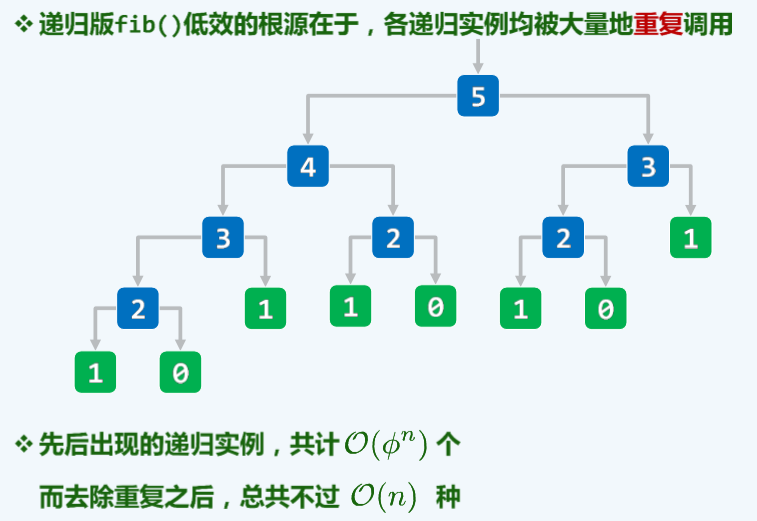
image.png

优化

为了消除递归算法中重复的递归实例。一种自然而然的思路和技巧，可以概括为：
借助一定量的辅助空间，在各子问题求解之后，及时记录下其对应的解答。

有两种方法：

  • 可以从原问题出发 自顶向下，每当遇到一个子问题，都首先检查它是否已经计算过，以期通过直接调阅记录来获得解答，从而避免重新计算。——这种是：制表（tabulation）或记忆（memoization）策略。
  • 也可以从递归基出发，自底而上 递推的得出各子问题的解，直至最终原问题的解。——这种是：动态规划（dynamic programming）策略。


线性递归

image.png

迭代——动态规划

反观以上线性递归版fib( )算法可见，其中所记录的每一一个子 问题的解答，只会用到一次。在该算法抵达递归基之后的逐层返回过程中，每向上返回一层，以下各层的解答均不必继续保留。

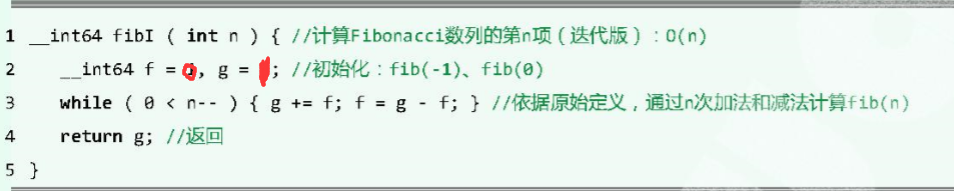
若将以上逐层返回的过程，等效地视作从递归基出发，按规模自小而大求解各子问题的过程，即可采用动态规划的策略，将以上算法进一步改写为如下所示的迭代版。
image.png