5. 编码树

5.1 二进制编码

在加载到 信道 上之前，信息被转换为二进制形式的过程称作 编码(endcoding)；
反之，经信道地道目标后再由二进制编码恢复原始信息的过程称作 解码(decoding)。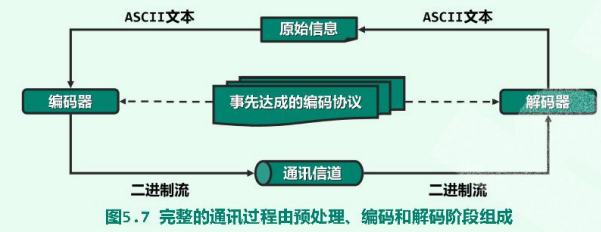

如上图所示，编码 和 解码 的任务分别由 发送方和接收方独立完成。故在开始通讯之前，双方已经以某种形式，就编码规则达成过共同的协议（通过编码表的制定，建立起协议）。

编码表
原始信息的基本组成单位称为“字符”，它们都有来自某一特定的有限集合，也成为 字符集（alphabet）。

以二进制形式承载的信息，都可以表示为来自编码表![](https://cdn.nlark.com/yuque/__latex/d9eb6f5379b97dfdb84fb1e6372e7c0f.svg#card=math&code=%E3%80%8C&height=24&width=16)={0, 1}*的某一特定二进制串。从这个角度理解，每一编码表都是从字符集 到编码表 的一个单射，

• 编码就是对信息文本中各字符逐个实施这一映射的过程；
• 解码则是逆向映射的过程。

编码表实例

二进制编码
所谓编码，就是对于任意给定的文本，通过查阅编码表逐一将其中的字符转译为二进制编码。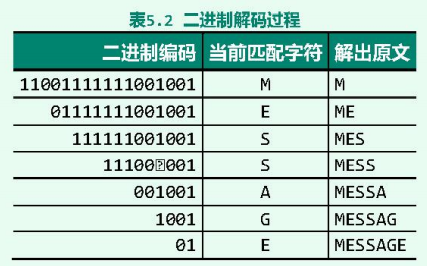

制编码，这些编码依次串接起来即得到了全文的编码。比如若待编码文本为”MESSAGE”，则根据由表5.1确定的编码方案，对应的二进制编码串应为：。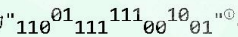

二进制解码
由编码器生成的二进制流经过 信道 送达之后，接收方可以按照事先约定的 编码表（表5.1），依次扫描各比特位，并经匹配逐一转译出个字符，从而最终恢复出原始的文本。

解码歧义
虽然，编码表确定之后，编码 的结果是确定的；但是 解码 过程却不见得唯一。
如：

可以看出，与表5.1差异在于：字符“M”的编码变为“11”。此时，解码方法就会变的至少有两种：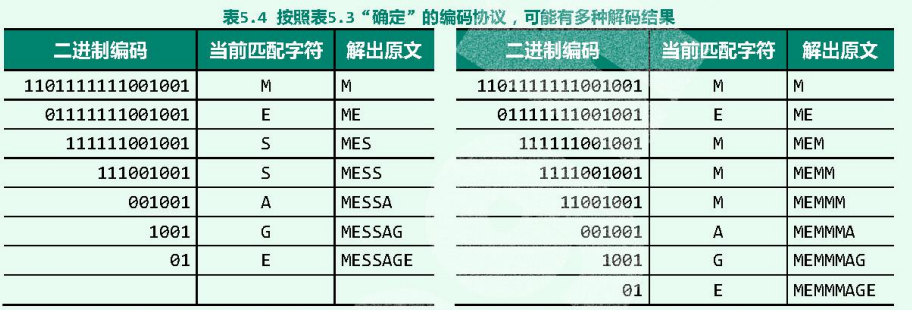

前缀无歧义编码
由上述可知，若编码表制定不当，就可能会使解码过程出现歧义甚至是错误。
所以，为了消除 解码时的歧义，任何两个原始字符所对应的的二进制编码串，互相都不是前缀。

如，在表5.3中，字符“M”的编码（“11”）即为字符“S”的编码（“111”）的前缀，于是编码串“111111”既可以解释为： 也可以解释为：

所以，只要各字符的编码互不为前缀，则即便出现无法解码的错误，也不可能出现歧义。
这类编码方案就是“前缀无歧义编码”（prefix-free code），简称：PFC编码。

5.2 二叉编码树

任一编码方案都可以描述为一颗二叉树：

• 从根节点出发，每次向左(右)对应一个0(1)比特位。各字符分别存放于对应的叶子中。字符x 的编码串rps(v(x))=rps(x) 由 根 到 v(x) 的通路确定。

  由 从根节点 到 每一个 字符所在节点 的唯一通路， 可以为各节点v赋予一个互异的二进制串，称作 根通路串（root path string），记作rps(v) 。

PFC编码树
字符编码不必等长，所有字符都对应于叶节点，不存在解码歧义现象，为前缀无歧义编码，不同字符的编码互不为前缀，故不致歧义，此为可行的PFC编码方案。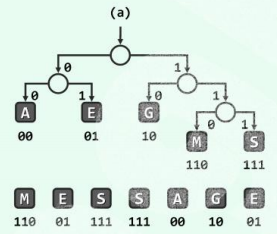

PFC编码树

基于PFC编码树的解码
得到PFC编码串之后，对比PFC的编码树：

从根节点出发，根据编码串的当前编码相应地向左(比特0)或向右(比特1)深入，一旦抵达叶节点，则输出其对应的字符，并随即复位至根节点。

将整个编码串完成解码后，就可以解码得出字符串。

实际上，这一解码过程甚至可以在二进制编码串的接受过程中实时进行，而不必等到所有比特位都到达之后才开始进行，因此这类算法属于在线算法。

可见，算法无法继续的唯一可能情况为：在准备向下深入时没有发现对应的分支，然而根据定义和约束条件，PFC编码树必然是真二叉树，每一内部节点必然拥有左、右分支，因此上述情况不可能发生。

5.2.1 最优编码树

在实际的通讯系统中，信道的使用效率很大程度上取决于编码本身的效率。比如，高效的算法生成的编码串应尽可能短。

字符x的编码长度|rps(x)|为其对应叶节点的深度depth(v(x))。于是，各字符的平均编码长度就是编码树T中的叶节点平均深度。


平均编码长度是反应编码效率的重要指标，我们尽可能希望这一指标小。同一字符集的所有编码方案中，平均编码长度最小者被称为最优方案，对应编码树的ald()值达到最小，故称之为最优编码树，简称最优编码树**。对于任一字符集，最优编码树必然存在。

不唯一性
最优编码树 不一定唯一**（比如，同层节点互换位置，并不影响全树的平均深度）。

双子性
最优编码树 必然为 真二叉树**，内部节点的左、右孩子全双。
不然，假设其中内部节点p有唯一的孩子x，则将p删除并代之以子树x。除了子树中所有叶节点的编码长度统一缩短一层外，其余叶节点的编码长度不变，相比于之前的编码树平均编码长度必然更短。这与最优性矛盾。

层次性
叶节点位置深度之差不超过1，类似双子性的证明，替换后可得到的编码树平均编码长度更短，不符合最优编码树的原则。

最优编码树的构造
真完全树为最优编码树，可直接导出构造最优编码树的算法：
创建一颗规模为的完全二叉树T，再将中的字符任意分配给T的个叶节点。

比如，仍以字符集E = {‘A’, ‘E’,‘G’，’M’，’S’}为例，只需创建包含2x5- 1=9 个节点的一棵完全二叉树，并将各字符分配至5个叶节点，即得到一-棵最优编码树。再适当交换 同深度的节点，即可得到如116页图5.9(a)所示的编码树由 于此类节点交换并不改变平均编 码长度，故它仍是一棵最优编码树。

5.2.2 Huffman编码树

以上最优编码树算法中的平均编码长度的策略在实际应用中价值并不大， 除非中各字符在文本传中出现的次数相同。但是这一条件往往不满足，甚至不确定。

所以，需要从待编码的文本串中取出若干样本，通过统计各字符在其中出现的次数(也称作：字符的频率），估计各字符实际出现的概率。但是实际情况下，字符集中各字符出现频率极少相近的，往往相差悬殊。所以，需要从 带权平均编码长度 出发。

若考虑字符各自出现频率，则可将带权平均编码长度取作编码树T的叶节点带权平均深度，即是：

完全二叉编码树wald() 最短

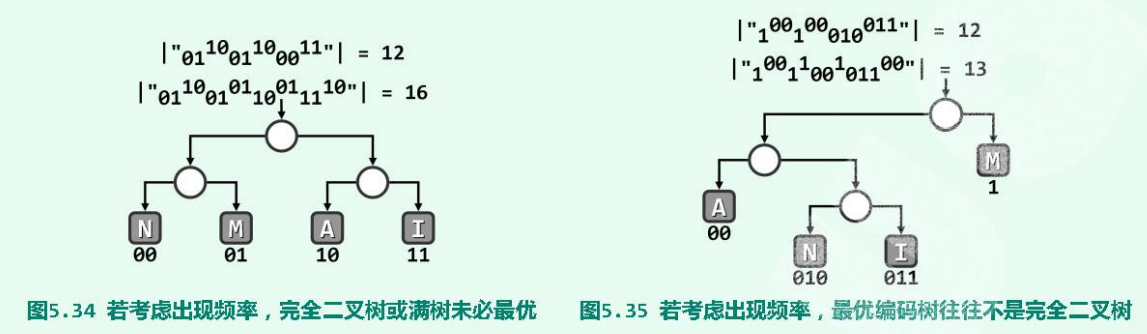
以为例，求字符串“MAMMAMIA”的 带权平均编码长度

计算结果：在完全二叉编码树中，wald(T)为2；在第二种情况的编码树中，wald(T)为1.625。更小。

所以，完全二叉编码树wald() 最短


**

5.2.2.1 最优带权编码树⭐⭐

最优编码树 不一定是 完全二叉编码树。

频率高的超字符，应尽可能放在离根节点 较近的位置。

同样，huffman编码树满足层次性、双子性、不唯一性。

5.2.2.2 Huffman编码算法

对于字符出现概率已知的任一字符集，都可以采用如下算法构造对应的 最优带权编码树：

• 首先，对应于字符集的每一个字符，分别建立一棵单个节点的树，其权重取作该字符的频率，这棵树构成一个森林**S**。

**

• 然后，从森林S 中选取**权重最小**的两棵树，创建一个新节点，并分别以这两棵树作为其左、右孩子，如此，它们合并为一个更高的树，新树的权重为 二者权重之和。（可以将合并后的新树等效的视作一个字符，为 超字符。）

• 重复第二步，不断地进行合并，每经一次合并，森林S 中的树就减少一棵，当森林S中的树只有一棵树时，就是那个 最优带权编码树，至此构造完成。

上述构造过程称为：Huffman编码算法。

由其生成的编码树称作Huffman编码树。最带权优编码树 可以有不止一棵，所以Huffman编码树 只是 最带权优编码树 中的一棵。

5.2.3 Huffman编码树 代码部分

5.2.3.1 相关数据的结构：

具体代码部分：可在https://github.com/longlongqin/DataStructure/tree/master/DSACPP/BinTree中查看，或者参考教材。

1. 超字符

如前所述，无论是输入的字符还是合并后得到的超字符，在构造Huffman编码树过程中，都可等效处理——究其本质，相关信息无非就是对应字符及其出现频率。

1. Huffman编码树

可借助BinTree模板类 定义Huffman编码树类型：HuffTree。

//Huffman编码树（由BinTree派生，节点类型为HuffChar）
#define HuffTree    BinTree<HuffChar>

1. Huffman森林

借助List模板类定义Huffman森林类型HuffForest。

//Huffman森林（使用List模板类实现）
typedef List<HuffTree*> HuffForest; //Huffman森林

1. Huffman二进制编码串

借助位图Bitmap（习题【2-34】）定义Huffman二进制编码串类型huffCode。

//Huffman二进制编码
#include "Bitmap.h" //基于Bitmap实现
typedef Bitmap Huffman;

对于位图的实现中相关的“位运算”值得学习。传送门

1. Huffman编码表

借助散列表来实现。

//Huffman编码表（留个坑这里使用HashTable实现，待到那时再补全HashTable的实现⭐⭐）
#include "../HashTable/HashTable.h" //用HashTable实现（记得回来补全它）
typedef HashTable<char, char*> HuffTable; //Huffman编码表

现在还没学到散列表，到时候还需要回来补全一下子。

5.2.3.2 构造Huffman编码树

HuffTree* minHChar ( HuffForest* forest ) { //在Huffman森林中找出权重最小的（超）字符
   ListNodePosi ( HuffTree* ) p = forest->first(); //从首节点出发查找
   ListNodePosi ( HuffTree* ) minChar = p; //最小Huffman树所在的节点位置
   int minWeight = p->data->root()->data.weight; //目前的最小权重
   while ( forest->valid ( p = p->succ ) ) //遍历所有节点
      if ( minWeight > p->data->root()->data.weight ) //若当前节点所含树更小，则
         {  minWeight = p->data->root()->data.weight; minChar = p;  } //更新记录
   return forest->remove ( minChar ); //将挑选出的Huffman树从森林中摘除，并返回
}
HuffTree* generateTree ( HuffForest* forest ) { //Huffman编码算法
   while ( 1 < forest->size() ) {
      HuffTree* T1 = minHChar ( forest ); HuffTree* T2 = minHChar ( forest );
      HuffTree* S = new HuffTree(); 
      S->insertAsRoot ( HuffChar ( '^', T1->root()->data.weight + T2->root()->data.weight ) );
      S->attachAsLC ( S->root(), T1 ); S->attachAsRC ( S->root(), T2 );
      forest->insertAsLast ( S ); 
   } //assert: 循环结束时，森林中唯一（列表首节点中）的那棵树即Huffman编码树
   return forest->first()->data;
}

也就是：

• 在Huffman森林中迭代的找出当前最小的两个（超）字符 T1，T2；
• 将这两个（超）字符组合成一个新的超字符（新的树），并将新树并入Huffman森林中，同时将T1，T2从Huffman森林中删除；
• 直到Huffman森林中之剩下一棵树，则这棵树就是所求的Huffman编码树

每迭代一次，森林的规模减1,故共需迭代n-1此，直到只剩一棵树。minHChar() 每次都要遍历森林中所有的超字符，所需时间线性正比于当时森林的规模。因此总体运行时间应为：

5.2.3.3 生成Huffman编码表

//通过遍历获取各字符的编码
static void generateCT ( Bitmap* code, int length, HuffTable* table, BinNodePosi ( HuffChar ) v ) {
   if ( IsLeaf ( *v ) ) //若是叶节点（还有多种方法可以判断）
      {  table->put ( v->data.ch, code->bits2string ( length ) ); return;  }
   if ( HasLChild ( *v ) ) //Left = 0 向左走向为0
      { code->clear ( length ); generateCT ( code, length + 1, table, v->lc ); }
   if ( HasRChild ( *v ) ) //Right = 1 向右走向为1
      { code->set ( length ); generateCT ( code, length + 1, table, v->rc ); }
}
HuffTable* generateTable ( HuffTree* tree ) { //将各字符编码统一存入以散列表实现的编码表中
   HuffTable* table = new HuffTable; Bitmap* code = new Bitmap;
   generateCT ( code, 0, table, tree->root() ); release ( code ); return table;
};

注意在获取字符的编码中，可以看到“Left = 0，Right = 1”的注释。这个其实是一种规定，向左孩子走的通路编码为0，向右孩子的通路的编码为1。如下图所示： 向左孩子走的通路编码为0，向右孩子的通路的编码为1

5.2.3.4 编码、解码

这里的编码、解码部分代码，暂时还不太理解。

//    编码
int encode ( HuffTable* table, Bitmap* codeString, char* s ) { //按照编码表对Bitmap串编码
   int n = 0; //待返回的编码串总长n
   for ( size_t m = strlen ( s ), i = 0; i < m; i++ ) { //对于明文中的每个字符
      char** pCharCode = table->get ( s[i] ); //取出其对应的编码串
      if ( !pCharCode ) pCharCode = table->get ( s[i] + 'A' - 'a' ); //小写字母转为大写
      if ( !pCharCode ) pCharCode = table->get ( ' ' ); //无法识别的字符统一视作空格
      printf ( "%s", *pCharCode ); //输出当前字符的编码
      for ( size_t m = strlen ( *pCharCode ), j = 0; j < m; j++ ) //将当前字符的编码接入编码串
         '1' == * ( *pCharCode + j ) ? codeString->set ( n++ ) : codeString->clear ( n++ );
   }
   printf ( "\n" ); return n;
} //二进制编码串记录于位图codeString中

//        解码
// 根据编码树对长为n的Bitmap串做Huffman解码
void decode ( HuffTree* tree, Bitmap* code, int n ) {
   BinNodePosi ( HuffChar ) x = tree->root();
   for ( int i = 0; i < n; i++ ) {
      x = code->test ( i ) ? x->rc : x->lc;
      if ( IsLeaf ( *x ) ) {  printf ( "%c", x->data.ch ); x = tree->root();  }
   }
   /*DSA*/if ( x != tree->root() ) printf ( "..." ); printf ( "\n" );
} //解出的明码，在此直接打印输出；实用中可改为根据需要返回上层调用者

5.2.4 小结

Huffman编码树的构造：

• 需要：Huffman森林（主要信息就是 字符 及 该字符出现的频率）

步骤：

• 首先，将待处理的字符串中各字符的出现频率求出来；
• 将每个字符串中的每个字符都处理成一颗树，此时就生成了Huffman森林；

• 根据Huffman森林，求出Huffman编码树。（具体步骤如下）

  • 迭代的找出当前最小的两个（超）字符 T1，T2；
  • 将这两个（超）字符组合成一个新的超字符（新的树），并将新树并入Huffman森林中，同时将T1，T2从Huffman森林中删除；
  • 直到Huffman森林中之剩下一棵树，则这棵树就是所求的Huffman编码树

• 然后，根据求得的编码树，生成Huffman编码表。

• 最后，就可以根据Huffman编码表，进行编码、解码 操作。（编码表就是 编码、解码 时 遵守的一种协议）。