在计算机科学里，k-d树（ k-维树)（k-dimensional tree）的缩写）是在k维欧几里德空间组织点的数据结构。k-d树可以使用在多种应用场合，如多维键值搜索（例：范围搜寻及最邻近搜索）。k-d树是空间二分树（Binary space partitioning）的一种特殊情况。

1 简介

k-d树是每个叶子节点都为k维点的二叉树。所有非叶子节点可以视作用一个超平面把空间分割成两个半空间。节点左边的子树代表在超平面左边的点，节点右边的子树代表在超平面右边的点。

选择超平面的方法如下：每个节点都与k维中垂直于超平面的那一维有关。因此，如果选择按照x轴划分，所有x值小于指定值的节点都会出现在左子树，所有x值大于指定值的节点都会出现在右子树。这样，超平面可以用该x值来确定，其法线为x轴的单位向量。

2 kd树的创建

有很多种方法可以选择轴垂直分割面（ axis-aligned splitting planes ），所以有很多种创建k-d树的方法。 最典型的方法如下：

• 随着树的深度轮流选择轴当作分割面。（例如：在三维空间中根节点是 x 轴垂直分割面，其子节点皆为 y 轴垂直分割面，其孙节点皆为 z 轴垂直分割面，其曾孙节点则皆为 x 轴垂直分割面，依此类推。）
• 点由垂直分割面之轴座标的中位数区分并放入子树。

这个方法产生一个平衡的k-d树。每个叶节点的高度都十分接近。然而，平衡的树不一定对每个应用都是最佳的。

为了方便理解，我们举一个k = 2时的例子。（参考：https://zhuanlan.zhihu.com/p/23966698）

首先随机在 中随机生成 13 个点作为我们的数据集。

1、首先先沿 x 坐标进行切分，我们选出 x 坐标的中位点，获取最根部节点的坐标：

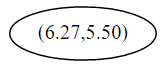
并且按照该点的x坐标将空间进行切分，所有 x 坐标小于 6.27 的数据用于构建左枝，x坐标大于 6.27 的点用于构建右枝。

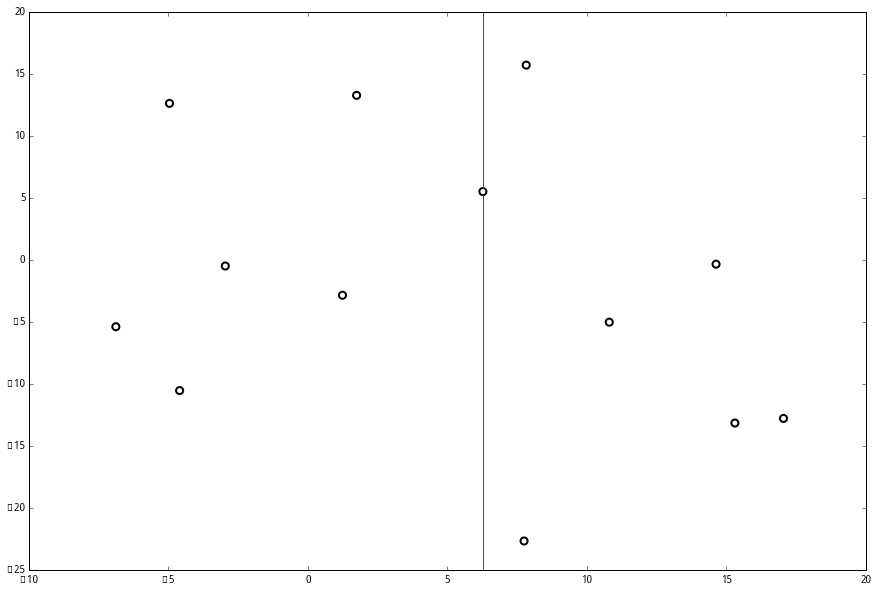
2、下一步，第二维（本例中指y轴）。 对应 y 轴，左右两边再按照 y 轴的排序进行切分，中位点记载于左右枝的节点。得到下面的树，左边的 x 是指这该层的节点都是沿 x 轴进行分割的。

空间的切分如下：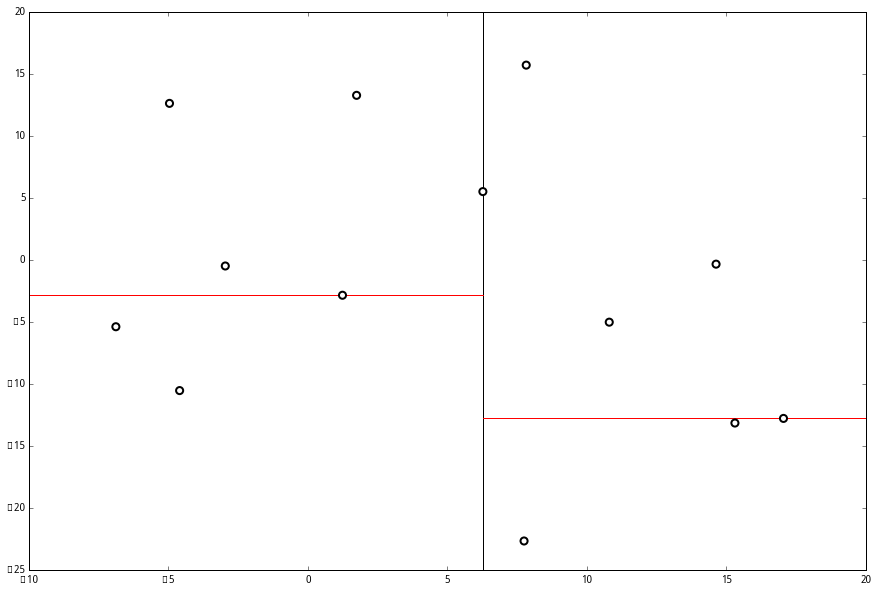

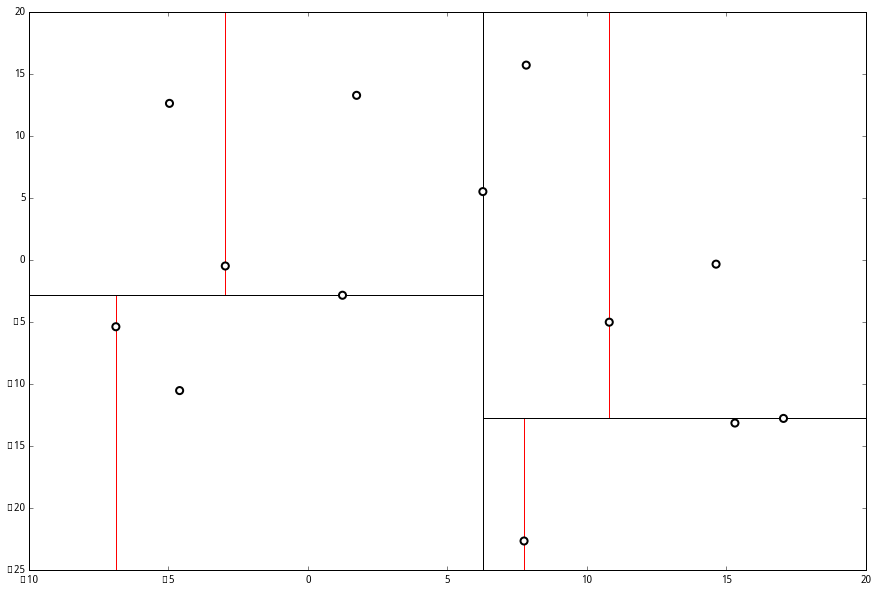
3、轮流循环的对不同维度进行切分。现在又轮到x轴。对应 x 轴，所以下面再按照 x 坐标进行排序和切分，有：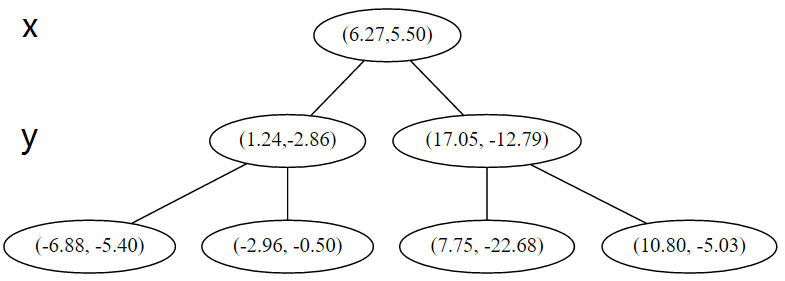


4、最后，每一部分都只剩一个点，将他们记在最底部的节点中。因为不再有未被记录的点，所以不再进行切分。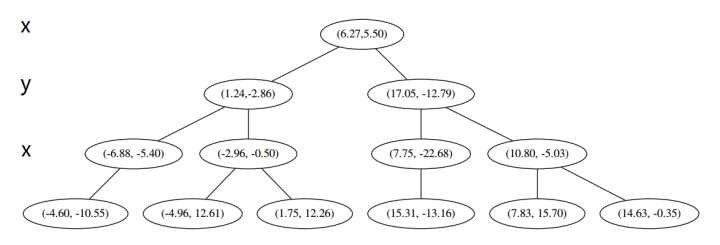


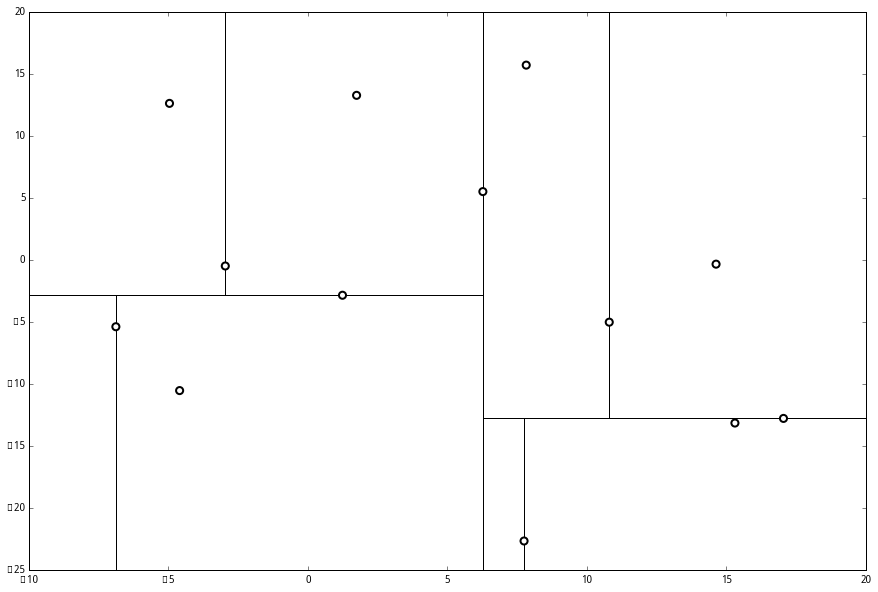
至此，完成了 kd 树的构造。