在已经有了AVL之类的BBST，为什么还需要引入红黑树？

答：我们希望数据结构具有关联性，即相邻版本之间，比如说第一次插入，和第二次插入时，树的结构不能发生太大变化，应该可以经过O(1)次数就可以变化完成。

  • 对于AVL树来说，插入是满足这个条件的，删除却不满足这个条件。
  • 红黑树就满足这一特性，插入和删除操作后的拓扑变化不会超过O(1)。红黑树通过为节点指定颜色，并巧妙地动态调整，可在每次插入或删除之后仅需常数个节点。尽管最坏情况下需对Ω(logn)个节点重染色，但是分摊意义而言仅为O(1)个。

与之前类似，便于分析，红黑树同样引入外部节点。

引入外部节点的数目为：n+1，证明： image.png


1 红黑树的定义与名词

1.1 定义

前提：给红黑树添加外部节点，保证为真二叉树

  1. 树根：必为黑色，即帽子是黑色
  2. 外部节点：必为黑色，即靴子为黑色
  3. 其余节点：若为红节点，则只能有黑色孩子
    • 红之子、之父必须为黑色
  4. 外部节点到根：途中黑节点数目相等
    • 所有外部节点到根经过的黑色节点数目相同，用来控制平衡

实际上，红节点 的孩子、父亲 只能是 黑色的。

概括来说：

  • 树根：一定为黑色；
  • 内部节点（除去树根的内部节点）：可以是黑色、或者红色（但当为红色时，其父与子必为黑色）；
  • 外部节点：一定为黑色；
  • 最后是控制平衡：所有外部节点到根经过的黑色节点数目相同。

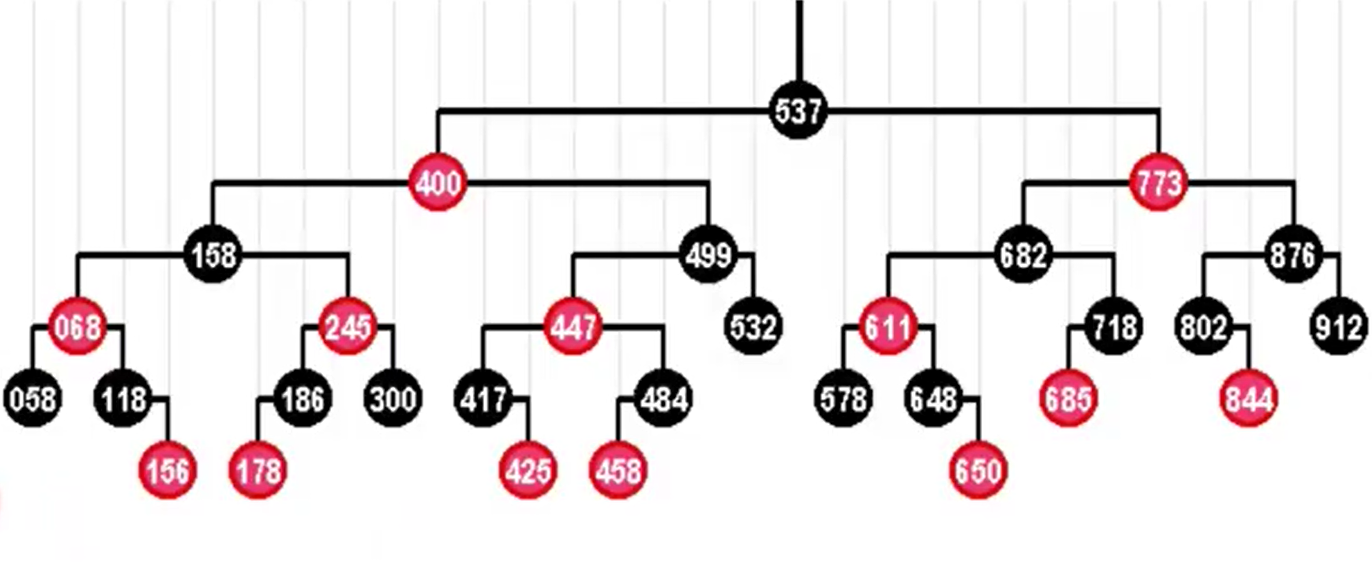
image.png
注意，上图的外部节点没有显式的画出来

1.2 名词

黑深度(black depth)：除去根节点，沿途所经黑节点的总数称作该节点的 黑深度。

根节点的黑深度为0，其余以此类推。

黑高度(black height)：除去(黑色)外部节点，沿途所经黑节点的总数称作该节点的 黑高度。

所有外部节点的黑高度为0，其余以此类推。

2 提升变换

由于红黑树的定义不直观。但是我们可以借助之前已经学习过的数据结构“B-树”。红黑树与 B-树 之间存在一定的联系。

具体地提升变换操作：

  • 首先，将红节点提升至与其（黑）父亲等高——于是每棵红黑树，都对应于一棵(2,4)-树
  • 然后，将黑节点与其红孩子（们）视作关键码，并合并为B-树的超级节点…

从而，可知 无非四种组合，分别对应于4阶B-树的一类内部节点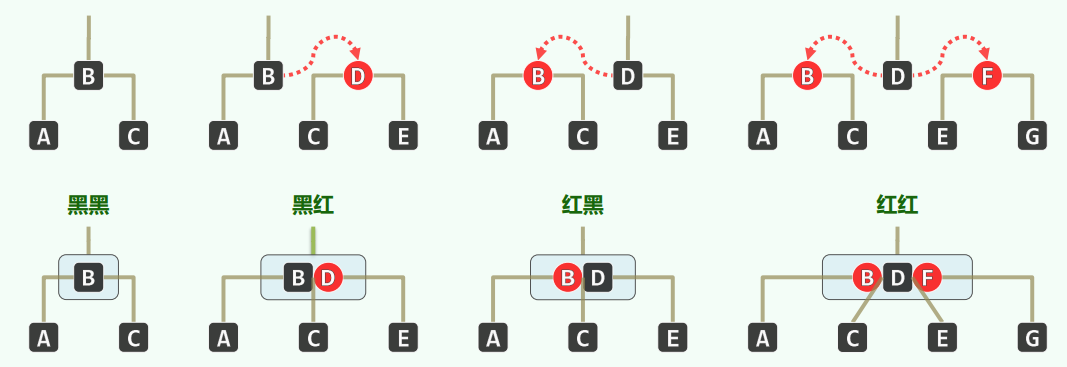
image.png

2.1 红黑树，即是 B-树【(2,4)树】

通过提升变换之后，红黑树即可变为(2,4)树。

3 平衡性

包含n个内部节点的红黑树T，高度为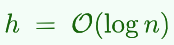image.png //既然B-树是平衡的，由等价性红黑树也应是

更严格的有：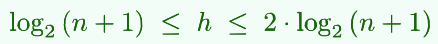
image.png

  • 对于不等式的左半边可以比较容易的出结果；
  • 对于不等式的右半边：

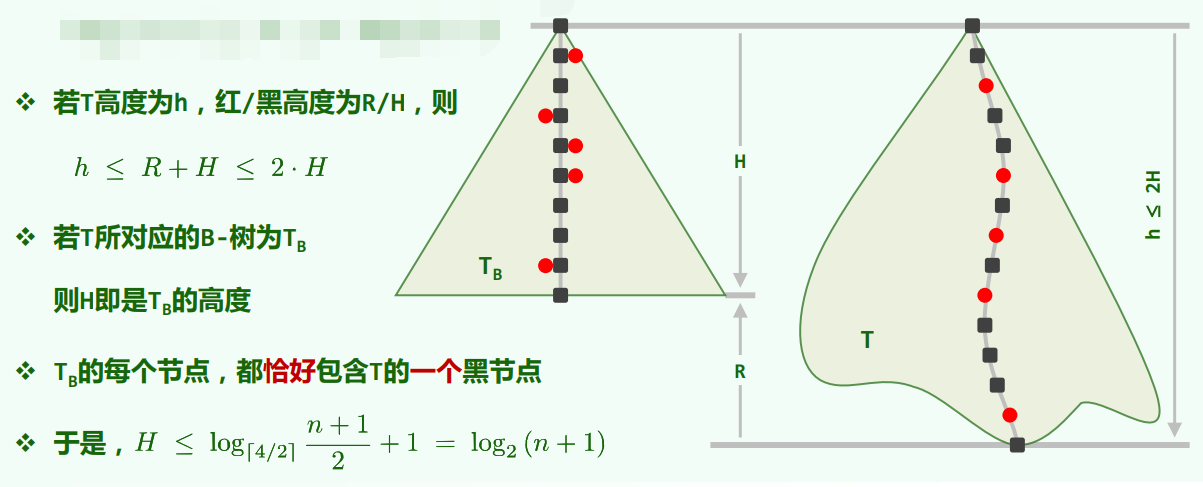
image.png
上图中，最后一行是由公式：https://www.yuque.com/longlongqin/xkqqbk/ycova0#tDPxs 得到的。

也就是说，尽管红黑树不能如完全树那样可做到理想平衡，也不如AVL树那样可做到较严格的适度平衡，但其高度仍控制在最小高度的两倍以内（习题[8-11]），从渐进的角度看仍是o(logn)，依然保证了适度平衡——这正是红黑树可高效率支持各种操作的基础。

4 插入

按照BST规则插入关键码e

不妨假定经调用接口search()查找之后，确认目标节点尚不存在。在查找失败处的位置x创建节点，并随即将其染成红色(除非此时全树仅含一个节点)。

  • 首先，使用search()函数查找插入位置。（插入位置必为末端节点）
  • 然后，在查找失败处的位置x处创建节点，并将新创建的节点染成红色；
  • 随后，进行检查是否出现双红缺陷，如果出现则进行解决。【对照红黑树定义的4个条件，只有（3）未必满足，即，此时x的父亲可能也是红色，从而出现 双红缺陷】
  • 最后，双红缺陷(如果有)修正后，则返回插入的位置。 ```cpp BinNodePosi RedBlack::insert(const T& e) { BinNodePosi& x = search(e); if (x) return x; //如果，在原黑红树中找到了关键码e的节点，则立即返回 x = new BinNode(e, hot, nullptr, nullptr, -1); //否则（原树中不存在关键码e），创建红节点x，以hot为父，黑高度为-1 solveDoubleRed(x); //经双红修正后，即可返回 return x ? x : hot->parent; } //无论e是否存在原树中，返回时总有 x->data_ == e
  1. <a name="O36sd"></a>
  2. ## 4.1 双红缺陷 及 修正
  3. **因新节点的引入，而导致父子节点同为红色的此类情况，称作“双红”(double red）。**为修正双红缺陷，可调用`solveDoubleRed(x)`接口。每引入一个关键码，该接口都可能迭代地调用多次。在此过程中，当前节点`x`的兄弟及两个孩子（初始时都是外部节点），始终均为黑色。
  5. 将`x`的父亲与祖父分别记作`p`和`g`。既然此前的红黑树合法，故作为红节点p的父亲，g必然存在且为黑色。g作为内部节点，其另一孩子（即p的兄弟、x的叔父）也必然存在，将其记作`u`。以下，视节点u的颜色不同，分两类情况分别处置。
  7. - **`x`**：插入的节点；
  8. - `**p**`：x的父亲；【当出现双红时，p是红色】
  9. - **`g`**：x的祖父；【必为 黑色】
  10. - **`u`**：x的叔父；
  12. 下面将根据x的叔父u的颜色，分两种情况讨论：
  13. <a name="w2ZHM"></a>
  14. ### 4.1.1 双红修正（RR-1）：叔父节点u为黑色
  15. 首先，考查u为黑色的情况。**此时，x的兄弟、两个孩子的黑高度，均与u相等**。图8.25(a)和(b)即为此类情况的两种可能（另有两种对称情况，请读者独立补充）。<br />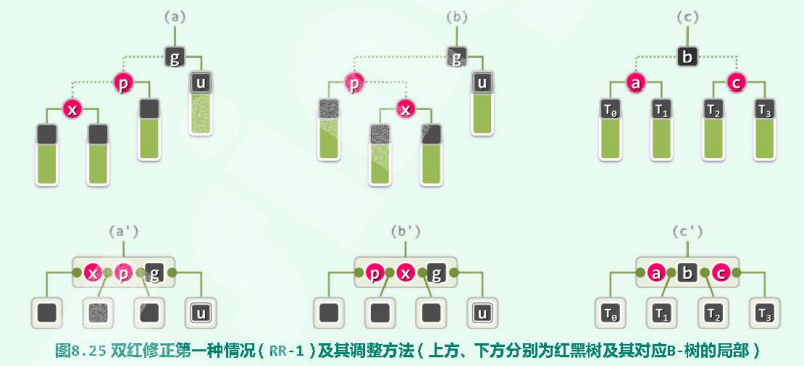![image.png](https://cdn.nlark.com/yuque/0/2020/png/1282860/1600009977952-f9151c60-72cd-415f-a984-a5b39ff6cb40.png#align=left&display=inline&height=366&margin=%5Bobject%20Object%5D&name=image.png&originHeight=366&originWidth=804&size=279730&status=done&style=stroke&width=804)<br />此时红黑树条件(3)的违反：
  17. - 首先，**从B-树角度等效地看**，即同一节点不应包含紧邻的红色关键码。故如图8.25(`c'`)所示，**只需令黑色关键码与紧邻的红色关键码****互换颜色**。
  18. - 然后，**从图(`c`)红黑树的角度看**，这等效于按中序遍历次序**，对节点x、p和g及其四棵子树，做一次****局部“3＋4”重构**。
  20. 调整之后，局部子树的黑高度将复原，全树的平衡必然得以恢复。同时，新子树的根节点为黑色，也不致于引发新的双红现象。至此，整个插入操作遂告完成。
  22. 具体操作过程就是：
  23. > 这种情况，各节点的颜色：
  24. > - x红色；
  25. > - p红色；
  26. > - g黑色；
  27. > - u黑色；
  29. - 首先**染色**，查看x与p的位置：
  30.    - 当x与p同一侧时（zig-zig或者zag-zag），则p由红变黑（其实是与g（黑色）交换颜色），x保持红色不变；
  31.    - 当x与p异侧（zig-zag或者zag-zig）时，则x由红变黑（其实是与g（黑色）交换颜色），p保持红色不变；
  32. - 然后**旋转**，使用`rotateAt()`函数；
  33. - 最后将“3+4”调整后的子树的跟节点 与 原子树的曾祖父(g的父亲) 进行连接。
  35. <a name="7hXL7"></a>
  36. ### 4.1.2 双红修正（RR-2）：叔父节点u为红色
  37. 再考查节点u为红色的情况。**此时，u的左、右孩子非空且均为黑色，其黑高度必与x的兄弟以及两个孩子相等**。图8.26(a)和(b)给出了两种可能的此类情况（另两种对称情况，请读者独立补充）。<br />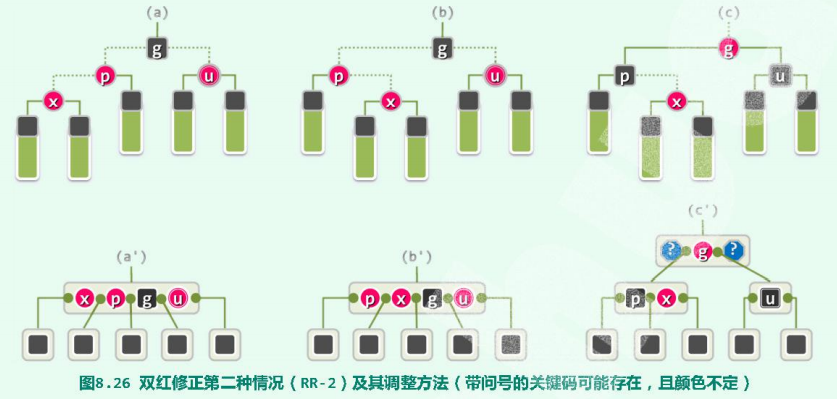![image.png](https://cdn.nlark.com/yuque/0/2020/png/1282860/1600010217491-a4b4cedb-6989-4f6b-b932-2fdcd88c24d2.png#align=left&display=inline&height=399&margin=%5Bobject%20Object%5D&name=image.png&originHeight=399&originWidth=837&size=332746&status=done&style=stroke&width=837)<br />此时红黑树条件(3)的违反，从B-树角度等效地看，即该节点因超过4度而发生上溢。
  39. - 首先，以图8.26(b)为例。**从图(c)红黑树的角度来看**，只需将红节点p和u转为黑色，黑节点g转为红色，x保持红色。**
  40. - 然后，**从图(`c'`)B-树的角度**来看，等效于上溢节点的一次分裂。不难验证，如此调整之后局部子树的黑高度复原。**然而，子树根节点g转为红色之后，有可能在更高层再次引发双红现象**。对应于在关键码g被移出并归入上层节点之后，进而导致上层节点的上溢-----即上溢的向上传播。
  41.    - 等效地将g视为刚插入的节点，**分以上两类情况如法处置**。每经过这样一次迭代，节点g都将在B树中上升一层，而在红黑树中存在双红缺陷的位置也将相应地上升两层，故累计至多迭代`O(logn)`次。
  45. 若最后一步迭代导致树根的分裂，并由g独立地构成新的树根节点，则应强行转为黑色，如此，全树的黑高度随即增加一层。
  47. 具体操作过程就是：
  49. - `P`与`U`由红色变为黑色；当`g`不是根节点时，由黑色变为红色；
  50. - 然后，从B-树的角度来看，发生了节点的上溢，所以，**需要等效地将g视为刚插入的节点**，重回起点（又一次递归（即，又调用一次`solveDoubleRed`函数））：
  51.    - u为黑色时，..........
  52.    - u为红色时，..........
  54. 直到，递归至树根节点，结束。
  55. <a name="3sng8"></a>
  56. ### 4.1.3 双红修正的代码
  57. ```cpp
  58. /******************************************************************************************
  59.  * RedBlack双红调整算法：解决节点x与其父均为红色的问题。分为两大类情况：
  60.  *    RR-1：2次颜色翻转，2次黑高度更新，1~2次旋转，不再递归
  61.  *    RR-2：3次颜色翻转，3次黑高度更新，0次旋转，需要递归
  62.  ******************************************************************************************/
  63. template<typename T>
  64. void RedBlack<T>::solveDoubleRed(BinNodePosi<T> x)
  65. {
  66.     if (IsRoot(*x)) // 如果已经（递归）至树根，则将其转黑色，更新树高
  67.     {
  68.         root_->color_ = RB_BLACK;
  69.         root_->height_++;
  70.         return;
  71.     }
  72.     // 否则，x的父亲必然存在
  73.     BinNodePosi<T> p = x->parent_; if (IsBlack(p))    return; //当p为黑色时，就无需在调整，因为没有出现“双红缺陷”
  75.     BinNodePosi<T> g = p->parent_; //当p为红，则出现“双红缺陷”，此时x的祖父g必然存在，且g必为黑色
  76.     BinNodePosi<T> u = uncle(x); //以下，根据x的叔父u的颜色分情况讨论：
  78.     if (IsBlack(u)) //1. u为黑色(含null)时
  79.     {
  80.         if (IsLChild(*x) && IsLChild(*p)) //当x与p同一侧时（zig-zig或者zag-zag），则
  81.             p->color_ = RB_BLACK; //p由红变黑，x保持红色不变
  82.         else //当x与p异侧（zig-zag或者zag-zig）时，则
  83.             x->color_ = RB_BLACK; //x由红变黑，p保持红色不变
  84.         g->color_ = RB_RED; //g一定由黑变红，因为无论x与p的位置如何，他们做的都是与g交换颜色
  86.         BinNodePosi<T> gg = g->parent_; //曾祖父
  87.         BinNodePosi<T> r = FromParentTo(*g) = rotateAt(x); //“3+4”调整后的子树根节点
  88.         r->parent_ = gg; //与原曾祖父连接
  89.     }
  90.     else //2. u为红色时
  91.     {
  92.         p->color_ = RB_BLACK; p->height_++; //p由红变黑（所以，高度+1）
  93.         u->color_ = RB_BLACK; u->height_++; //u由红变黑（所以，高度+1）
  94.         if (!IsRoot(*g)) g->color_ = RB_RED; //g非根节点，才可以将其转为红色
  95.         solveDoubleRed(g); //等效地将g视为刚插入的节点（类似于尾递归，可优化为迭代形式）
  96.     }
  97. }

4.1.4 双红修正的复杂度

以上情况的处理流程可归纳为图8.27。其中的重构、染色等局部操作均只需常数时间，故只需统计这些操作在修正过程中被调用的总次数。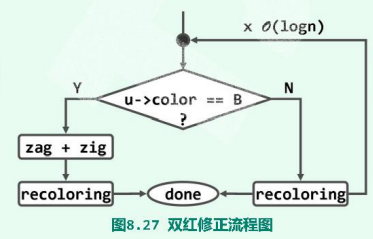
image.png

具体统计，可归纳为表8.1。可见，

  • 对于前一种情况，只需做一轮修正；
  • 后一种情况虽有可能需要反复修正，但由于修正位置的高度会严格单调上升，故总共也不过O**(**logn)轮。

另外从下表也可看出，每一轮修正只涉及到常数次的节点旋转或染色操作。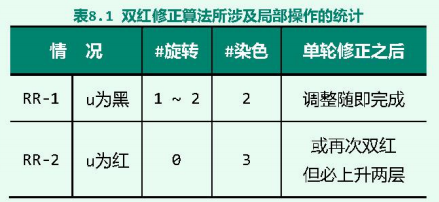
image.png

5 删除

5.1 算法流程

按照BST规则删除关键码e

  • 首先，首先调用 BST::search(e)进行查找，若查找成功，则调用内部接口removeAt(x)删除。

    按照removeAt(x)函数的定义，x为实际被删除者，其父亲为p = hot_，其接替者为r，而r的兄弟为外部节点w = NULL （因为w是假设的节点，所直接设置为NULL，也就满足“随其父亲x一并被摘除”）。

  • 然后，要讨论删除的这个节点的位置：

      1. 删除节点位于树根：则无论r颜色如何，只需将其置为黑色并更新黑高度即可。
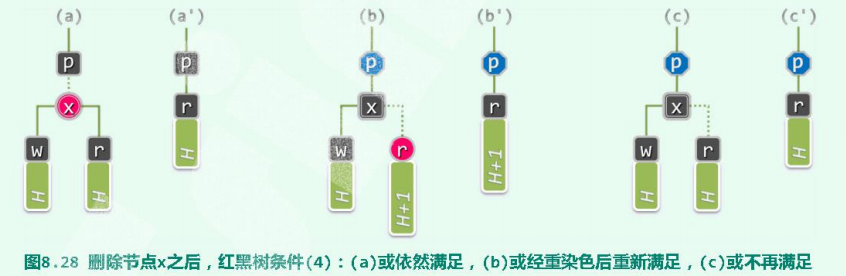
      1. 删除的节点不在树根，因随后的复衡调整位置可能逐层上升，故不妨等效地理解为：w是与r黑高度相等的子红黑树，且随其父亲x一并被摘除。如此，可将**x**统一视作双分支节点，从而更为通用地描述以下算法。【不难验证，此时红黑树的前两个条件继续满足，但后两个条件却未必。因此不妨假定，x**的父亲p存在**。】
        • 2.1 若如图8.28(a)所示x为红色，则在摘除子树w，并将x替换为r之后，如图(a’)所示局部子树的黑高度即可复原。
        • 2.2 当x**为黑色，只要如图(b)所示`r`为红色**，则如图(b’)所示，只需在删除操作之后将r翻转为黑色，亦可使得局部子树的黑高度复原。
        • 2.3 x为黑色，r为黑色（此时出现，“双黑”）。则在删除操作之后，如图(c’)所示局部子树的黑高度将会降低一个单位。需用函数solveDoubleBlack()来解决双黑问题。

image.png

template<typename T>
bool RedBlack<T>::remove(const T& e)
{
    BinNodePosi<T>& x = search(e); if (!x) return false; //确认目标存在（留意hot_的位置）
    BinNodePosi<T> r = removeAt(x, hot_);    if (!(--size_)) return true; //实施删除

    //assert： hot_的某一孩子被删除，且被r所指节点（可能是NULL）接替。以下检查是否失衡，并做必要检查
    if (!hot_) // 当删除节点位于树根：则无论r颜色如何，只需将其置为黑色并更新黑高度即可。
    {
        root_->color_ = RB_BLACK; 
        updateHeight(root_); 
        return true;
    }
    else // 当删除的节点不在树根，则将x统一视作双分支节点，此时x的父亲p(hot_)存在
    {
        // 2.1 当x为红色时，则在摘除子树w，并将x替换为r之后，即可。
        /* 本来应该使用“if(IsRed(x))”来判断的，这里使用下面的if语句，其实是等价的：
         * 因为，如果x是红色，那就肯定不用更新黑高度。反过来，不用更新黑高度的，说明x一定是红色（因为2.2、2.3是一定会更新的）
         */
        if (BlackHeightUpdated(*hot_)) 
            return true;

        //2.2 当x为黑色，只要如图(b)所示r为红色，则如图(b')所示，
        //只需在删除操作之后将r翻转为黑色，亦可使得局部子树的黑高度复原。
        if (IsRed(r)) //这里之所以不用判断x是黑色，是因为上面的if语句，就是在x为红色时，才执行的。
        {
            r->color_ = RB_BLACK;
            r->height_++;
            return true;
        }

        // 2.3 x为黑色，r为黑色（此时出现，“双黑”）。
        // 此时，需用函数solveDoubleBlack()来解决双黑问题。
        solveDoubleBlack(r);
        return true;
    }
} //若目标节点存在 且被删除，返回true，否则返回false

5.2 双黑及其修正

被删除节点x及其替代者r同为黑色的此类情况，称作“双黑”(double black）。

从B-树的角度来看，当x与r均为黑色，在对应的4阶B-树中，x将单独成为一个超级节点。那么删除x就会引起下溢。

由于，提升变换时，提升的是红节点，而r为黑，s会随着x一起被删除，所以也就相当于，x会单独称为超级节点。

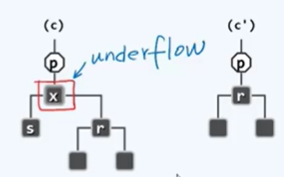
image.png
此时，需调用solveDoubleBlack(r)算法予以修正。为此，需考查两个节点：

  • 原黑节点x的兄弟s (必然存在，但可能是外部节点）；
  • 删除之后，节点r的父亲p。

并视s和p颜色的不同组合，按四种情况分别处置。

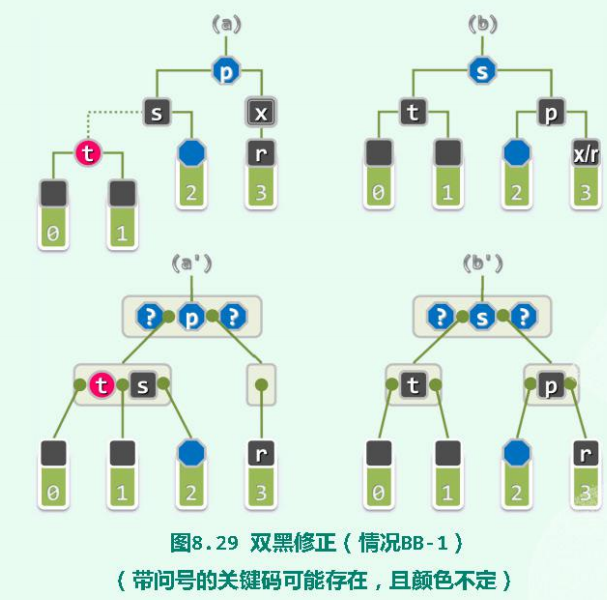
5.2.1 双黑修正（BB-1）：s黑，且s至少有一个红孩子t

image.png

  • 既然节点x的另一孩子w = NULL，故从B-树角度（图8.29(a’)）看节点x被删除之后的情况，可以等效地理解为：关键码x原所属的节点发生下溢；
    • 此时，t和s必然属于B-树的同一节点，且该节点就是下溢节点的兄弟。故可参照B-树的调整方法，下溢节点从父节点借出一个关键码(p)，然后父节点从向下溢节点的兄弟节点借出一个关键码(s），调整后的效果如图(b’)。


  • 从红黑树的角度（图(b)）来看，上述调整过程等效于，对节点t、s和p实施“3＋4”重构。
    • 根据红黑树与B-树的对应关系不难理解，若这三个节点按中序遍历次序重命名为a、b和c，则还需将a和c染成黑色，b则继承p此前的颜色。
    • 就图8.29的具体实例而言，也就是将t和p染成黑色，s继承p此前的颜色。注意，整个过程中节点r保持黑色不变。由图8.29(b)（及其对称情况）不难验证，经以上处理之后，红黑树的所有条件，都在这一局部以及全局得到恢复，故删除操作遂告完成。


5.2.2 双黑修正（BB-2R）：s黑，且两个孩子均为黑；p为红

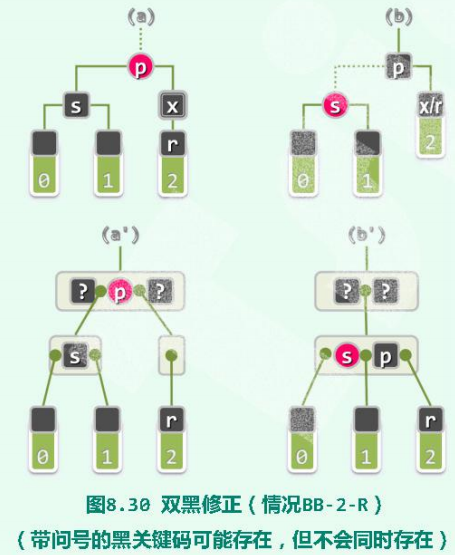
image.png
与BB-1类似，在对应的B-树中，关键码x的删除导致其所属的节点下溢。但因此时关键码s所在节点只有两个分支，故下溢节点无法从父节点借出关键码(p）。

因为，此时以s为树根的子树，在形成超级节点时。由于s为黑，且s的两个孩子也为黑色，所以s会单独形成超级节点，此时，它已经处于下溢的边界了。从而就不能再往外借出节点了。

但，可以从p所在的超级节点 借。（因为p为红色，所以它所在的超级节点中至少要有一个黑色节点，所以，借一个节点之后，不会引起该超级节点的下溢。）


  • 按照B-树的角度，此时需要进行合并（图b′）。即，将关键码p取出并下降一层，以p为粘合剂，将原左、右孩子合并为一个节点。
  • 从红黑树角度，这一过程等效的理解为（图b）：s与p互换颜色（即 s要变为红色）。

至此，红黑树条件亦必在全局得以恢复，删除操作即告完成。

5.2.3 双黑修正（BB-2B）：s黑，且两个孩子均为黑；p为黑

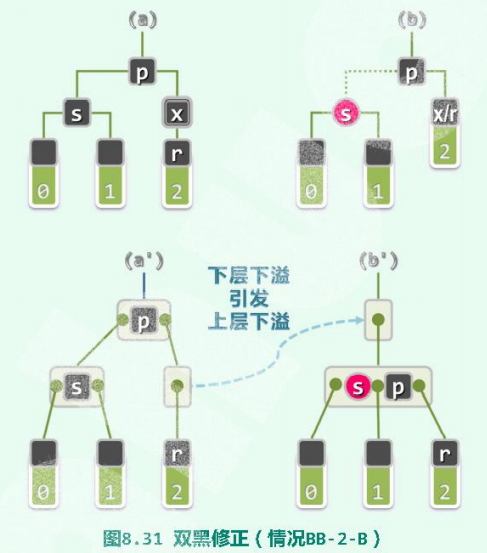
image.png
此时，因关键码x的删除，导致其所属节点发生下溢。

  • 此时需要进行合并（图b′）。即，将关键码p取出并下降一层，以p为粘合剂，将原左、右孩子合并为一个节点。
  • 从红黑树角度，这一过程等效的理解为（图b）：s需要变为红色。
  • 但是，这里的节点p在形成超级节点时，p将会单独形成超级节点（因为p以及它的左、右孩子均为黑色）。所以，p被借走时，p所在的超级节点，将会形成下溢。
    • 好在，此时可以集训分情况处理（即 递归调用 双黑处理函数solveDoubleBlack()）。高度地政，至多chapter8.3 红黑树(red-black tree) - 图14步。


5.2.4 双黑修正（BB-3）：s红，s左右孩子均为黑色

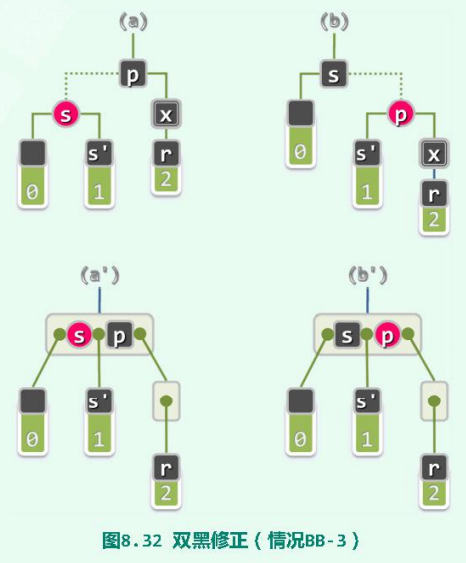
image.png
由于，s是红色，所以p一定是黑色。且此时，s的左、右孩子均为黑色；

  • 从B-树角度，只需要如图（b′）所示，令关键码s与p互换颜色。

  • 从红黑树角度，这一转换对应于以节点p为轴做一次旋转（zig或zag旋转），并交换s与p的颜色。

    至此，经过上述两步调整，双黑缺陷依然存在（子树r的黑高度并未复原），而缺陷位置的高度也并未上升。

    那这样的调整，有什么意义呢？

    • 在转换之后的红黑树中，被删除节点x（及其替代者节点r）有了一个新的兄弟**s'**，这个**s′**是**黑色**的了。接下来可以套用此前所介绍其它情况的处置方法，继续并最终完成双黑修正。
    • 同时，现在的节点p，也已经黑色转为**红色**。因此接下来即便需要继续调整，必然既不可能转换回此前的情况BB-3，也不可能转入可能需要反复迭代的情况BB-2B。实际上反过来，此后只可能转入更早讨论过的两类情况——BB-1或BB-2-R。

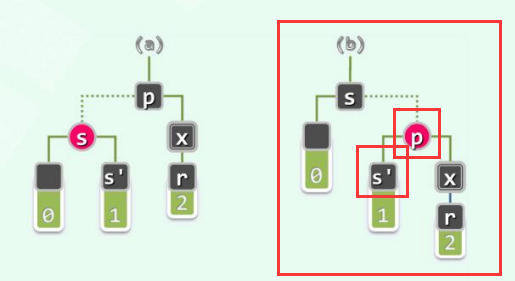
    image.png

  • 这就意味着，接下来至多再做一步迭代调整，整个双黑修正的任务即可大功告成。


5.2.5 归纳

以上的各种情况，可归纳为下图所示：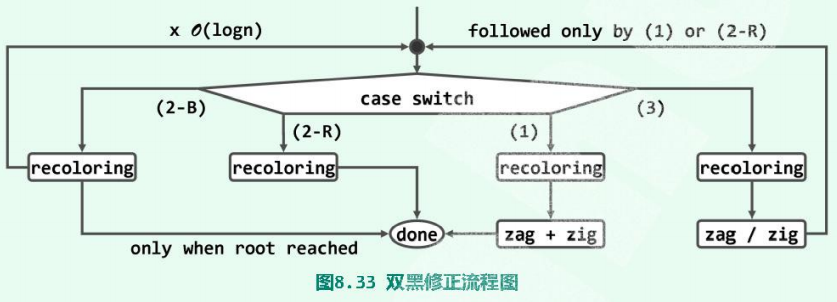
image.png
其中涉及的重构、染色等局部操作，均可在常数时间内完成，故为了估计整个双黑修正过程的时间复杂度，也只需统计这些操作各自的累计执行次数。具体统计可归纳为表8.2。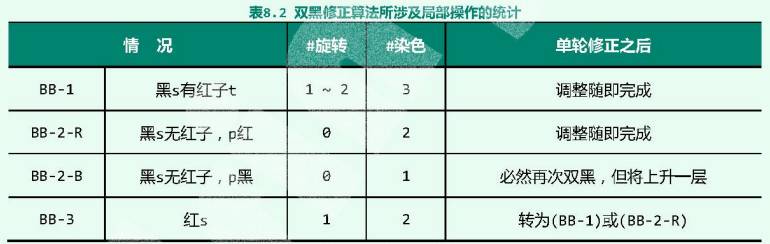
image.png
可见：

  • 前两种情况各自只需做一轮修正，最后一种情况亦不过两轮。
  • 情况BB-2-B虽可能需要反复修正，但由于待修正位置的高度严格单调上升，累计也不致过

O(logn)轮，故双黑修正过程总共耗时不超过O(logn)。即便计入此前的关键码查找和节点摘除
操作，红黑树的节点删除操作总是可在O``(logn)时间内完成。

纵览各种情况，不难确认：一旦在某步迭代中做过节点的旋转调整，整个修复过程便会随即完成。因此与双红修正一样，双黑修正的整个过程，也仅涉及常数次的拓扑结构调整操作。

这一有趣的特性同时也意味着，在每次删除操作之后，拓扑联接关系有所变化的节点绝不会超过常数个——这一点与AVL树（的删除操作）完全不同，也是二者之间最本质的一项差异。

5.2.6 代码

 /******************************************************************************************
 * RedBlack双黑调整算法：解决节点x与被其替代的节点均为黑色的问题
 * 分为三大类共四种情况：
 *    BB-1 ：2次颜色翻转，2次黑高度更新，1~2次旋转，不再递归
 *    BB-2R：2次颜色翻转，2次黑高度更新，0次旋转，不再递归
 *    BB-2B：1次颜色翻转，1次黑高度更新，0次旋转，需要递归
 *    BB-3 ：2次颜色翻转，2次黑高度更新，1次旋转，转为BB-1或BB2R
 ******************************************************************************************/

template<typename T>
void RedBlack<T>::solveDoubleBlack(BinNodePosi<T> r)
{
    BinNodePosi<T> p = r ? r->parent_ : hot_;  if (!p)    return; //r的父亲（如果p不存在，即r为树根。）
    /*问：为什么要判断r的父亲是否为空（p为空，表示r为根节点）？
    * 因为后面会有递归调用，有可能上升至树根处，所以需要判断是否为树根*/

    BinNodePosi<T> s = (r == p->lc_) ? p->rc_ : p->lc_; //s节点（r的兄弟）

    if (IsBlack(s)) //s为黑
    {
        BinNodePosi<T> t = nullptr; //s的红孩子（若左、右孩子，左者优先；皆黑时，为nullptr）
        if (IsRed(s->rc_))    t = s->rc_; //t是右孩子
        if (IsRed(s->lc_))    t = s->lc_; //t是左孩子

        if (t) //黑s 有 红孩子    BB-1
        {
            RBColor oldcolor = p->color_; //备份原子树根节点p的颜色，并对t及其父亲、祖先
            //以下，通过旋转重平衡，并将新子树的左右孩子染黑色
            BinNodePosi<T> b = FromParentTo(*p) = rotateAt(t); //旋转
            if (HasLChild(*b))
            {
                b->lc_->color_ = RB_BLACK;
                updateHeight(b->lc_); 
            }
            if (HasRChild(*b))
            {
                b->rc_->color_ = RB_BLACK;
                updateHeight(b->rc_);
            }

            b->color_ = oldcolor; // b继承p的颜色（即，新子树根节点 继承 原子树根节点的颜色）
        }
        else //黑s 无 红孩子
        {
            s->color_ = RB_RED; s->height_--; //s变为红色
            if (IsRed(p)) //BB-2R
            {
                p->color_ = RB_BLACK; //p转黑，但黑色高度不变（因为s由黑变红，p由红变黑）
            }
            else //BB-2B
            {
                p->height_--; //p还是黑色，但是其黑高度减一（因为s由黑变红）
                solveDoubleBlack(p); //递归上溯
            }
        }    
    }
    else //s为红色：BB-3
    {
        s->color_ = RB_BLACK; p->color_ = RB_RED; //s与p颜色互换（即：s由红转黑；p由黑转红）
        BinNodePosi<T> t = IsLChild(*s) ? s->lc_ : s->rc_; //取t 与其父亲s同侧

        hot_ = p; FromParentTo(*p) = rotateAt(t); //做zig或zag旋转

        solveDoubleBlack(r); //继续修正r处双黑---此时的p已经转红，故后续只能是BB-1或BB-2R
    }

}