算法

算法：即特定计算模型下，旨在解决特定问题的指令序列

• 输入：待处理的信息（问题）
• 输出：经处理的信息（答案）

正确性：的确可以解决指定的问题
确定性：任一算法都可以描述为一个由基本操作组成的序列。
可行性：每一基本操作都可实现，且在常数时间内完成。
有穷性：对任何输入，经有穷次基本操作，都可以得到输出。

时间复杂度

由于运行时间是由多种因素综合作用而决定的。

• 首先，同一算法，对于不同的输入所需的运行时间并不相同。

对于问题的规模的扩大，计算成本通常也呈上升趋势。

T(n)

执行时间的这一变化趋势可以表示为输入规模的一个函数，称作该算法的时间复杂度（time complexity）。具体地，特定算法处理规模为n的问题所需的时间可记作：T(n)

渐进复杂度：大记号

这种着长远、更为注重时间复杂度的总体变化趋势和增长速度的策略与方法，即所谓的渐进分析（asymptotic analysis）。

当输入规模n足够大，算法的执行时间T(n) 的渐进增长速度，应该如何度量和评价？
首先，关注T(n)的渐进上界。为此可引入所谓“大O记号”。具体地，若存在正的常数c和函数f(n)，使得对任何n>=2都有：T(n) <= c*f(n)
则可认为在n足够大之后，f(n)给出了T(n)增长速度的一个渐进上界。此时，记为：
T(n) = O(f(n))**

由这一定义，可导出大O记号的以下性质：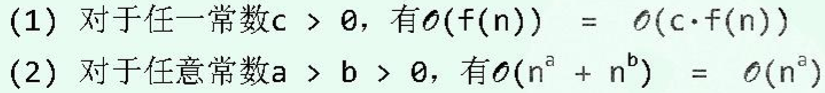

大Ω记号

为了对复杂度最好情况作出估计，需要借助大Ω符号。

如果存在正的常数c和函数g(n)，使得对于任何n≥2都有：

就可以认为在n足够大之后，g(n)给出了T(n)的一个渐进下界 ，此时，我们记为：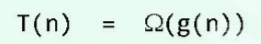

大O于大Ω的区别

大Θ记号

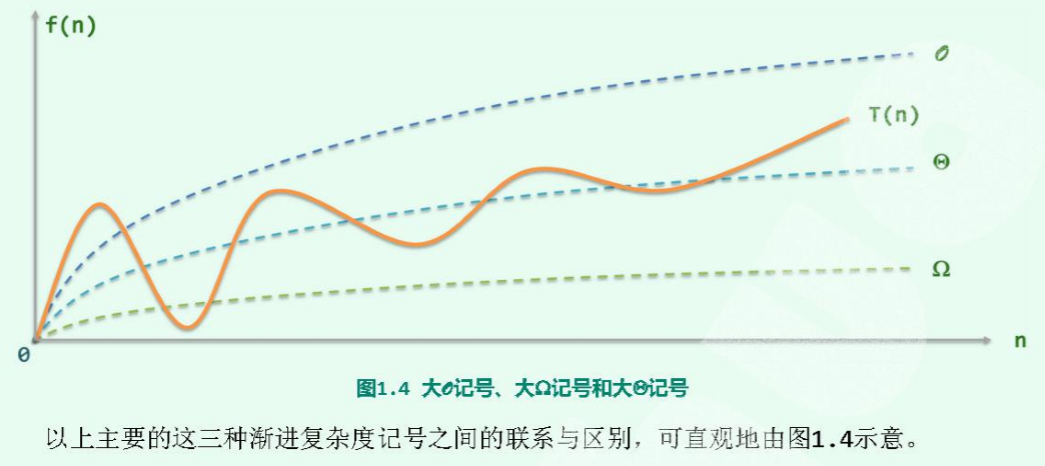
空间复杂度

实际上针对时间复杂度引入的几种渐进记号，也适用于对空间复杂度的度量。

空间复杂度通常不计入元时输入本身所占用的空间。