1. 栈
- 1.1. 栈的模板类的实现
- 1.2. 栈的应用
define N_OPTR 9 //运算符总数
- 1.2.4. 逆波兰表达式
  - 1.2.4.1 问题
  - 1.2.4.2. 逆波兰表达式的优点
- 1.2.5. 试探回溯法
2. 队列
- 2.1 队列的实现
- 2.2 队列的应用
  - 2.2.1 循环分配器
  - 2.2.2 银行服务模拟

参考文章：https://twinkle0331.github.io/stack.html

1. 栈

栈是存放数据结构的一种特殊容器，其中的数据元素按线性的逻辑次序排列，所以，也可定义首、末元素。

约定，只能从某一端进行插入、删除。禁止操作的另一端，称为盲端。
可以进行操作的一端称为，栈顶（stack top）；禁止操作的另一端也叫，栈底（stack bottom）。
栈中的元素遵循“后进先出（last in first out）”的原则。

1.1. 栈的模板类的实现

由于栈可看做序列的特例，所以我们可以使用前面章节中的：List 或者 Vector 来当做父类，进而派生出 “栈”类。

1、由List作为父类，来实现：

#include "../List/List.h" //根据目录结构
template<class T>
class Stack : public List<T>
{
    void push(const T& e)
    {
        insertAsLast(e);
    }
    T pop()
    {
        remove(last());
    }
    T& top()
    {
        return last()->data_;
    }
};

2、由Vector作为父类，来实现：

#include "../DSACPP/vector.h"
template<class T>
class Stack : public Vector<T>
{
public:
    void push(const T& e)
    {
        insert(size(), e);  //入栈，等效于：将新元素作为向量的末尾元素插入
    }
    T pop(const T& e)
    {
        return remove(size() - 1); //出栈，等效于：将向量中的末尾元素删除
    }
    T& top()
    {
        return (*this)[size() - 1];
    }
};

至此，模板类的实现的已经完成，下面来看一下，栈的应用。

1.2. 栈的应用

在栈擅长解决的典型问题中，有一类具有以下共同的特征：

首先，有明确的算法，但其解答却以线性序列的形式给出；
其次，无论是递归，还是迭代。该序列都是依逆序计算输出的；
最后，输入和输出规模不确定，难以事先确定盛放输出数据的容器大小。

因其特有的特征“后进先出”及其在容量方面的自适应性，使用栈来解决此类问题可谓恰到好处。

1.2.1. 逆序输出——进制转换

考虑如下问题，任给一个十进制整数n，将其转换为λ进制（在这里我们规定最大是16进制数）的表示形式：如12345 = 30071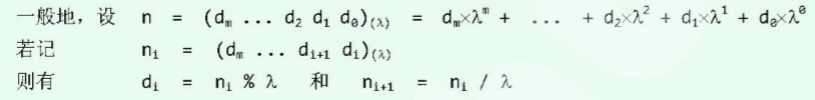

注意，上图中的：
n：表示十进制数
di：表示n第i次除以次λ后的余数
λ：将要转换为λ进制数
ni：表示n 第i次除以λ后的商
具体如下图所示：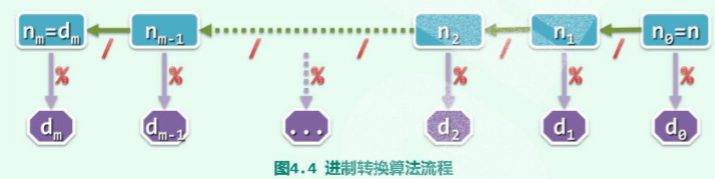

或者下面的形式：

由此，可写出其代码：

1.2.1.1. 递归版

void convert(Stack<char>& s, std::int_fast32_t n, int base)
{
    //assert((base > 1 && base <= 16) && "转换为的进制数应该在(1,16]区间。");
    static char digit[] ={ '0', '1', '2', '3', '4', '5', '6','7','8','9',
                            'A', 'B','C', 'D','E','F', };
    if (n > 0) //当还有余数时，反复的进行
    {
        s.push(digit[n % base]); //将每次除以λ之后的余数 入栈
        convert(s, n / base, base);
    }
}

然后，在依次的弹出栈中所有元素，所得的字符串就是十进制数n，对应的λ进制数。

1.2.1.2. 迭代版

void convert1(Stack<char>& s, std::int_fast32_t n, int base)
{
    static char digit[] = { '0', '1', '2', '3', '4', '5', '6','7','8','9',
                        'A', 'B','C', 'D','E','F', };
    while (n>0)
    {
        s.push(digit[n % base]);
        n /= base;
    }
}

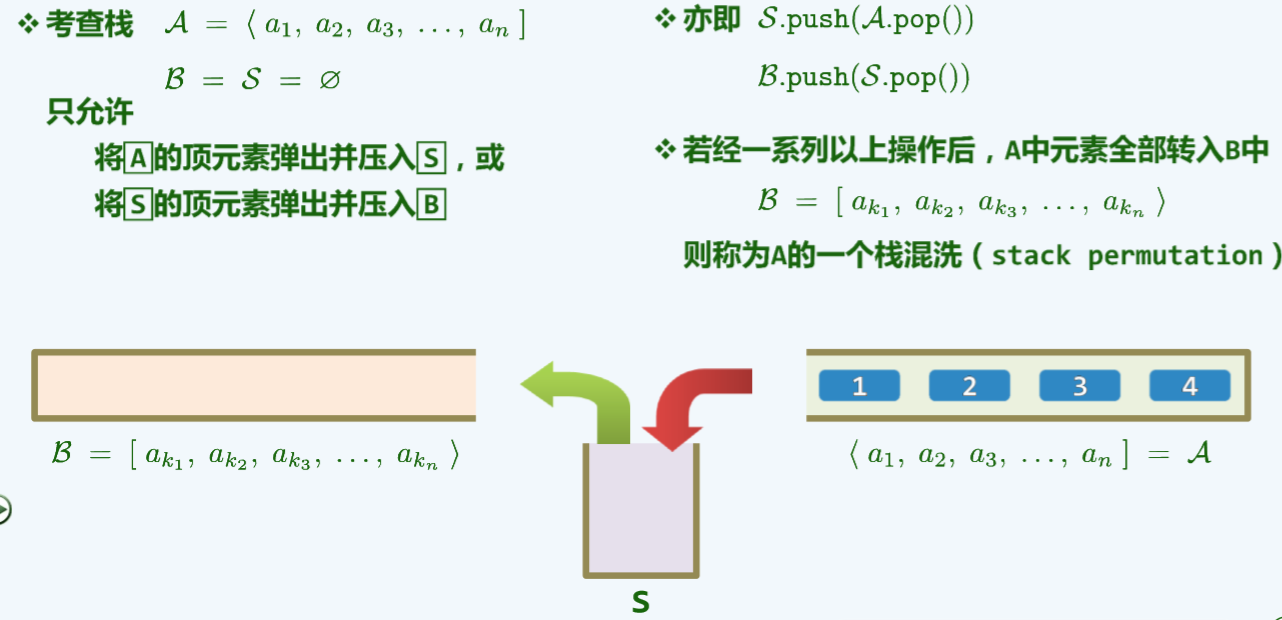
1.2.2. 栈混洗

尖括号：<表示栈顶，中括号：]表示栈底。

栈混洗定义

1.2.2.1 栈混洗的总数

对于长度为n的序列，它的栈混洗总数 SP(n)是多少呢？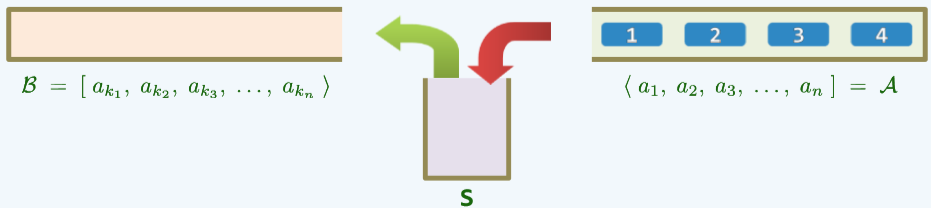

我们知道，当序列中只有一个元素，那对应的： SP(n) =1
对于这样的一个序列，假设第一个元素进入B栈时，在它进入之前已经有（K-1）个元素，则此时A栈中还剩余（n-k）个元素。注意，在B栈中的最靠底的（K-1）个元素，与A栈中还剩余（n-k）个元素它们之间的栈混洗是独立的。

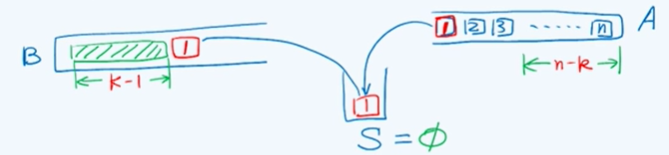
所以，此时该序列的栈混洗总数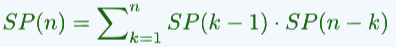：，**这对应的就是**卡特兰数，即，

**

1.2.2.2. 甄别是否为栈混洗

输入序列 <1，2，3，4，...，n] 的任意排列 [p1，p2，...，pn>是否为栈混洗？

简单的情况：当n=3时，<1，2，3]
- 栈混洗总数：6!/4!/3! = 5 种
- 全排列：3! = 6 种 // 也就是说，全排列种有一种排列不时栈混洗，它是： [3, 1, 2> | 为什么 [3, 1, 2> 不是它的栈混洗呢？
  观察：任意三个元素能否按某相对次序出现在栈混洗中，是与其它元素无关的。
  所以，可知对于，任何：1<=i <j <k <= n
  […，k，…，i，…，j，…]必非栈混洗
  
  证明过程，见：习题【4-3】
  由此，可得一个O(n3) **的甄别算法。（就是不断地枚举（i,j,k）的组合） | | —- |

实际上，进一步地，可以将判断依据作进一步的而简化。

在进一步的，我们可以得到一个O(n)的算法。该算法的思想： - 直接借助栈：A , B , S，模拟栈混洗过程，在每次S.pop()之前，检测S是否为空；或检测弹出的元素在S中，非顶端元素。

1.2.2.3. O(n) 的栈混洗甄别算法

思路还是：
直接借助栈：A , B , S，模拟栈混洗过程，在每次S.pop()之前，检测S是否为空；或检测弹出的元素在S中，非顶端元素。

这里设：设A为原始序列栈，B为要甄别的栈

先将要验证的栈B转移到rb栈中，这样B的栈底就位于rb的栈顶了，让我们可以知道依次放入栈B的元素是哪些。

模拟混洗的过程，如果rb栈顶与s中一样，那么就将rb和s都pop。

如果最后s为空，则表示能实现栈B这样一个结果。

// 参考：https://blog.csdn.net/ranjuese/article/details/104445070
template<typename T>
void check(Stack<T> A, Stack<T> B) //A为原序列，B为待检测的一个栈混洗
{
    Stack<T> rb, S; //栈B转移（复制一份）到栈rb；S为中转栈
    while (!B.empty()) //先将要验证的栈B转移到栈rb
    {
        rb.push(B.pop());
    }
    while (!A.empty())
    {
        S.push(A.pop());
        if (rb.top() == S.top()) //模拟混洗的过程，如果rb栈顶与s中一样，那么就将rb和s都pop。
        {
            rb.pop();
            S.pop();
        }
        while (!S.empty()) //当S栈中还有元素时，需要继续与rb栈中的栈顶元素比较是否相等
        {
            if (S.top() == rb.top())
            {
                rb.pop();
                S.pop();
            }
        }
    }
    return S.empty();  //最后，如果中转栈(S）为空，说明B是一个栈混洗，否则就不是
}

1.2.3. 延迟缓冲——中缀表达式求值

延迟缓冲：在线性扫描算法模式中，在预读足够长之后，方能确定可处理的前缀。

优先级
对于算式：(1+2)*3/5这样的表达式，有涉及到优先级的关系，我如何在代码中来对运算符知道它们的优先级呢？

答：将不同运算符之间的运算优先级关系，描述为一张二维表格： ```cpp
define N_OPTR 9 //运算符总数
typedef enum { ADD, SUB, MUL, DIV, POW, FAC, L_P, R_P, EOE } Operator; //运算符集合 //加、减、乘、除、乘方、阶乘、左括号、右括号、起始符与终止符

const char pri[N_OPTR][N_OPTR] = { //运算符优先等级 [栈顶] [当前] / |—————————— 当前运算符 ——————————| / / + - / ^ ! ( ) \0 / / — + / ‘>’, ‘>’, ‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘>’, ‘>’, / | - / ‘>’, ‘>’, ‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘>’, ‘>’, / 栈 / ‘>’, ‘>’, ‘>’, ‘>’, ‘<’, ‘<’, ‘<’, ‘>’, ‘>’, / 顶 / / ‘>’, ‘>’, ‘>’, ‘>’, ‘<’, ‘<’, ‘<’, ‘>’, ‘>’, / 运 ^ / ‘>’, ‘>’, ‘>’, ‘>’, ‘>’, ‘<’, ‘<’, ‘>’, ‘>’, / 算 ! / ‘>’, ‘>’, ‘>’, ‘>’, ‘>’, ‘>’, ‘ ‘, ‘>’, ‘>’, / 符 ( / ‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘=’, ‘ ‘, / | ) / ‘ ‘, ‘ ‘, ‘ ‘, ‘ ‘, ‘ ‘, ‘ ‘, ‘ ‘, ‘ ‘, ‘ ‘, / — \0 / ‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘ ‘, ‘=’ };

每一列代表：表达式中的 **当前运算符**；每一行代表：**操作符栈**中栈顶的可能的运算符。<br />可以看到，上面的表中，只有两处是“=”的，即：`(` =`)`；以及 `\0` = `\0` ：
- `(` =`)` 的情况：因为当 运算符栈中的 `(` 与当前运算符 `)` 相遇的时候，就说明 `(xxxxxx)`这个括号中的表达式已经被计算完了，所以此时，只需要将 这对括号丢弃即可。
- `\0` = `\0` 的情况：
**求值算法**<br />解决了优先级的问题，之后我们就可以开始写 **求值算法**：
- 我们将表达式中的：操作数、运算符  分别存放至不同的栈中。（比起将它们存入一个栈中，分开存放效率更高）。
> **何时开始子表达式的计算？**
> 主要就是看，运算符栈里面的运算符的优先级。运算符栈顶的元素，与当前扫描到的 运算符 进行优先级的比较：
> 1. 如果**当前运算符优先级较高**，则当前运算符入栈；
> 1. 如果**运算符栈的栈顶运算符优先级较高**，则运算符栈顶元素出栈 并与 操作数栈中的离栈顶最近的两个操作数 进行表达式计算。
> 
它就像下图表示的：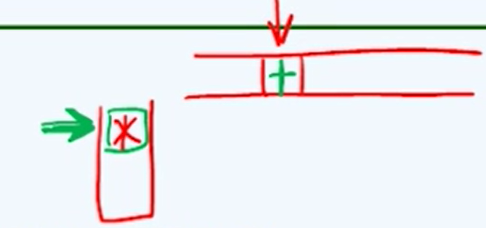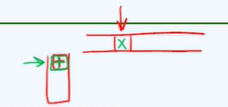
> ![image.png](https://cdn.nlark.com/yuque/0/2020/png/1282860/1593699685927-02e2ec10-1d92-480a-8488-410fdafe8a13.png#align=left&display=inline&height=114&margin=%5Bobject%20Object%5D&name=image.png&originHeight=228&originWidth=486&size=66019&status=done&style=shadow&width=243)                     ![image.png](https://cdn.nlark.com/yuque/0/2020/png/1282860/1593699756877-7b742f86-01f9-4595-a133-41247d8f60d3.png#align=left&display=inline&height=107&margin=%5Bobject%20Object%5D&name=image.png&originHeight=107&originWidth=228&size=15400&status=done&style=shadow&width=228)
> 运算符栈的栈顶元素优先级较高                                   当前运算符的优先级较高
- 对于 运算数栈 在存入运算数 之前，要先存入 “\0”，作为哨兵，来标志如果遇到它的时候表示整个表达式计算完成。
下面是整个算法代码：
```cpp
#define N_OPTR 9 //运算符总数
typedef enum { ADD, SUB, MUL, DIV, POW, FAC, L_P, R_P, EOE } Operator; //运算符集合
//加、减、乘、除、乘方、阶乘、左括号、右括号、起始符与终止符
const char pri[N_OPTR][N_OPTR] = { //运算符优先等级 [栈顶] [当前]
   /*              |-------------------- 当 前 运 算 符 --------------------| */
   /*              +      -      *      /      ^      !      (      )      \0 */
   /* --  + */    '>',   '>',   '<',   '<',   '<',   '<',   '<',   '>',   '>',
   /* |   - */    '>',   '>',   '<',   '<',   '<',   '<',   '<',   '>',   '>',
   /* 栈  * */    '>',   '>',   '>',   '>',   '<',   '<',   '<',   '>',   '>',
   /* 顶  / */    '>',   '>',   '>',   '>',   '<',   '<',   '<',   '>',   '>',
   /* 运  ^ */    '>',   '>',   '>',   '>',   '>',   '<',   '<',   '>',   '>',
   /* 算  ! */    '>',   '>',   '>',   '>',   '>',   '>',   ' ',   '>',   '>',
   /* 符  ( */    '<',   '<',   '<',   '<',   '<',   '<',   '<',   '=',   ' ',
   /* |   ) */    ' ',   ' ',   ' ',   ' ',   ' ',   ' ',   ' ',   ' ',   ' ',
   /* -- \0 */    '<',   '<',   '<',   '<',   '<',   '<',   '<',   ' ',   '='
};
/*注意：其中的一些函数来自RPN，也就是说这里顺带的将中缀表达式转化为RPN（后缀表达式）。
  如果单纯的求众追表达式的值，则可以去掉RPN部分*/
float evalute(char* S, char*& RPN)
{
    Stack<float> opnd; //运算数栈
    Stack<char>     optr; //运算符栈 
    optr.push('\0');
    while (!optr.empty()) //在运算符栈非空之前，逐个处理表达式各个字符
    {
        if (std::isdigit(*S)) //如果是数字，则将其读取至S栈中，并且将其添加至RPN尾部
        {
            readNumber(S, opnd);
            append(RPN, opnd.top());
        }
        else                 //若果当前字符为运算符，则
        {
            switch (orderBetween(optr.top(), *S))  //视其与运算符栈的栈顶运算符之间的优先级高低分别处理
            {
            case '<':    //栈顶运算符优先级更低时
                optr.push(*S); S++;    break; //计算推迟，当前运算符入栈
            case '>': { //栈顶运算符优先级更高时，可实施相应的计算，并将结果重新入栈
                char op = optr.pop();    append(RPN, op); //栈顶运算符出栈并续接至RPN末尾
                if (op == '!') //若属于一元运算符
                {
                    float pOpnd = opnd.pop(); //只需取出一个操作数，并
                    opnd.push(calcu(op, pOpnd)); //实施一元计算，结果入栈
                }
                else //对于其他二元运算符
                {
                    float pOpnd1 = opnd.pop(); float pOpnd2 = opnd.pop(); //取出 后、前操作数
                    opnd.push(calcu(pOpnd1, op, pOpnd2)); //实施二元计算，结果入栈
                }
                break;
            }
            default: std::exit(-1); //当语法错误时，不作处理，直接退出
            }
        }        
    }
    return opnd.pop(); //弹出并返回最后的计算结果
}
double calcu ( double a, char op, double b ) { //执行二元运算
   switch ( op ) {
      case '+' : return a + b;
      case '-' : return a - b;
      case '*' : return a * b;
      case '/' : if ( 0==b ) exit ( -1 ); return a/b; //注意：如此判浮点数为零可能不安全
      case '^' : return pow ( a, b );
      default  : exit ( -1 );
   }
}
double calcu ( char op, double b ) { //执行一元运算
   switch ( op ) {
      case '!' : return ( double ) facI ( ( int ) b ); //目前仅有阶乘，可照此方式添加
      default  : exit ( -1 );
   }
}
__int64 facI ( int n ) { __int64 f = 1; while ( n > 1 ) f *= n--; return f; } //阶乘运算（迭代版）
Operator optr2rank ( char op ) { //由运算符转译出编号
   switch ( op ) {
      case '+' : return ADD; //加
      case '-' : return SUB; //减
      case '*' : return MUL; //乘
      case '/' : return DIV; //除
      case '^' : return POW; //乘方
      case '!' : return FAC; //阶乘
      case '(' : return L_P; //左括号
      case ')' : return R_P; //右括号
      case '\0': return EOE; //起始符与终止符
      default  : exit ( -1 ); //未知运算符
   }
}
char orderBetween ( char op1, char op2 ) //比较两个运算符之间的优先级
{ return pri[optr2rank ( op1 ) ][optr2rank ( op2 ) ]; }
void append ( char*& rpn, double opnd ) { //将操作数接至RPN末尾
   char buf[64];
   if ( 0.0 < opnd - ( int ) opnd ) sprintf ( buf, "%f \0", opnd ); //浮点格式，或
   else                             sprintf ( buf, "%d \0", ( int ) opnd ); //整数格式
   rpn = ( char* ) realloc ( rpn, sizeof ( char ) * ( strlen( rpn ) + strlen ( buf ) + 1 ) ); //扩展空间
   strcat ( rpn, buf ); //RPN加长
}
void append ( char*& rpn, char optr ) { //将运算符接至RPN末尾
   int n = strlen ( rpn ); //RPN当前长度（以'\0'结尾，长度n + 1）
   rpn = ( char* ) realloc ( rpn, sizeof ( char ) * ( n + 3 ) ); //扩展空间
   sprintf ( rpn + n, "%c ", optr ); rpn[n + 2] = '\0'; //接入指定的运算符
}

该算法自左向右扫描表达式，并对其中字符逐一做相应的处理。那些已经扫描过但(因信息不足)尚不能处理的操作数与运算符，将分别缓冲至栈opnd和栈optr。
一旦判定已缓存的子表达式优先级足够高，便弹出相关的操作数和运算符，随即执行运算，并将结果压入栈opnd。
请留意这里区分操作数和运算符的技巧。一旦当前字符由非数字转为数字，则意味着开始进入一个对应于操作数的子串范围。由于这里允许操作数含有多个数位，甚至可能是小数，故可调用readNumber()函数(习题[4-6])，据当前字符及其后续的若干字符，利用另一个栈解析出当前的操作数。解析完毕，当前字符将再次聚焦于一个非数字字符。

1.2.4. 逆波兰表达式

逆波兰表达式（reverse polish notation，RPN）：是数学表达式的一种，其语法规则可概括为：

操作符紧邻于对应的（最后一个）操作数的后面。如：“12+”即通常习惯的“1+2”。

更多的例子

相对于日常使用的中缀表达式，RPN也称作：后缀表达式

日常使用的中缀表达式的运算规则为：分为两部分，即约定俗成的运算符优先级；强制指定的括号

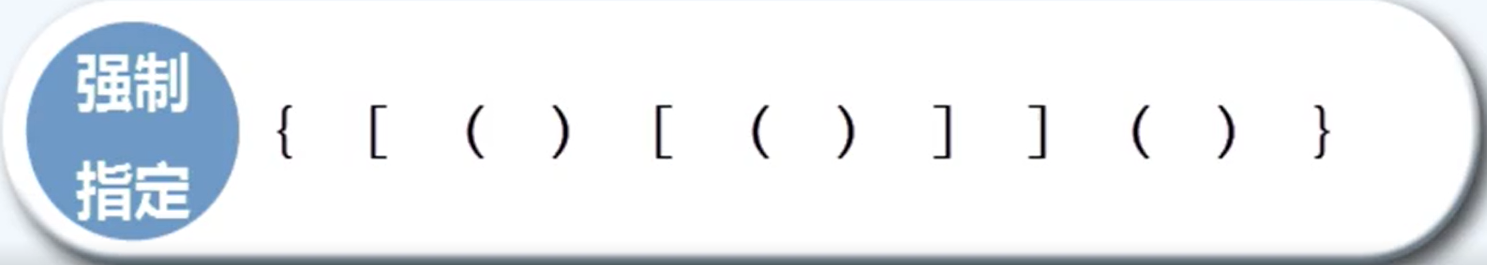
在RPN（后缀表达式）中运算符的执行次序，可更加简洁的确定。不需要要事先做任何约定，更无须借助括号强制改变优先级。

逆波兰表达式的代码实现，其实在3、延迟缓冲——中缀表达式求值中已经同时实现了。在这里，我们再次把主要实现逆波兰表达式的代码写一下：

void append ( char*& rpn, double opnd ) { //将操作数接至RPN末尾
   char buf[64];
   if ( 0.0 < opnd - ( int ) opnd ) sprintf ( buf, "%f \0", opnd ); //浮点格式，或
   else                             sprintf ( buf, "%d \0", ( int ) opnd ); //整数格式
   rpn = ( char* ) realloc ( rpn, sizeof ( char ) * ( strlen( rpn ) + strlen ( buf ) + 1 ) ); //扩展空间
   strcat ( rpn, buf ); //RPN加长
}

void append ( char*& rpn, char optr ) { //将运算符接至RPN末尾
   int n = strlen ( rpn ); //RPN当前长度（以'\0'结尾，长度n + 1）
   rpn = ( char* ) realloc ( rpn, sizeof ( char ) * ( n + 3 ) ); //扩展空间
   sprintf ( rpn + n, "%c ", optr );  //注意，这里添加了一个空格符
   rpn[n + 2] = '\0'; //接入指定的运算符
}

注意：关于sprintf ( rpn + n, "%c ", optr ); 中追加字符串的说明，请移步至此。

1.2.4.1 问题

1、RPN表达式无需括号即可确定运算优先级，是否意味着所占空间必少于常规表达式？
答：未必，尽管RPN表达式可省去括号，但是必须在相邻的操作数、操作符之间插入特定的分隔符(通常为空格)。这种分隔符必须事先约定，且不能用以表示操作符和操作数，故称为元字符。引入元字符的数目与操作数和操作符的数目相当，故所占空间未必少于原表达式。

2、既然evaluate()算法已经可以求值，同时完成RPN转换有何意义？
答：同样长度（指同样多操作数）的 RPN 比中缀表达式算得快。
若每个操作数都是一个具体的数，把中缀表达式转成 RPN 的过程已经足以得到中缀表达式的值，这种情况下转成 RPN 再计算得不偿失。

1.2.4.2. 逆波兰表达式的优点

当有操作符时就计算，因此，表达式并不是从右至左整体计算而是每次由中心向外计算一部分，这样在复杂运算中就很少导致操作符错误。
堆栈自动记录中间结果，这就是为什么逆波兰计算器能容易对任意复杂的表达式求值。与普通科学计算器不同，它对表达式的复杂性没有限制。
逆波兰表达式中不需要括号，用户只需按照表达式顺序求值，让堆栈自动记录中间结果；同样的，也不需要指定操作符的优先级。
机器状态永远是一个堆栈状态，堆栈里是需要运算的操作数，栈内不会有操作符。

1.2.5. 试探回溯法

回溯法，又称试探法，是常用的，基本的优选搜索方法。常用于解决这一类问题：给定一定约束条件F（该约束条件常用于后面的剪枝）下求问题的一个解或者所有解。

回溯法其实是暴力枚举的一种改进，因为其会聪明的filter（过滤）掉不合适的分支，大大减少了无谓的枚举。若某问题的枚举都是可行解得话，也就是没有剪枝发生，那么回溯法和暴力枚举并无二异。

该回溯法先从解空间中选取任意一个可能满足约束条件F的点x1,然后从满足F的解空间中继续选择一个点x2，直到所找到的点构成一个解S或者找不到满足约束条件F的点时，开始回溯。回溯到上一层节点f，再另选满足F的解空间中的一点，继续试探。

回溯法解决的问题的一般特征：能够利用约束条件F去快速判断构成一个完整解的一些局部候选信息partial candidates是否可能最终构成一个正确的、完整的解。

剪枝、试探、回溯
利用问题本身具有的某些规律尽可能多、尽可能早的排出搜索空间中的候选解。其中一种重要的技巧就是：根据候选解的某些局部特性，以候选解子集为单位批量的排出。通常如下图所示，搜索空间多呈树状结构，而被排出的候选解往往属于同一分支，所以这种技巧称为：剪枝。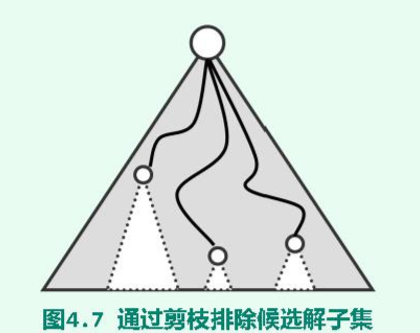

与之对应的算法多呈现为如下模式。
从零开始，尝试逐步增加候选解的长度。更准确地，这一过程是在成批地考察具有特定前缀的所有候选解。这种从长度上逐步向目标解靠近的尝试称为：试探。
作为解的局部特征，特征前缀在试探的过程中一旦被发现与目标解不合，则收缩到此前一步的长度，然后继续试探下一个可能的组合。特征前缀长度缩减的这类操作，称作回溯。其效果等同于剪枝。

2. 队列

与栈一样，队列也是存放数据对象的一种容器，其中的数据对象也按线性逻辑次序排列。同样只允许在队列两端进行操作，若插入对象只能从其中某一端，而删除只能从另外一端，将允许取出元素的一头称为队首，允许插入的一端称为队尾。队列中各对象的操作次序遵循先进先出的规律：先进先出（first in first out）。

2.1 队列的实现

可以借助之前章节的链表List类当做父类来实现。

// Queue.h
#ifndef DSACPP_QUEUE_QUEUE_H_
#define DSACPP_QUEUE_QUEUE_H_

#include "../List/List.h" //以链表为父类

template<class T>
class Queue : public List<T>
{
public: //size() empty() 沿用链表的
    void enqueue(const T& e) //入队
    {
        insertAsLast(e);
    }


    T dequeue() //出队
    {
        return remove(first());
    }


    T& front()  //队首
    {
        return first()->data_;
    }

};

#endif

2.2 队列的应用

2.2.1 循环分配器

一群客户共享同一资源时，按照先来后到的顺序分配资源，例如多个应用程序共享cpu，实验室成员共享打印机。

具体地，可以借助队列Q实现一个资源循环分配器，其总体流程大致如下：

RoundRobin //循环分配器
{
    Queue Q(clients); //参与资源分配器的所有客户组成队列

    while(!ServiceClosed()) //在服务关闭之前，反复地
    {
        e = Q.dequeue(); //队首的客户出队，并
        serve(e);   //接受服务。然后
        Q.enqueue(e); //重新入队
    }
}

2.2.2 银行服务模拟

以银行这一典型场景为例，利用队列结构实现队顾客服务的调度和优化。

通常，银行都设有多个窗口。顾客按照到达的顺序分别在各个窗口排队等待办理业务。为此，先定义顾客类Customer，来记录顾客所属的队列及其所办业务的服务时长：

struct Customer
{
    int window; //窗口编号
    unsigned int time; //服务时长
};

顾客在银行中接受服务整个过程，如下：

新来的顾客会寻找“最优的窗口（最短的队列）”，并入队。每一次最外的for循环都相当于过了一个单位的时间，所以，每个队列（窗口）的队首元素（第一个人）的服务时间都会减少一个单位时间。

void simulate(int nWin, int servTime) //按照指定窗口数，服务总时间模拟银行业务
{
    Queue<Customer>* windows = new Queue<Customer>[nWin]; //为每一个窗口创建一个队列
    for (int now = 0; now < servTime; ++now) //在下班之前，每个一个单位时间
    {
        if (rand() % (1 + nWin)) //新顾客以nWin/(nWin + 1)的概率到达
        {
            Customer c; c.time = 1 + rand() % 98; //新顾客到达，服务时长随机
            c.window = bestWindow(windows, nWin); //找出最佳（最短）服务窗口
            windows[c.window].enqueue(c); //新顾客加入相应的队列
        }

        for (int i = 0; i < nWin; ++i) //分别检查
        {
            if (!windows[i].empty()) //每个非空队列
            {
                if (--windows[i].front().time <= 0) //队首顾客的服务时间减少一个单位
                    windows[i].dequeue();  //此时，队首顾客的业务办理完成，出列
            }
        }
    } //for
    delete[] windows; //释放所有队列（此前，~List会自动清空队列）
}

//这里的 最优队列，遵循的是：队列最短则为最优队列
void bestWindow(Queue<Customer> windows[], int nWin) //为新到的顾客确定最佳队列
{
    int minsize = windows[0].size(); 
    int optiWin = 0; //最优队列（初始为第0个队列是最优）

    for (int i = 1; i < nWin; ++i)
    {
        if (minsize > windows[i].size())
        {
            minsize = windows[i].size();
            optiWin = i;
        }    
    }

    return optiWin;
}

数据结构与算法

chapter4 栈与队列

1. 栈

1.1. 栈的模板类的实现

1.2. 栈的应用

1.2.1. 逆序输出——进制转换

1.2.1.1. 递归版

1.2.1.2. 迭代版

1.2.2. 栈混洗

1.2.2.1 栈混洗的总数

1.2.2.2. 甄别是否为栈混洗

1.2.2.3. O(n) 的栈混洗甄别算法

1.2.3. 延迟缓冲——中缀表达式求值

define N_OPTR 9 //运算符总数

1.2.4. 逆波兰表达式

1.2.4.1 问题

1.2.4.2. 逆波兰表达式的优点

1.2.5. 试探回溯法

2. 队列

2.1 队列的实现

2.2 队列的应用

2.2.1 循环分配器

2.2.2 银行服务模拟

chapter4 栈与队列

1. 栈

1.1. 栈的模板类 的实现

1.2. 栈的应用

1.2.1. 逆序输出——进制转换

1.2.1.1. 递归版

1.2.1.2. 迭代版

1.2.2. 栈混洗

1.2.2.1 栈混洗的总数

1.2.2.2. 甄别是否为栈混洗

1.2.2.3. O(n) 的栈混洗甄别算法

1.2.3. 延迟缓冲——中缀表达式求值

define N_OPTR 9 //运算符总数

1.2.4. 逆波兰表达式

1.2.4.1 问题

1.2.4.2. 逆波兰表达式的优点

1.2.5. 试探回溯法

2. 队列

2.1 队列的实现

2.2 队列的应用

2.2.1 循环分配器

2.2.2 银行服务模拟

1.1. 栈的模板类的实现