你背不下来的书，总有人能背下来；你做不出来的题，总有人能做出来；你愿意拖到明天的事，总有人今天努力做完；那么不好意思，你想去的学校也只能别人去了，你想过的人生也只能别人过了。


路虽然很漫长，很孤单，但是只要你走出一步，你离目的地就近一步，千万不能停在原地叹息，否则永远都无法到达目的地。

Algorithm

没有哪个大牛对数据结构和算法是不熟练的。LeetCode 算法题，至少一题

1. 爬楼梯

动态规划看的有点懵逼，所以找这类题目刷一下，先刷简单的找找感觉吧。可以参考下这个博主的文章动态规划前人帮我们总结了以下几个特点：

  1. 本质上是用空间换时间
  2. 把历史记录保存起来，一般是用一个一维数组或者二维数组
  3. 把大问题拆成小问题
  4. 一般都会给数组初始值赋值

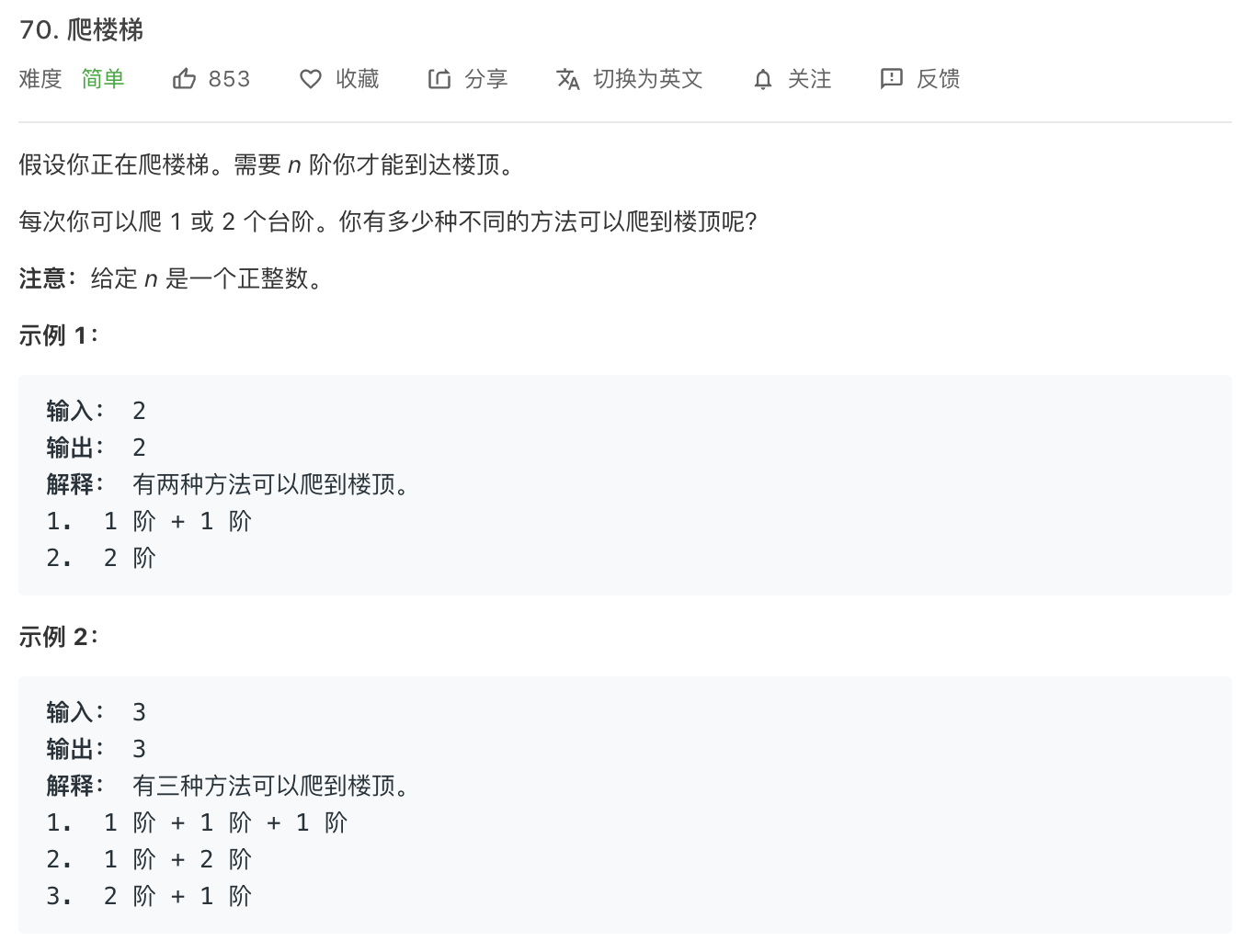
image.png
解：一次可以爬 1 或 2 个阶梯。我们假设 dp[n] 有 n 种方法，那么可以得出：dp[n-1]= n-1,dp[n-2]=n-2。如果要想爬到第 n 个阶梯，就只有两种方式，不是 n-1，就是 n-2。现在求所有的方法，可以得出等式：dp[n] = dp[n-1] + dp[n-2];

下面开始尝试找出特殊情况：
当 n = 1：
dp[1] = dp[0] + dp[-1]，数组下标不能为负数，而且 n=1 就只有一种跳法，所以 dp[1] = 1;

当 n = 2:
dp[2] = dp[1] + dp[0]，可以得出 dp[2] = 1，但是显然dp[2] 不等于 1，应该是 2，所以 dp[2] = 2;

当 n = 3:
dp[3] = dp[2] + dp[1]，带入上述值，得到 dp[3]=3，在纸上排列组合下，确实等于3，所以 dp[3]=3；

当 n = 4:
… 也符合上述推算结果。

下面就可以写代码了：

  1. int climbStairs(int n ){
  2.     if(n <= 2) {
  3.         return n;
  4.     }
  5.     // 先创建一个数组来保存历史数据
  6.     int[] dp = new int[n+1];
  7.     // 特殊情况提前给出初始值
  8.     dp[0] = 0;
  9.     dp[1] = 1;
  10.     dp[2] = 2;
  11.     // 通过关系式来计算出 dp[n]
  12.     for(int i = 3; i <= n; i++){
  13.         // 每次将算过的保存起来
  14.         dp[i] = dp[i-1] + dp[i-2];
  15.     }
  16.     // 把最终结果返回
  17.     return dp[n];
  18. }

做完这道题，确实可能对前面提到的动态规划那几个特点稍微的有了点感觉，例如空间换时间，初始化特殊值，大问题拆解小问题，利用历史数据。可以一鼓作气继续再刷几道题慢慢加大难度。

2.不同路径

这题还是用动态规划来做。难度是中等。
image.png

先分析题目，是不是一个二维坐标，我们可以用二维数组来表示，也就是说机器人从左上角走到左下角(i,j)有多少种走法？我们假设有 dp[i][j] 种路径，由于数组下标是从0开始，所以 dp[i-1][j-1] 是我们要的结果。

跟爬楼梯的例子一样，要想走到 (i,j) 这个位置有两种走法，一种是 dp[i-1][j] ，一种是 dp[i][j-1]，现在也是求所有的路径方法，可以得出 dp[i][j] = dp[i-1][j] + dp[i][j-1]。

下面开始尝试找出特殊情况并初始化：

当 i 或 j 任意一个为 0 时：
不成立，因为有负数了，这时它们的初始值都是1 ，例如 i=1,j=0,就只有1条路可以走，所以得出 d[0][j-1] = 1，d[i-1][0] = 1

代码：

  1. public  int uniquePaths(int m, int n) {
  2.     if (m <= 0 || n <= 0) {
  3.         return 1;
  4.     }
  6.     int[][] dp = new int[m][n];
  7.     // 初始化
  8.     for(int i = 0; i < m; i++){
  9.         dp[i][0] = 1;
  10.     }
  11.     for(int i = 0; i < n; i++){
  12.         dp[0][i] = 1;
  13.     }
  14.     // 有0的下标都初始为1了，所以从1开始
  15.     for (int i = 1; i < m; i++) {
  16.         for (int j = 1; j < n; j++) {
  17.             dp[i][j] = dp[i-1][j] + dp[i][j-1];
  18.         }
  19.     }
  20.     // 网格是从1开始的，数组是从0开始的，所以这里数组下标都要减1
  21.     return dp[m-1][n-1];
  22. }

Review

流畅的阅读英文技术资料是一个大牛必备的。英文学习，以技术翻译为主

这是一篇关于如何编写以太坊智能合约的教程，文章太长，单独用一篇来写。点击查看。

Tip

保持好奇，保持学习。至少一个技巧，以技术技巧为主

这周学习了 Solidity 的语法，准备些合约。这个教程不错。

Share

要是为了建立你的影响力，能够输出价值观。分享一篇有观点和思考的文章，也可以是技术总结的文章。

这周电话面试了，复盘了下面试的题目，高大上的技术问的少，底层基础的问的多。