0x00 随机事件及其概率

1、随机事件的几个基本概念

  • 随机事件(random event): 在同一组条件下, 每次试验可能出现也可能不出现的事件, 也叫偶然事件
  • 必然事件(certain event): 在同一组条件下, 每次试验一定出现的事件
  • 不可能事件(impossible event): 在同一组条件下, 每次试验一定不出现的事件
  • 样本空间: 一个试验中所有的简单事件的全体集合称为样本空间或基本空间, 记为 Ω
  • 样本点：样本空间中每一个特定的试验结果
  • 随机事件简称事件, 用大写字母A, B, C等表示;
  • 必然事件用Ω表示, 不可能事件用Φ表示
  • 如果一个事件不能分解成两个或多个事件, 则这个事件称为基本事件(elementary event)或简单事件

image.png

2、事件的概率

事件 A 的概率是事件 A 在随机试验中出现的可能性大小的数值度量，记事件 A 发生的概率为 P(A)。
基于对概率的不同解释，概率的定义有所不同，主要有古典定义、统计定义和主观概率定义。
（1）概率的古典定义
如果一项随机试验的全部基本事件总数有限，而且各个基本事件出现的可能性相等，则某一事件 A 发生的概率为该事件所包含的基本事件数 m 与样本空间中所包含的基本事件总数 n 的比值，记为：P(A)＝事件 A 所包含的基本事件的个数/样本空间所包含的基本事件的个数＝m/n
（2）概率的统计定义
在相同条件下重复进行的 n 次试验中，事件 A 出现 m 次(m≤n), 称比值 m/n 为事件 A 发生的频率。当实验次数 n 很大时，该频率稳定地在某一常数 p 上下波动，且波动的幅度随试验次数的增加而减小，则定义频率的稳定值 p 即为事件 A 的概率，记为：P(A)＝m/n＝p。
（3）主观概率定义
主观概率指的是一个决策者根据本人掌握的信息对某个事件发生可能性作出的判断，对一些无法重复的试验，只能根据以往的经验，人为确定这个事件的概率。

0x01 概率的性质和运算法则

1、概率的基本性质

（1）对任一随机事件 A，有 0≤P（A）≤1
（2）必然事件的概率为 1，而不可能事件的概率为 0，即 P（Ω）＝1，P（Φ）＝0
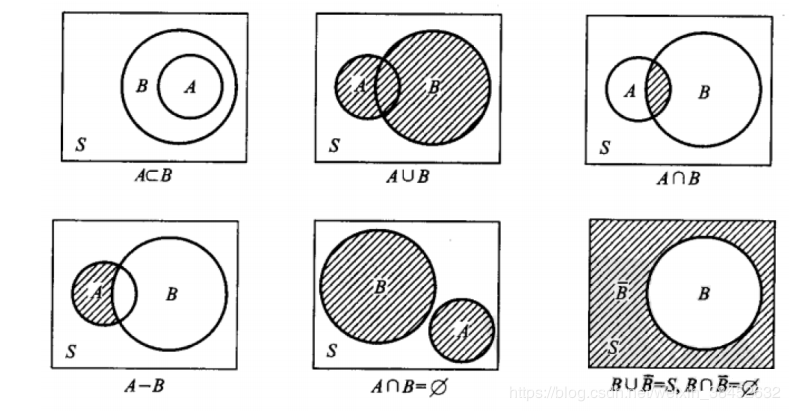
image.png
image.png
image.png

2、概率的加法法则

法则 1 两个互斥事件之和的概率等于两个事件概率之和

  • 设 A 和 B 为两个互斥事件，则
    • P(AUB)＝P(A)＋P(B)
  • 对于多个两两互不相容的随机事件 A1, A2, …, An，则
    • P(A1UA2…UAn)＝P(A1)＋P(A2)…＋P(An)
  • 其中必有一个发生的两个互斥事件叫做对立事件，记事件 A 的对立事件为: ‾A; 对 A 和‾A两个事件来说，则有
    • P(A)＝1－P(A)

法则 2 对于任意两个随机事件，它们和的概率为两个事件分别的概率之和减去两事件之交的概率。即
P(AUB)＝P(A)＋P(B)－P(AΠB)

3、条件概率与独立事件

（1）条件概率
当某一事件 B已经发生时，求事件 A发生的概率，称这种概率为事件 B发生条件下事件 A 发生的条件概率，
记为 P(A|B) 一般来说, P(A|B)≠P(A), 只有当 A 与 B 独立时，P(A|B)＝P(A)
（2）乘法公式
条件概率 P(A|B)与概率 P(AB)，P(B)的关系：
P(A|B)＝P(AB)/P(B), P(B)＞0
则概率的乘法公式为：P(AB)＝P(B)P(A|B) 或 P(AB)＝P(A)P(B|A)
（3）独立性
独立事件：若两个事件同时发生的概率等于它们各自发生的概率之积。即：
P(AB)＝P(A)·P(B)，则称事件 A 和事件 B 相互独立。
两个事件相互独立可推广到多个事件相互独立，若 P(A1A2…An)＝P(A1)P(A2)…P(An) 则称 A1,A2,…,An 相互独立
相依事件: 一个事件的发生与否会影响另一个事件的发生。
独立性与事件的互斥（互不相容）事件的关系: 互斥概率大于 0 的事件一定是相互依赖（不独立）的, 但相互依赖的事件不一定是互斥的; 不互斥事件可能是独立的, 也可能是不独立的, 然而独立事件不可能是互斥的。

4．全概率公式与贝叶斯公式

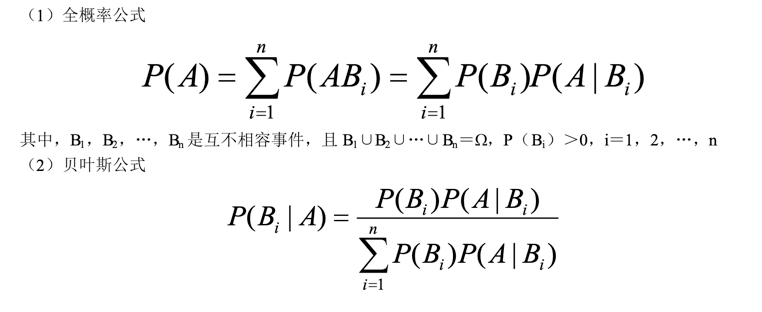
image.png

0x02 离散型随机变量及其分布

1．随机变量的概念

（1）随机事件的数量化为了把随机事件数量化，以便作数学上的处理，有必要把不采用数量标识表示化为采用数量标识表示。
（2）随机变量的定义
在相同条件下，如果每次试验可能出现不同的结果，把所有的结果都列举出来，即把 X 的所有可能值 x1，x2，„，xn 都列举出来，且 X 的可能值具有确定概率 P（x1），P（x2），„，P（xn），其中 P（xi）＝P（X＝xi）称为概率函数，则 X 称为 P（X）的随机变量，P（X）称为随机变量 X 的概率函数。
（3）两种类型的随机变量
① 离散型随机变量如果随机变量 X 只能取有限个或可数个值，则称 X 为离散型随机变量。
② 连续型随机变量如果随机变量 X 可以取一个或多个区间中的任何值，则称 X 为连续型随机变量。

2．离散型随机变量的概率分布

（1）离散型随机变量的概率分布
image.png

（2）离散型随机变量的期望值和方差
① 期望值
离散型随机变量 X 的数学期望是 X 所有可能取值 xi 与其对应概率 pi 的乘积之和，记作 E（X）或 μ。它表示随机变量本身的平均水平或集中程度。
image.png
② 方差与标准差
image.png
③ 离散系数
离散系数可用来比较不同期望值的总体之间的离中趋势。计算公式为：V＝σ/E（X）
④ 均值和方差
在财务分析中的应用在财务分析中，风险的概念十分重要。风险的高低有时可以单凭主观的感觉作出判断，也可以用方差或标准差去测量，从而得出一个比较客观和科学的结果。
image.png
（3）几种常见的离散型概率分布
① 0-1 分布
贝努里试验的特点：
a．试验包含了 n 个相同的试验；
b．每次试验只有两个可能的结果：“成功”或“失败”；
c．出现“成功”的概率 p 对每一次试验是相同的，“失败”的概率 q 也不变，且 p＋q＝1；
d．试验是互相独立的；
e．试验“成功”或“失败”可以计数，即试验结果对应于一个离散型随机变量。
若定义一次伯努利试验成功的次数为离散型随机变量 X，它的概率分布就是最简单的一个分布类型，即两点分布，亦称伯努利分布。
如果随机变量 X 只可能取 0 和 1 两个值，它们的概率分布为
P（X＝1）＝p，P（X＝0）＝1－p＝q
或 P（X＝x）＝pxq1－x（0＜p＜1），（x＝0，1）
则称 X 服从参数为 p 的 0-1 分布，也称两点分布。
0-1 分布的期望值和方差分别为：E（X）＝p，D（X）＝pq。
② 二项分布
Snip20191119_13.png
二项分布的期望值和方差分别为：E（X）＝np，D（X）＝npq。
③ 泊松分布(Poisson Distribution)
泊松分布是用来描述在一指定时间段或在一定空间区域或其他特定单位内某一事件出现的次数的分布，仅取非负整数。
(通常被使用在估算在 一段特定时间/空间内 发生事件 数量的概率)
使用泊松分布需要满足的前提条件:

  • 在 两个 相同大小/长度的 时间/空间内, 一个事件的发生的概率是相同的
  • 事件发生与不发生是相互独立的\不受其他事件的发生或者不发生影响

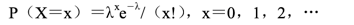
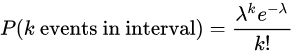
泊松分布的公式为：image.png
image.png
式中，λ 为给定的时间间隔内事件出现的平均数。
泊松分布的期望值和方差分别为：
E（X）＝λ
D（X）＝λ
在 n 重贝努利试验中，当“成功”的概率很小（即 p→0），试验次数很大时，二项分布可近似等于泊松分布，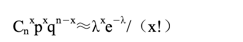
image.png
在实际应用中，当 p≤0.25，n＞20，np≤5 时，用泊松分布近似二项分布效果良好

  1. 例子1:  时间段
  2. 1). 背景: 我们想要测量 某餐厅 drive-through 周末早上, 15 分钟间隔内 顾客的人数.
  3. 假设顾客在不同的15分钟间隔内到达餐厅的概率是相同的,并且相互不影响,这样我们就可以使用Poisson Distribution,
  4. 根据历史数据 周末早上15 分钟间隔内到达餐厅的人数平均值是 10, 在这种情况下我们能构建
  5. PMF
  6. P(X) = (10^x * e^-10) / x!
  9. 2). 根据1) 我们可以知道 以 15分钟为间隔的来5个顾客的概率是 0.0378, 但是如果我们想要知道 以 3 分钟Wie间隔的来5个顾客的概率呢?
  10. 解:  我们可以根据历史数据 计算每分钟来的人数 10 / 15 = 2/3; 然后 2/3 * 3 计算出 历史数据 3mins间隔下的顾客人数为2. 使用 P( 5 )计算出相对应的概率.
  11. P(5) = (10 ^ 5 * e ^-10)/5! = 0.0378
  13. 例子2: 长度/距离
  14. 背景: 我们想要知道新建的高速公路上每隔3英里, 产生的会有多少个坑, ( 前提条件不赘述), 根据历史数据, 
  15. 每英里会有2 个坑, 则平均为 6. 构建
  16. PMF (x) = (6^x * e^-6) / x!

④ 超几何分布
设有 N 件产品，其中有 M 件次品，现从中任取 n 件（假定，n≤N），则在这 n 件中所含的次品件数 X 是一个随机变量，X 的概率函数为：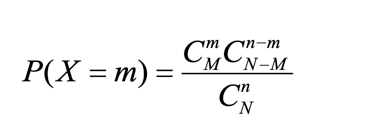
image.png
式中，m 为任取 n 件中次品的件数。则称 x 服从参数为 n，N，M 的超几何分布。
对于抽样问题来说，当原产品的批量相当大时，“无放回”可以当作“有放回”来处理，即此时可用二项分布近似超几何分布。

0x03 连续型随机变量的概率分布

1．概率密度与分布函数

image.png

2．正态分布

（1）正态分布的定义及图形特点
image.png
（2）标准正态分布
image.png
（3）正态分布表

  • 只要将一般正态分布转化为标准正态分布，通过查表，就可解决正态分布的概率计算问题。对于负的 x 值，可由 Φ（－x）＝1－Φ（x）得到。

（4）正态分布在质量管理中的应用
若 X～N（μ，σ2）时，有
P（|X－μ|≤σ）＝0.6826
P（|X－μ|≤2σ）＝0.9545
P（|X－μ|≤3σ）＝0.9973
可以认为 X 的值几乎一定落在区间（μ－3σ，μ＋3σ）内，这在全面质量管理中称作“3σ 准则”。
当今风靡全球的六西格玛管理质量标准也是在正态分布原理基础上建立的。当上下公差不变时，6σ 的质量水准就意味着产品合格率达到 99.9999998%，即 P（|X－μ|≤6σ）＝0.999999998，其特性值落在（μ－6σ，μ＋6σ）外的概率仅为十亿分之二。
（5）二项分布的正态近似
设随机变量 X～B（n，p），由中心极限定理，当样本量 n 越来越大时，则对任意 x，有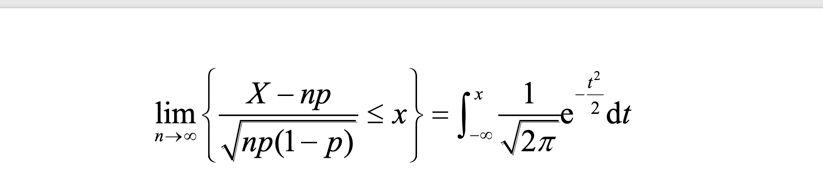
image.png
即当 n 很大，而 0＜p＜1 是一个定值时，服从二项分布的随机变量 X 近似服从正态分布 N（np，np（1－p））。

0x04 代码实现

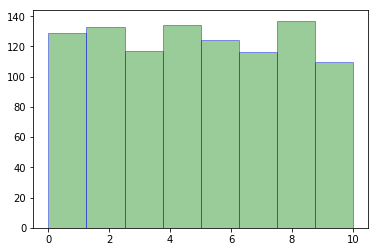
1、均匀分布

import random
import numpy as np

# np.random.uniform(low,high,size)  low和high为分布范围, size为样本数目
list_c = np.random.uniform(0,10,1000)
plt.hist(list_c,bins=8,color='g',alpha=0.4,edgecolor='b')
plt.show()

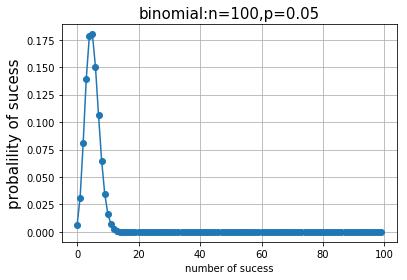
image.png

2、二项分布

import numpy as np
import matplotlib.pyplot as plt 
import math
from scipy import stats

n = 100 
p = 0.05
k = np.arange(0,n)
binomial = stats.binom.pmf(k,n,p)
plt.plot(k,binomial,'o-')
plt.title('binomial:n=%i,p=%.2f'%(n,p),fontsize=15)
# plt.xlabel('number of sucess',fontproperties='SimHei')
plt.xlabel('number of sucess')
plt.ylabel('probalility of sucess',fontsize=15)
plt.grid(True)
plt.show()

image.png

3、正态分布

X = np.random.normal(0, 1, 1000)  # 获取一组均值为0, 方差为1, 1000个对象 的正态分布的数组
# normal(loc=0.0, scale=1.0, size=None)
# loc：均值，scale：标准差，size：抽取样本的size
Y = np.random.normal(0, 1, 1000)

plt.scatter(X, Y, alpha=0.5)  # alpha透明度
plt.show()

image.png

plt.hist(X,bins=8,color='g',alpha=0.4,edgecolor='b')
plt.show()

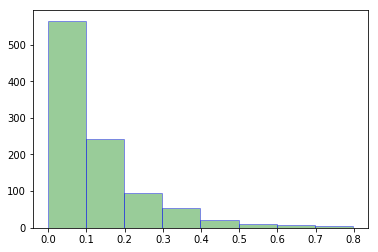
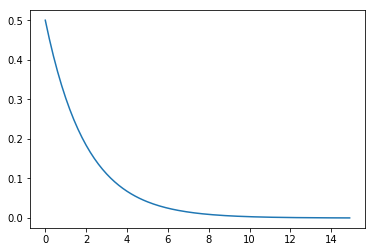
image.png

4、指数分布

lambd = 0.5
x = np.arange(0, 15, 0.1)
y = lambd * np.exp(-lambd * x)
plt.plot(x,y)
plt.show()

image.png

list_e = np.random.exponential(0.125,1000)
plt.hist(list_e,bins=8,color='g',edgecolor='b',alpha=0.4)
plt.show()

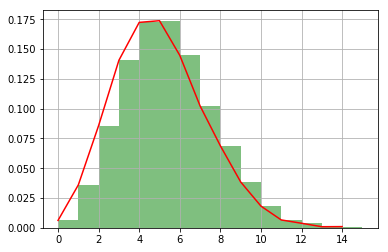
image.png

5、泊松分布

# Poisson分布
x = np.random.poisson(lam=5, size=10000)  # lam为λ size为k
pillar = 15
a = plt.hist(x, bins=pillar, normed=True, range=[0, pillar], color='g', alpha=0.5)
plt.plot(a[1][0:pillar], a[0], 'r')
plt.grid()
plt.show()

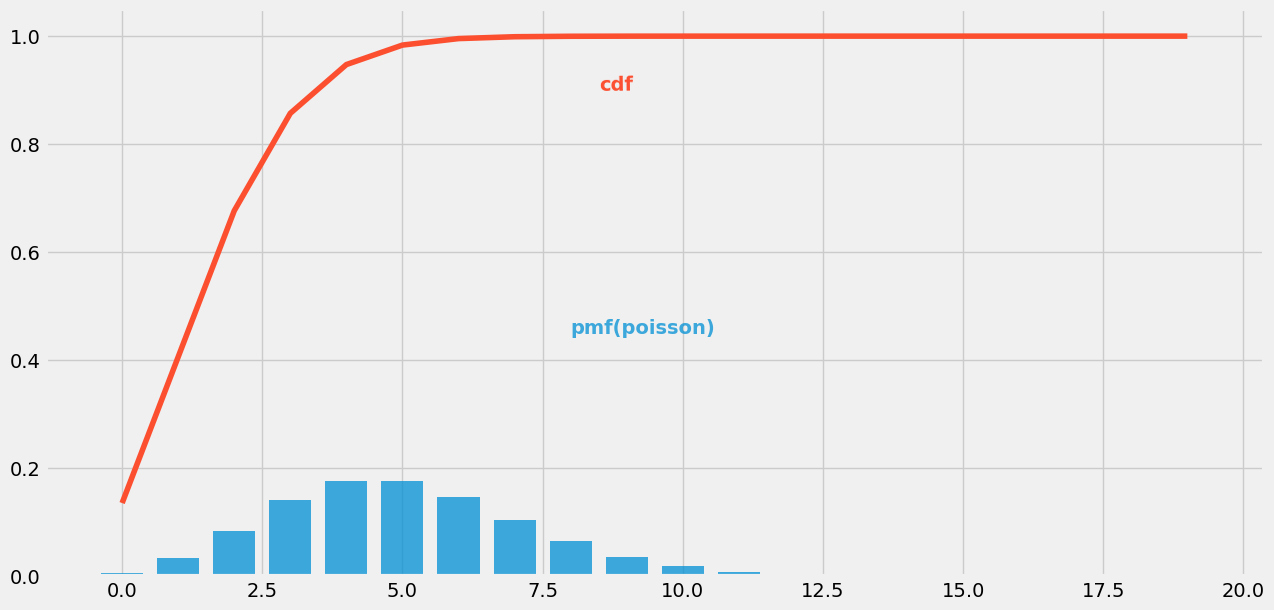
image.png

# 泊松分布——绘图
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML

# PLOTTING CONFIG 绘图配置
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams['figure.figsize']=(14,7)
plt.figure(dpi=100)

# PDF 绘制泊松分布的概率密度函数
plt.bar(np.arange(20), height=(stats.poisson.pmf(np.arange(20), mu=5)), width=0.75, alpha=0.75)

# CDF 绘制泊松分布的累计概率曲线
plt.plot(np.arange(20), stats.poisson.cdf(np.arange(20), mu=2), color="#fc4f30")

# LEGEND 图例
plt.text(x=8, y=0.45, s="pmf(poisson)", alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=8.5, y=0.9, s="cdf", rotation=0.75, weight="bold", color="#fc4f30")

plt.show()

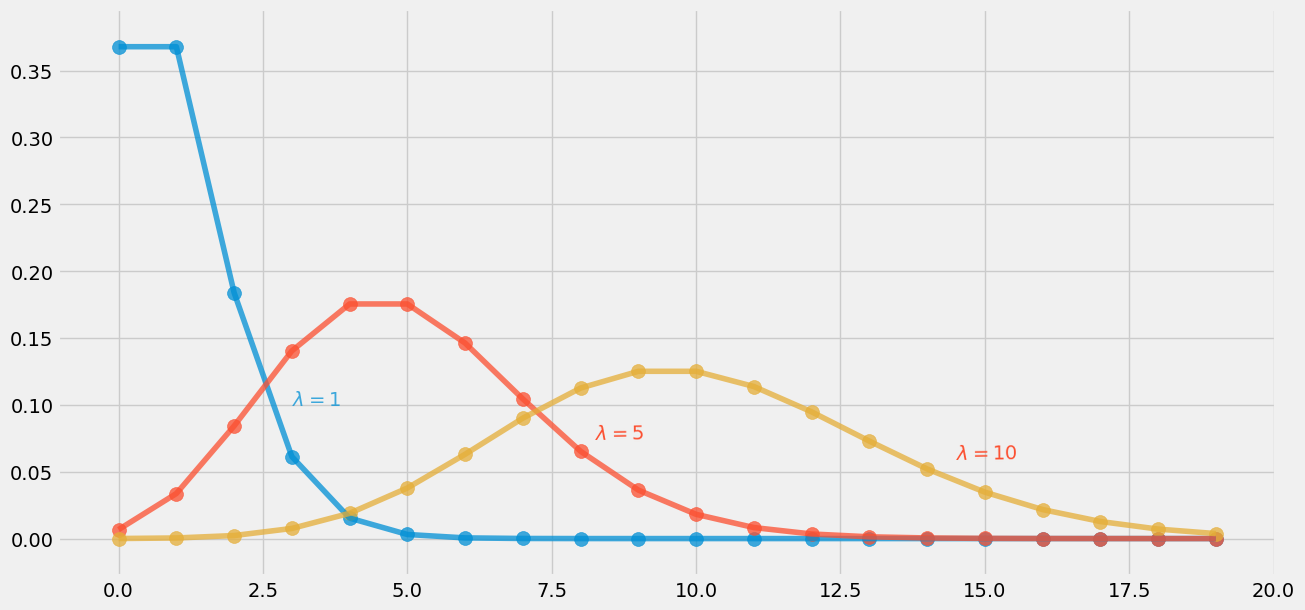
image.png

λ对结果的影响

plt.figure(dpi=100)
# PDF λ=1
plt.scatter(np.arange(20), stats.poisson.pmf(np.arange(20), mu=1), alpha=0.75, s=100)
plt.plot(np.arange(20), stats.poisson.pmf(np.arange(20), mu=1), alpha=0.75)

#PDF λ=5
plt.scatter(np.arange(20), stats.poisson.pmf(np.arange(20), mu=5), alpha=0.75, s=100)
plt.plot(np.arange(20), stats.poisson.pmf(np.arange(20), mu=5), alpha=0.75)

#PDF λ=10
plt.scatter(np.arange(20), stats.poisson.pmf(np.arange(20), mu=10), alpha=0.75, s=100)
plt.plot(np.arange(20), stats.poisson.pmf(np.arange(20), mu=10), alpha=0.75)

#LEGEND 图例
plt.text(x=3, y=0.1, s="$λ=1$", alpha=0.75, weight="bold", color="#008fd5")
plt.text(x=8.25, y=0.075, s="$λ=5$", rotation=0.75, weight="bold", color="#fc4f30")
plt.text(x=14.5, y=0.06, s="$λ=10$", rotation=0.75, weight="bold", color="#fc4f30")
plt.show()

image.png

# 绘制PDF
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize']=(14,7)

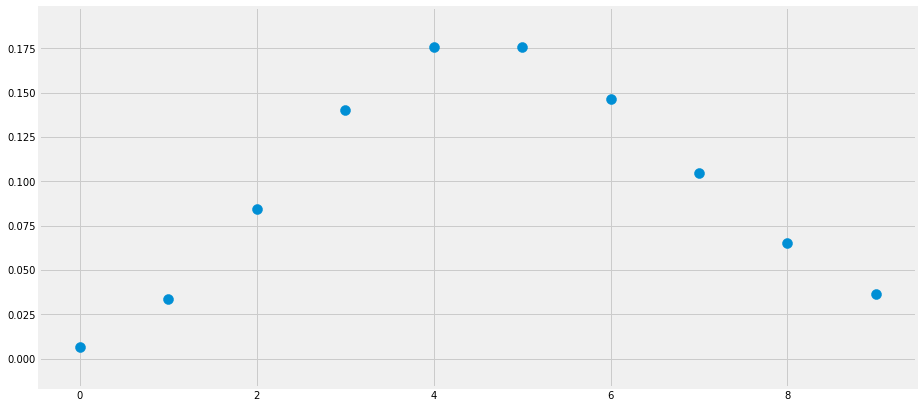
# 绘制泊松分布的PMF曲线
x_s = np.arange(10)
y_s = stats.poisson.pmf(k=x_s, mu=5)
plt.scatter(x_s, y_s, s=100)
plt.show()

image.png

# 统计累积概率
# CDF
from scipy.stats import poisson

# 求事件发生次数小于3的概率
print("p(x<3)={}".format(poisson.cdf(k=3,mu=5)))

# 求事件发生次数大于2小于8的概率
print("p(2<x<8)={}".format(poisson.cdf(k=8,mu=5)-poisson.cdf(k=2,mu=5)))

# p(x<3)=0.2650259152973616
# p(2<x<8)=0.8072543457950705

0xFF 总结

四、概率分布 - 图29