0x00 数据集的拆分

在这篇文章中，我们使用训练数据集和测试数据集来判断模型的好坏，给出并实现accurcay这一分类问题常用指标。最后我们再探寻超参数的选择对模型的影响。

一、训练数据集&测试数据集

我们已经兴致勃勃的训练好了一个模型了，问题是：它能直接拿到生产环境正确使用么？

我们现在只是能拿到一个预测结果，还不知道这个模型效果怎么样？
预测的结果准不准
如果拿到真实环境，其实是没有label的，我们怎么对结果进行验证呢？

实际上，从训练好模型到真实使用，还差着远呢。我们要做的第一步就是：

将原始数据中的一部分作为训练数据、另一部分作为测试数据。使用训练数据训练模型，再用测试数据看好坏。即通过测试数据判断模型好坏，然后再不断对模型进行修改。

1.鸢尾花train_test

鸢尾花数据集是UCI数据库中常用数据集。我们可以直接加载数据集，并尝试对数据进行一定探索：

import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
iris = datasets.load_iris()
X = iris.data
y = iris.target
X.shape  # (150, 4)
y.shape  # (150,)

2. 拆分数据集

进行训练数据集、测试数据集的拆分工作（train_test_split）一般情况下我们按照0.8:0.2的比例进行拆分，但是有时候我们不能简单地把前n个数据作为训练数据集，后n个作为测试数据集。如果数据是有顺序的，我们可以将数据集打乱，做一个shuffle操作。但是本数据集的特征和标签是分开的，也就是说我们分别乱序后，原来的对应关系就不存在了。有两种方法解决这一问题：

将X和y合并为同一个矩阵，然后对矩阵进行shuffle，之后再分解
对y的索引进行乱序，根据索引确定与X的对应关系，最后再通过乱序的索引进行赋值

# 方式一
# 使用concatenate函数进行拼接, 因为传入的矩阵必须具有相同的形状; 因此需要对label进行reshape操作, 
# reshape(-1,1)表示行数自动计算,1列 axis=1表示纵向拼接
tempConcat = np.concatenate((X, y.reshape(-1,1)), axis=1)  
# 拼接好后，直接进行乱序操作
np.random.shuffle(tempConcat)  
# 再将shuffle后的数组使用split方法拆分
shuffle_X,shuffle_y = np.split(tempConcat, [4], axis=1)  
# 设置划分的比例
test_ratio = 0.2
test_size = int(len(X) * test_ratio)
X_train = shuffle_X[test_size:]
y_train = shuffle_y[test_size:]
X_test = shuffle_X[:test_size]
y_test = shuffle_y[:test_size]
print(X_train.shape)  # (120, 4)
print(X_test.shape)  # (30, 4)
print(y_train.shape)  # (120, 1)
print(y_test.shape)  # (30, 1)

# 方式二
# 将x长度这么多的数, 返回一个新的打乱顺序的数组; 注意, 数组中的元素不是原来的数据, 而是混乱的索引
shuffle_index = np.random.permutation(len(X))
# 指定测试数据的比例
test_ratio = 0.2
test_size = int(len(X) * test_ratio)
test_index = shuffle_index[:test_size]
train_index = shuffle_index[test_size:]
X_train = X[train_index]
X_test = X[test_index]
y_train = y[train_index]
y_test = y[test_index]
print(X_train.shape)  # (120, 4)
print(X_test.shape)  # (30, 4)
print(y_train.shape)  # (120,)
print(y_test.shape)  # (30,)

3. 编写自己的train_test_split

下面编写自己的train_test_split，并封装成方法。

编写一个自己的train_test_split方法。这个方法可以放到model_selection.py下。因为分割训练集和测试集合，可以帮助我们测试机器学习性能，能够帮助我们更好地选择模型。

import numpy as np


def train_test_split(X, y, test_ratio=0.2, seed=None):
    """
    将矩阵X和标签y按照test_ration分割成
        X_train
        X_test
        y_train
        y_test
    """
    assert X.shape[0] == y.shape[0],    "the size of X must be equal to the size of y"
    assert 0.0 <= test_ratio <= 1.0,    "test_train must be valid"

    if seed:   # 是否使用随机种子, 使随机结果相同, 方便debug
        np.random.seed(seed)
    shuffle_index = np.random.permutation(len(X))  # permutation(n) 可直接生成一个随机排列的数组, 含有n个元素

    test_size = int(len(X) * test_ratio)
    test_index = shuffle_index[:test_size]
    train_index = shuffle_index[test_size:]
    X_train = X[train_index]
    X_test = X[test_index]
    y_train = y[train_index]
    y_test = y[test_index]
    return X_train, X_test, y_train, y_test

调用

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from MachineLearning.ML_Algorithms.my_score import accuracy_score


# 手写数字数据集，封装好的对象，可以理解为一个字段
digits = datasets.load_digits()
# 可以使用keys()方法来看一下数据集的详情
dig_inf = digits.keys()
print(dig_inf)

# sklearn.datasets提供的数据描述
print(digits.DESCR)


X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y)

print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

再得到分割好的训练数据集和测试数据集以后，下面将其应用于kNN算法中。

我们可以简单验证一下，X_train, y_train通过fit传入算法，然后对X_test做预测，得到y_predict。

然后我们可以直观地把y_predict和实际的结果y_test进行一个比较，看有多少个元素一样。当然我们也可以自己计算一下正确率

from MachineLearning.ML_Algorithms.model_selection import train_test_split
from sklearn import datasets


iris = datasets.load_iris()

X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)

print(X_train.shape)  # (120, 4)
print(X_test.shape)  # (30, 4)
print(y_train.shape)  # (120,)
print(y_test.shape)  # (30,)


# 使用我们封装的kNN算法
from MachineLearning.ML_Algorithms.kNN import kNNClassifier

my_kNNClassifier = kNNClassifier(k=3)
my_kNNClassifier.fit(X_train, y_train)  # kNN(k=3)

y_predict = my_kNNClassifier.predict(X_test)
print(y_predict)  # array([1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 2, 1, 0, 2, 1, 1, 2, 0, 0, 1, 1, 2, 1, 0, 2, 1, 0, 0, 1, 0])
print(y_test)  # array([1, 1, 2, 1, 1, 1, 2, 1, 2, 1, 2, 1, 0, 2, 1, 1, 2, 0, 0, 1, 1, 2, 1, 0, 2, 1, 0, 0, 1, 0])
# 两个向量的比较，返回一个布尔型向量，对这个布尔向量（faluse=1，true=0）sum求和
print(sum(y_predict == y_test))  # 29
print(sum(y_predict == y_test)/len(y_test))  # 0.9666666666666667

4. sklearn中的train_test_split

# 使用sklearn中的train_test_split
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)

print(X_train.shape)  # (120, 4)
print(X_test.shape)  # (30, 4)
print(y_train.shape)  # (120,)
print(y_test.shape)  # (30,)

from sklearn.neighbors import KNeighborsClassifier


kNN_classifier = KNeighborsClassifier(n_neighbors=6)
kNN_classifier.fit(X_train, y_train)
# KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=6, p=2, weights='uniform')

yy_predict = kNN_classifier.predict(X_test)
yy_predict  # array([2, 0, 2, 1, 0, 2, 2, 2, 0, 0, 0, 1, 2, 1, 2, 2, 0, 2, 1, 0, 2, 1, 2, 0, 2, 2, 0, 1, 2, 2])

sum(yy_predict == y_test)  # 30
sum(yy_predict == y_test) / len(y_test)  # 1

二、分类准确度accuracy

在划分出测试数据集后，我们就可以验证其模型准确率了。在这了引出一个非常简单且常用的概念：accuracy（分类准确度）

accuracy_score：函数计算分类准确率，返回被正确分类的样本比例（default）或者是数量（normalize=False）在多标签分类问题中，该函数返回子集的准确率，对于一个给定的多标签样本，如果预测得到的标签集合与该样本真正的标签集合严格吻合，则subset accuracy =1.0否则是0.0

因accuracy定义清洗、计算方法简单，因此经常被使用。但是它在某些情况下并不一定是评估模型的最佳工具。精度（查准率）和召回率（查全率）等指标对衡量机器学习的模型性能在某些场合下要比accuracy更好。

当然这些指标在后续都会介绍。在这里我们就使用分类精准度，并将其作用于一个新的手写数字识别分类算法上。

1. 数据探索

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier


# 手写数字数据集，封装好的对象，可以理解为一个字段
digits = datasets.load_digits()
# 可以使用keys()方法来看一下数据集的详情
digits.keys()  # dict_keys(['data', 'target', 'target_names', 'images', 'DESCR'])

我们可以看一下sklearn.datasets提供的数据描述(print(digits.DESCR))：

5620张图片, 每张图片有64个像素点即特征(8*8整数像素图像), 每个特征的取值范围是1～16(sklearn中的不全), 对应的分类结果是10个数字

import matplotlib.pyplot as plt


X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y)

print(X_train.shape)  # (1347, 64)
print(X_test.shape)  # (450, 64)
print(y_train.shape)  # (1347,)
print(y_test.shape)  # (450,)

# 特征的
shapeX = digits.data
X.shape  # (1797, 64)

# 标签的
shapey = digits.target
y.shape  # (1797,)

# 标签分类
digits.target_names  # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# 去除某一个具体的数据，查看其特征以及标签信息
some_digit = X[666]
some_digit
# array([ 0.,  0.,  5., 15., 14.,  3.,  0.,  0.,  0.,  0., 13., 15.,  9.,
#        15.,  2.,  0.,  0.,  4., 16., 12.,  0., 10.,  6.,  0.,  0.,  8.,
#        16.,  9.,  0.,  8., 10.,  0.,  0.,  7., 15.,  5.,  0., 12., 11.,
#         0.,  0.,  7., 13.,  0.,  5., 16.,  6.,  0.,  0.,  0., 16., 12.,
#        15., 13.,  1.,  0.,  0.,  0.,  6., 16., 12.,  2.,  0.,  0.])

y[666]  # 0

# 也可以这条数据进行可视化
import matplotlib.pyplot as plt

some_digmit_image = some_digit.reshape(8, 8)
plt.imshow(some_digmit_image, cmap = matplotlib.cm.binary)
plt.show()

结果展示如下: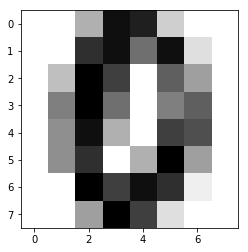
下载.png

2. 在分类任务结束后，我们就可以计算分类算法的准确率

import numpy as np


def accuracy_score(y_true, y_predict):
    """计算y_true和y_predict之间的准确率"""

    assert y_true.shape[0] == y_predict.shape[0], "the size of y_true must be equal to the size of y_predict"

    return sum(y_true == y_predict) / len(y_true)

from playML.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_ratio=0.2)

print(X_train.shape)  # (1347, 64)
print(X_test.shape)  # (450, 64)
print(y_train.shape)  # (1347,)
print(y_test.shape)  # (450,)


# 使用我们自己封装的函数
from playML.kNN import kNNClassifier
my_knn_clf= kNNClassifier(k=3)
my_knn_clf.fit(X_train, y_train)  # kNN(k=3)
y_predict = my_knn_clf.predict(X_test)
y_predict

sum(y_predict == y_test) / len(y_test)  # 0.9916434540389972


from playML.metrics import accuracy_score

accuracy_score(y_test, y_predict)  # 0.9916434540389972
my_knn_clf.score(X_test, y_test)  # 0.9916434540389972

3. 使用sklearn中的准确度

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)


from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier(n_neighbors=3)

knn_clf.fit(X_train, y_train)  
# KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=3, p=2, weights='uniform')
yy_predict = knn_clf.predict(X_test)


from sklearn.metrics import accuracy_score

accuracy_score(y_test, yy_predict)  # 0.9888888888888889
knn_clf.score(X_test, y_test)  # 0.9888888888888889

三、超参数

1. 超参数简介

之前我们都是为knn算法传一个默认的k值。在具体使用时应该传递什么值合适呢？这就涉及了机器学习领域中的一个重要问题：超参数。

所谓超参数，就是在机器学习算法模型执行之前需要指定的参数。（调参调的就是超参数）如kNN算法中的k。
与之相对的概念是模型参数，即算法过程中学习的属于这个模型的参数（kNN中没有模型参数，回归算法有很多模型参数）

如何选择最佳的超参数，这是机器学习中的一个永恒的问题。在实际业务场景中，调参的难度大很多，一般我们会业务领域知识、经验数值、实验搜索等方面获得最佳参数。

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()  # 加载手写数字数据集
X = digits.data
y = digits.target


from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)


from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test, y_test)  # 0.9888888888888889

2. 寻找最好的k

针对于上一小节的手写数字识别分类代码，尝试寻找最好的k值。逻辑非常简单，就是设定一个初始化的分数，然后循环更新k值，找到最好的score

best_score = 0.0
best_k = -1
for k in range(1, 11):
    knn_clf = KNeighborsClassifier(n_neighbors=k)
    knn_clf.fit(X_train, y_train)
    score = knn_clf.score(X_test, y_test)
    if score > best_score:
        best_k = k
        best_score = score

print("best_k =", best_k)  # best_k = 4
print("best_score =", best_score)  # best_score = 0.9916666666666667

可以看到，最好的k值是4，在我们设定的k的取值范围中间。需要注意的是，如果我们得到的值正好在边界上，我们需要稍微扩展一下取值范围。

3. 另一个超参数：权重

在回顾kNN算法思想时，我们应该还记得，对于简单的kNN算法，只需要考虑最近的n个数据是什么即可。但是如果我们考虑距离呢？
如果我们认为，距离样本数据点最近的节点，对其影响最大，那么我们使用距离的倒数作为权重。假设距离样本点最近的三个节点分别是红色、蓝色、蓝色，距离分别是1、4、3。那么普通的k近邻算法：蓝色获胜。考虑权重（距离的倒数）：红色：1，蓝色：1/3 + 1/4 = 7/12，红色胜。
在 sklearn.neighbors 的构造函数 KNeighborsClassifier 中有一个参数：weights，默认是uniform即不考虑距离，也可以写distance来考虑距离权重(默认是欧拉距离，如果要是曼哈顿距离，则可以写参数p（明可夫斯基距离的参数），这个也是超参数)
因为有两个超参数，因此使用双重循环，去查找最合适的两个参数，并打印。

best_score = 0.0
best_k = -1
best_method = ""
for method in ["uniform", "distance"]:
    for k in range(1, 11):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k = k
            best_score = score
            best_method = method

print("best_method =", best_method)
print("best_k =", best_k)
print("best_score =", best_score)
# best_method = uniform
# best_k = 4
# best_score = 0.9916666666666667

sk_knn_clf = KNeighborsClassifier(n_neighbors=4, weights="distance", p=1)
sk_knn_clf.fit(X_train, y_train)
sk_knn_clf.score(X_test, y_test)  # 0.9833333333333333

搜索明可夫斯基距离相应的p

best_score = 0.0
best_k = -1
best_p = -1

for k in range(1, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights="distance", p=p)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k = k
            best_p = p
            best_score = score

print("best_k =", best_k)
print("best_p =", best_p)
print("best_score =", best_score)
# best_k = 3
# best_p = 2
# best_score = 0.9888888888888889

4. 超参数网格搜索

在具体的超参数搜索过程中会需要很多问题，超参数过多、超参数之间相互依赖等等。如何一次性地把我们想要得到最好的超参数组合列出来。sklearn中专门封装了一个超参数网格搜索方法Grid Serach。
在进行网格搜索之前，首先需要定义一个搜索的参数param_search。是一个数组，数组中的每个元素是个字典，字典中的是对应的一组网格搜索，每一组网格搜索是这一组网格搜索每个参数的取值范围。键是参数的名称，值是键所对应的参数的列表。

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()  # 加载手写数字数据集
X = digits.data
y = digits.target


from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)


from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier(n_neighbors=4, weights="uniform")
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test, y_test)  # 0.9916666666666667

param_grid = [
    {
        'weights': ['uniform'], 
        'n_neighbors': [i for i in range(1, 11)]
    },
    {
        'weights': ['distance'],
        'n_neighbors': [i for i in range(1, 11)], 
        'p': [i for i in range(1, 6)]
    }
]

可以看到，当weights = uniform即不使用距离时，我们只搜索超参数k，当weights = distance即使用距离时，需要看超参数p使用那个距离公式。
下面创建要进行网格搜索所对应的分类算法并调用网格搜索：

knn_clf = KNeighborsClassifier()  # 

from sklearn.model_selection import GridSearchCV

grid_search = GridSearchCV(knn_clf, param_grid)
%%time
grid_search.fit(X_train, y_train)

grid_search.best_estimator_
# KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=3, p=3, weights='distance')
grid_search.best_score_  # 0.9853862212943633
grid_search.best_params_  # {'n_neighbors': 3, 'p': 3, 'weights': 'distance'}

knn_clf = grid_search.best_estimator_
knn_clf.predict(X_test)
knn_clf.score(X_test, y_test)  # 0.9833333333333333

%%time
grid_search = GridSearchCV(knn_clf, param_grid, n_jobs=-1, verbose=2)
# n_jobs使用计算机的核数,-1使用所有核 verbose输出
grid_search.fit(X_train, y_train)

我们会注意到，best_estimator_和best_score_参数后面有一个_。这是一种常见的语法规范，不是用户传入的参数，而是根据用户传入的规则，自己计算出来的结果，参数名字后面接_

Data_Scientist

二、如何评价模型的好坏