五、概率分布实战

二项分布

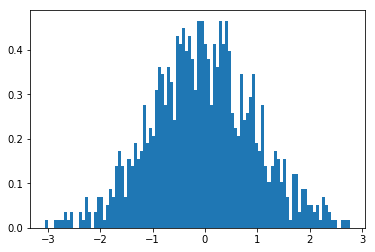
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
num_trials = 60
x = np.arange(num_trials)
plt.plot(x, binom(num_trials, 0.2).pmf(x), 'o-', label='p=0.2')
plt.plot(x, binom(num_trials, 0.5).pmf(x), 'o-', label='p=0.5')
plt.plot(x, binom(num_trials, 0.7).pmf(x), 'o-', label='p=0.7')
plt.legend(shadow=True)
plt.title('二项分布：p对结果的影响')
plt.show()
print('当p不同时，成功m次的能性的最大值都出现在均值处，对应概率为n*p')

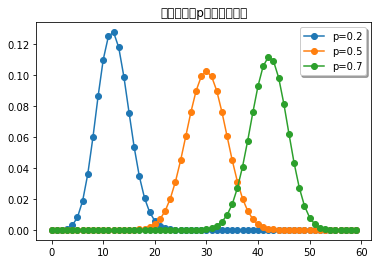
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
n1 = 10
n2 = 15
n3 = 20
p = 0.5
x = np.arange( max([n1,n2,n3])+1 )
plt.plot(x, binom.pmf(x, p = 0.5, n = n1), 'o-', label='n=10')
plt.plot(x, binom.pmf(x, p = 0.5, n = n2), 'o-', label='n=15')
plt.plot(x, binom.pmf(x, p = 0.5, n = n3), 'o-', label='n=20')
plt.legend(shadow=True)
plt.title('二项分布：n对结果的影响')
plt.show()
print('当N不同时，成功m次的可能性的最大值都出现在均值处，对应概率为n*p')

几何分布

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats


"""
第1步，定义随机变量
首次表白成功的次数，可能是1次，2次，3次等
"""

# 第k次做某件事情，才取到第1次成功
# 这里我们想知道5次表白成功的概率
k = 5   
# 做某件事情成功的概率，这里假设每次表白成功概率都是60%
p = 0.6 
X = np.arange(1, k+1, 1)

"""
第2步 求对应分布的概率: 概率质量函数 (PMF)
它返回一个列表，列表中每个元素表示随机变量中对应值的概率
分别表示表白第1次才成功的概率，表白第2次才成功的概率，表白第3次才成功的概率，表白第4次才成功的概率，表白第5次才成功的概率
"""

pList = stats.geom.pmf(X, p)

# 第3步，绘图
plt.plot(X, pList, marker='o', linestyle='None')
plt.vlines(X, 0, pList)
# x轴文本
plt.xlabel('随机变量: 表白第k次才首次成功')
# y轴文本
plt.ylabel('概率')
#标题
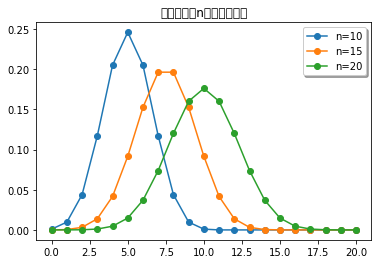
plt.title('几何分布：p=%.2f' % p)
#显示图形
plt.show()

泊松分布

from scipy import stats

mu=2
k=4
X=np.arange(0, k+1, 1)
plist=stats.geom.pmf(X, p)
plt.plot(X, plist, marker='o', linestyle='None')
plt.vlines(X, 0, plist)
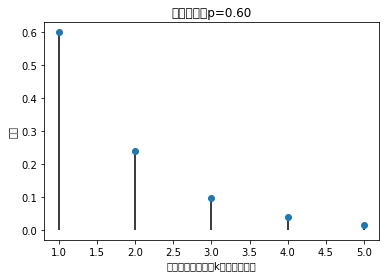
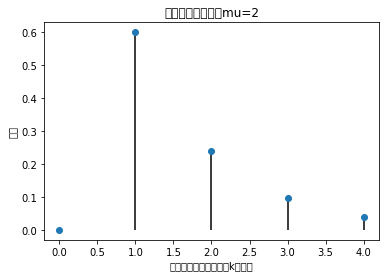
plt.xlabel('随机变量: 某路口发生k次事故')
plt.ylabel('概率')
plt.title('泊松分布: 平均值mu=%i' % mu)
plt.show()

正态分布

import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt


def demo1():
  mu, sigma = 0, 1
  sampleNo = 1000
  np.random.seed(0)
  s = np.random.normal(mu, sigma, sampleNo)

  plt.hist(s, bins=100, normed=True)
  plt.show()