0x01 数据归一化

1.1 为什么要数据归一化

在实际应用中，样本的不同特征的单位不同，会在求距离时造成很大的影响。比如：在两个样本中肿瘤大小的分别为1cm和5cm，发现时间分别为100天和200天，那么在求距离时，时间差为100、大小差为4，那么其结果会被时间所主导，因为肿瘤大小的差距太小了。但是如果我们把时间用年做单位，0.27年与0.55年的差距又远小于肿瘤大小的差距，结果又会被大小主导了。
我们发现，在量纲不同的情况下，以上的情况，不能反映样本中每一个特征的重要程度。这就需要数据归一化了。
一般来说，我们的解决方案是：把所有的数据都映射到同一个尺度（量纲）上。
常用的数据归一化有两种：

  • 最值归一化(normalization)： 把所有数据映射到0-1之间。最值归一化的使用范围是特征的分布具有明显边界的(分数0～100分、灰度0～255)，受outlier的影响比较大

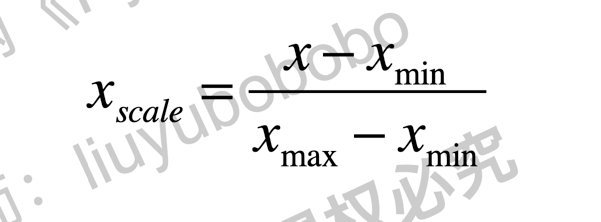
image.png

  • 均值方差归一化(standardization)： 把所有数据归一到均值为0方差为1的分布中。适用于数据中没有明显的边界，有可能存在极端数据值的情况.

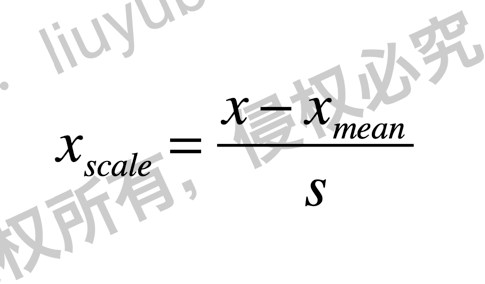
image.png

1.2 最值归一化实现

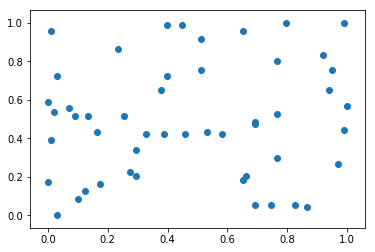
  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. x = np.random.randint(0, 100, 100) 
  6. # 最值归一化（向量）
  7. # 最值归一化公式，映射到0，1之间
  8. (x - np.min(x)) / (np.max(x) - np.min(x))
  10. # 最值归一化（矩阵）
  11. # 0～100范围内的50*2的矩阵
  12. X = np.random.randint(0, 100, (50, 2))
  13. X = np.array(X, dtype=float)  # 将矩阵改为浮点型
  14. # 最值归一化公式，对于每一个维度（列方向）进行归一化。
  15. # X[:,0]第一列，第一个特征
  16. X[:, 0] = (X[:, 0] - np.min(X[:, 0])) / (np.max(X[:, 0]) - np.min(X[:, 0]))
  17. # X[:,1]第一列，第二个特征
  18. X[:, 1] = (X[:, 1] - np.min(X[:, 1])) / (np.max(X[:, 1]) - np.min(X[:, 1]))
  20. ”“”
  21. # 如果有n个特征，可以写个循环：
  22. for i in range(0, n):
  23.     X[:,i] = (X[:,i]-np.min(X[:,i])) / (np.max(X[:,i] - np.min(X[:,i])))
  24. “”“
  26. np.mean(X[:, 0])  # 0.4716326530612245
  27. np.std(X[:, 0])  # 0.3248636660191091
  28. np.mean(X[:, 1])  # 0.4942268041237113
  29. np.std(X[:, 1])  # 0.2936853396994547
  30. plt.scatter(X[:,0], X[:,1])
  31. plt.show()

image.png

1.3 均值方差归一化实现

  1. X2 = np.random.randint(0, 100, (50, 2))
  3. X2 = np.array(X2, dtype=float)
  5. ”“”
  6. # 方式一: 直接对每一列做均值方差归一化
  7. X2[:,0] = (X2[:,0] - np.mean(X2[:,0])) / np.std(X2[:,0])
  8. X2[:,1] = (X2[:,1] - np.mean(X2[:,1])) / np.std(X2[:,1])
  9. “”“
  11. # 方式二: 套用公式，对每一列做均值方差归一化
  12. for i in range(0,2):
  13.     X2[:,i]=(X2[:,i]-np.mean(X2[:,i])) / np.std(X2[:,i])
  15. np.mean(X2[:,0])  # -9.769962616701378e-17
  16. np.std(X2[:,0])  # 0.9999999999999999
  17. np.mean(X2[:,1])  # 7.993605777301127e-17
  18. np.std(X2[:,1])  # 1.0
  20. plt.scatter(X2[:,0], X2[:,1])
  21. plt.show()

image.png

1.4 Scikit-learn中的Scaler

首先我们来看一个在实际使用归一化时的一个小陷阱。
我们在建模时要将数据集划分为训练数据集&测试数据集。
训练数据集进行归一化处理，需要计算出训练数据集的均值mean_train和方差std_train。

问题是：我们在对测试数据集进行归一化时，要计算测试数据的均值和方差么？
答案是否定的。在对测试数据集进行归一化时，仍然要使用训练数据集的均值train_mean和方差std_train。这是因为测试数据是模拟的真实环境，真实环境中可能无法得到均值和方差，对数据进行归一化。只能够使用公式(x_test - mean_train) / std_train并且，数据归一化也是算法的一部分，针对后面所有的数据，也应该做同样的处理.
因此我们要保存训练数据集中得到的均值和方差。

在sklearn中专门的用来数据归一化的方法：StandardScaler。

  1. import numpy as np
  2. from sklearn import datasets
  4. iris = datasets.load_iris()
  5. X = iris.data
  6. y = iris.target
  8. from sklearn.model_selection import train_test_split
  9. X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=666)
  11. X[:10,:]
# X[:10,:]
array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],
[5. , 3.6, 1.4, 0.2],
[5.4, 3.9, 1.7, 0.4],
[4.6, 3.4, 1.4, 0.3],
[5. , 3.4, 1.5, 0.2],
[4.4, 2.9, 1.4, 0.2],
[4.9, 3.1, 1.5, 0.1]])		 
  1. # scikit-learn中的StandardScaler
  3. standardScaler = StandardScaler()
  4. standardScaler.fit(X_train)  # StandardScaler(copy=True, with_mean=True, with_std=True)
  5. standardScaler.mean_  # array([5.83416667, 3.08666667, 3.70833333, 1.17      ])
  6. standardScaler.scale_  # array([0.81019502, 0.44327067, 1.76401924, 0.75317107])
  8. standardScaler.transform(X_train) 
  9. X_train[:10,:]
  10. array([[5.1, 3.5, 1.4, 0.2],
  11.        [4.9, 3. , 1.4, 0.2],
  12.        [5.7, 2.8, 4.1, 1.3],
  13.        [6.2, 3.4, 5.4, 2.3],
  14.        [5.1, 2.5, 3. , 1.1],
  15.        [7. , 3.2, 4.7, 1.4],
  16.        [6.1, 2.6, 5.6, 1.4],
  17.        [7.6, 3. , 6.6, 2.1],
  18.        [5.2, 4.1, 1.5, 0.1],
  19.        [6.2, 2.2, 4.5, 1.5]])
  20. X_train = standardScaler.transform(X_train)
  21. X_train[:10,:]
  22. array([[-0.90616043,  0.93246262, -1.30856471, -1.28788802],
  23.        [-1.15301457, -0.19551636, -1.30856471, -1.28788802],
  24.        [-0.16559799, -0.64670795,  0.22203084,  0.17260355],
  25.        [ 0.45153738,  0.70686683,  0.95898425,  1.50032315],
  26.        [-0.90616043, -1.32349533, -0.40154513, -0.09294037],
  27.        [ 1.43895396,  0.25567524,  0.56216318,  0.30537551],
  28.        [ 0.3281103 , -1.09789954,  1.0723617 ,  0.30537551],
  29.        [ 2.1795164 , -0.19551636,  1.63924894,  1.23477923],
  30.        [-0.78273335,  2.2860374 , -1.25187599, -1.42065998],
  31.        [ 0.45153738, -2.00028272,  0.44878573,  0.43814747]])
  33. X_test_standard = standardScaler.transform(X_test)
# 使用归一化后的数据进行knn分类

from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train, y_train)
# KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=3, p=2, weights='uniform')

knn_clf.score(X_test_standard, y_test)  # 归一化后的测试数据
# 1.0

knn_clf.score(X_test, y_test)  # 注意，此时不能传入没有归一化的数据！
# 0.3333333333333333

1.5 自己实现均值方差归一化

import numpy as np


class StandardScaler:

    def __init__(self):
        self.mean_ = None
        self.scale_ = None

    def fit(self, X):
        """根据训练数据集X获得数据的均值和方差"""
        assert X.ndim == 2, "The dimension of X must be 2"

        self.mean_ = np.array([np.mean(X[:, i]) for i in range(X.shape[1])])
        self.scale_ = np.array([np.std(X[:, i]) for i in range(X.shape[1])])

        return self

    def transform(self, X):
        """将X根据这个StandardScaler进行均值方差归一化处理"""
        assert X.ndim == 2, "The dimension of X must be 2"
        assert self.mean_ is not None and self.scale_ is not None, "must fit before transform"
        assert X.shape[1] == len(self.mean_), "the feature number of X must be equal to mean_ and std_"

        resX = np.empty(shape=X.shape, dtype=float)
        for col in range(X.shape[1]):
            resX[:, col] = (X[:, col] - self.mean_[col]) / self.scale_[col]
        return resX

X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=666)


from playML.preprocessing import StandardScaler

my_standardScalar = StandardScaler() 
my_standardScalar.fit(X_train)  # <playML.preprocessing.StandardScaler at 0x1286ae438>

my_standardScalar.mean_  # array([5.83416667, 3.08666667, 3.70833333, 1.17      ])
my_standardScalar.scale_  # array([0.81019502, 0.44327067, 1.76401924, 0.75317107])

X_train = my_standardScalar.transform(X_train)
X_train[:10,:]
array([[-0.90616043,  0.93246262, -1.30856471, -1.28788802],
       [-1.15301457, -0.19551636, -1.30856471, -1.28788802],
       [-0.16559799, -0.64670795,  0.22203084,  0.17260355],
       [ 0.45153738,  0.70686683,  0.95898425,  1.50032315],
       [-0.90616043, -1.32349533, -0.40154513, -0.09294037],
       [ 1.43895396,  0.25567524,  0.56216318,  0.30537551],
       [ 0.3281103 , -1.09789954,  1.0723617 ,  0.30537551],
       [ 2.1795164 , -0.19551636,  1.63924894,  1.23477923],
       [-0.78273335,  2.2860374 , -1.25187599, -1.42065998],
       [ 0.45153738, -2.00028272,  0.44878573,  0.43814747]])

X_test_standard = standardScaler.transform(X_test)
X_test_standard[:10,:]
array([[-0.28902506, -0.19551636,  0.44878573,  0.43814747],
       [-0.04217092, -0.64670795,  0.78891808,  1.63309511],
       [-1.0295875 , -1.77468693, -0.23147896, -0.22571233],
       [-0.04217092, -0.87230374,  0.78891808,  0.96923531],
       [-1.52329579,  0.03007944, -1.25187599, -1.28788802],
       [-0.41245214, -1.32349533,  0.16534211,  0.17260355],
       [-0.16559799, -0.64670795,  0.44878573,  0.17260355],
       [ 0.82181859, -0.19551636,  0.8456068 ,  1.10200727],
       [ 0.57496445, -1.77468693,  0.39209701,  0.17260355],
       [-0.41245214, -1.09789954,  0.39209701,  0.03983159]])

0x02 KNN的优缺点

KNN的主要优点有：

  1. 理论成熟，思想简单，既可以用来做分类也可以用来做回归
  2. 天然解决多分类问题，也可用于回归问题
  3. 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感
  4. 由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合

KNN的主要缺点有：

  1. 计算量大，效率低。即使优化算法，效率也不高。
  2. 高度数据相关，样本不平衡的时候，对稀有类别的预测准确率低
  3. 相比决策树模型，KNN模型可解释性不强
  4. 维度灾难：随着维度的增加，“看似相近”的两个点之间的距离越来越大，而knn非常依赖距离
维数 点到点 距离
1维 0到1的距离 1
2维 (0,0)到(1,1)的距离 1.414
3维 (0,0,0)到(1,1,1)的距离 1.73
64维 (0,0,…0)到(1,1,…1) 8
10000维 (0,0,…0)到(1,1,…1) 100

大家感觉一万维貌似很多，但实际上就是100*100像素的黑白灰图片。