0x00 KNN算法概述
KNN(kNN,k-NearestNeighbor)算法中文名称叫做K近邻算法,是众多机器学习算法里面最基础入门的算法。所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。它是一个有监督的机器学习算法,既可以用来做分类任务也可以用来做回归任务。KNN算法的核心思想是未标记的样本的类别,由距离他最近的K个邻居投票来决定。
KNN是一种分类(classification)算法,它输入基于实例的学习(instance-based learning),属于懒惰学习(lazy learning)即KNN没有显式的学习过程,也就是说没有训练阶段,数据集事先已有了分类和特征值,待收到新样本后直接进行处理。与急切学习(eager learning)相对应。
KNN是通过测量不同特征值之间的距离进行分类。
思路是:如果一个样本在特征空间中的k个最邻近的样本中的大多数属于某一个类别,则该样本也划分为这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
算法的描述:
- 计算测试数据与各个训练数据之间的距离
- 按照距离的递增关系进行排序
- 选取距离最小的k个点
- 确定前k个点所在类别的出现频率
- 返回前K个点中出现频率最高的类别作为测试数据的预测分类
0x01 关于K的取值
K: 近邻数. 即在预测目标点时取几个邻近的点来预测
K值的选取非常重要, 因为:
- 如果当k取值过小时, 一旦有噪声得成分存在将会对预测产生比较大影响, 例如取K值为1时, 一旦最近的一个点是噪声, 那么就会出现偏差, K值的减小意味着整体模型变得复杂, 容易发生过拟合。
- 如果K的值取的过大时, 就相当于用较大邻近域中的训练实例进行预测, 学习的近似误差会增大。这时与输入目标点较远实例也会对预测其作用, 是预测发生错误; K值的增大意味着整体的模型变得简单。
- 如果K==N的时候, 那么就是取全部的实例, 即为取实例中某分类下最多的点,就对预测没有什么实际的意义了
- K的取值尽量要取奇数, 以保证在计算结果最后会产生一个较多的类别; 如果取偶数可能会产生相等的情况,不利于预测。
K的取法
常用的方法是从K=1开始, 使用检验集估计分类器的误差率; 重复该过程, 每次K增值1, 允许增加一个邻近; 选取产生最小误差率的K。一般K不超过20, 上限是n开发, 随着数据集的增大, K的值也要增大
0x02 距离的选取
距离就是平面上两个点的直线距离, 常用的度量方法
- 欧几里得距离
- 余弦值(cos)
- 相关度(correlation)
- 曼哈顿距离(Manhattan distance)
0x03 算法的实现步骤
假设X_test为待标记的样本,X_train为已标记的样本数据集:
- 遍历X_train中的所有样本,计算每个样本与X_test的之间的距离(一般为欧式距离)。并且把距离保存在一个distince 的数组中。
- 对distince数组进行排序,取距离最近的K个点。记作X_knn。
- 在X_knn中统计每个类别的个数,既class_0在X_knn中有几个样本,class_1在X_knn中有几个样本等。
- 待标记样本的类别就是X_knn中样本个数最多的那个类别。
from sklearn import datasetsfrom collections import Counterfrom sklearn.model_selection import train_test_splitimport numpy as np# 导入iris数据iris = datasets.load_iris()X = iris.dataY = iris.targetX_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=20)def euc_dis(instance1, instance2):"""计算两个样本instance1和instance2之间的欧式距离instance1: 第一个样本, array型instance2: 第二个样本, array型"""dist = np.sqrt(sum((instance1 - instance2) ** 2))return distdef knn_classify(X, Y, testInstance, K):"""给定一个测试数据testInstance, 通过KNN算法来预测它的标签。X: 训练数据的特征Y: 训练数据的标签testInstance: 测试数据,这里假定一个测试数据 array型K: 选择多少个neighbors?"""# TODO 返回testInstance的预测标签 = {0,1,2}distances = [euc_dis(x, testInstance) for x in X]kneighbors = np.argsort(distances)[:K]count = Counter(Y[kneighbors])return count.most_common()[0][0]# 预测结果predictions = [knn_classify(X_train, Y_train, data, 3) for data in X_test]correct = np.count_nonzero((predictions==Y_test)==True)# accuracy_score(y_test, clf.predict(X_test))print ("Accuracy is: %.3f" %(correct/len(X_test)))
看完了代码的实现以后。我们来思考一下算法的时间复杂度是多少呢?很明显KNN算法的时间复杂度为O(D_N_N)。其中D为维度数,N为样本总数。从时间复杂度上我们可以很清楚的就知道KNN非常不适合高维度的数据集,容易发生维度爆炸的情况。
同时我们也发现了一个问题在关于K的选择上面,我们一般也要选择K的值应该尽量选择为奇数,并且不要是分类结果的偶数倍,否则会出现同票的情况。那么说到这里,关于K的选择?我们到底应该怎么去选择K的大小比较合适呢?答案是交叉验证。交叉验证指的是将训练数据集进一步分成训练数据和验证数据,选择在验证数据里面最好的超参数组合。交叉验证或者通俗一点的说法就是说调参。调参, 参数一般分为模型参数和超级参数。模型参数是需要我们通过不断的调整模型和超参数训练得到的最佳参数。而超级参数则是我们人为手动设定的值。像在KNN中超参数就是K的值。我们可以通过交叉验证的方式,选择一组最好的K值作为模型最终的K值。下图是五折交叉验证:

0x04 KNN需要注意的几个问题
1.大数吞小数
在进行距离计算的时候, 有时候某个特征的数值会特别的大, 那么计算欧式距离的时候, 其他的特征的值的影响就会非常的小被大数给覆盖掉了; 所以我们很有必要进行特征的标准化或者叫做特征的归一化
2.如何处理大数据量
一旦特征或者样本的数目特别的多,KNN的时间复杂度将会非常的高。解决方法是利用KD-Tree这种方式解决时间复杂度的问题,利用KD树可以将时间复杂度降到O(logD_N_N)。D是维度数,N是样本数。但是这样维度很多的话那么时间复杂度还是非常的高,所以可以利用类似哈希算法解决高维空间问题,只不过该算法得到的解是近似解,不是完全解。会损失精确率
3.怎么处理样本的重要性
利用权重值。我们在计算距离的时候可以针对不同的邻居使用不同的权重值,比如距离越近的邻居我们使用的权重值偏大,这个可以指定算法的weights参数来设置
0x05 代码实现
1、基本实现过程
import numpy as np
import matplotlib.pyplot as plt
raw_data_X = [[3.393533211, 2.331273381],
[3.110073483, 1.781539638],
[1.343808831, 3.368360954],
[3.582294042, 4.679179110],
[2.280362439, 2.866990263],
[7.423436942, 4.696522875],
[5.745051997, 3.533989803],
[9.172168622, 2.511101045],
[7.792783481, 3.424088941],
[7.939820817, 0.791637231]
]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)
print(X_train)
print(y_train)
array([[3.39353321, 2.33127338],
[3.11007348, 1.78153964],
[1.34380883, 3.36836095],
[3.58229404, 4.67917911],
[2.28036244, 2.86699026],
[7.42343694, 4.69652288],
[5.745052 , 3.5339898 ],
[9.17216862, 2.51110105],
[7.79278348, 3.42408894],
[7.93982082, 0.79163723]])
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
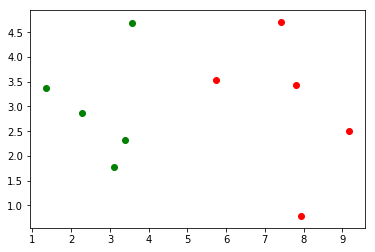
# 绘图
plt.scatter(X_train[y_train==0,0], X_train[y_train==0,1], color='g')
plt.scatter(X_train[y_train==1,0], X_train[y_train==1,1], color='r')
plt.show()
# 目标向量
x = np.array([8.093607318, 3.365731514])
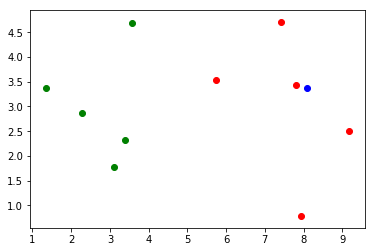
# 对目标向量和训练数据集一起绘图, 查看目标向量所在的坐标位置
plt.scatter(X_train[y_train==0,0], X_train[y_train==0,1], color='g')
plt.scatter(X_train[y_train==1,0], X_train[y_train==1,1], color='r')
plt.scatter(x[0], x[1], color='b')
plt.show()
from math import sqrt
distances = []
for x_train in X_train:
d = sqrt(np.sum((x_train - x)**2))
distances.append(d)
print(distances)
[4.812566907609877,
5.229270827235305,
6.749798999160064,
4.6986266144110695,
5.83460014556857,
1.4900114024329525,
2.354574897431513,
1.3761132675144652,
0.3064319992975,
2.5786840957478887]
np.argsort(distances) # array([8, 7, 5, 6, 9, 3, 0, 1, 4, 2])
nearest = np.argsort(distances)
k = 6
topK_y = [y_train[neighbor] for neighbor in nearest[:k]]
topK_y # [1, 1, 1, 1, 1, 0]
from collections import Counter
votes = Counter(topK_y)
votes # Counter({1: 5, 0: 1})
votes.most_common(1) # [(1, 5)]
predict_y = votes.most_common(1)[0][0]
predict_y # 1
最后预测的结果是目标向量x属于类型1
2、封装函数
可以把我们上面完成的代码封装到一个函数中,以后再有需要预测的数据直接调用函数即可得到预测结果,不需要我们再次实现代码了
import numpy as np
from math import sqrt
from collections import Counter
def kNN_classify(k, X_train, y_train, x): # X_train, y_train 训练数据集, x 目标向量
assert 1 <= k <= X_train.shape[0], "k must be valid"
assert X_train.shape[0] == y_train.shape[0], "the size of X_train must equal to the size of y_train"
assert X_train.shape[1] == x.shape[0], "the feature number of x must be equal to X_train"
# distances = []
# for x_train in X_train:
# d = sqrt(np.sum((x_train - x) ** 2))
# distances.append(d)
distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in X_train]
nearest = np.argsort(distances)
topk_y = [y_train[i] for i in nearest[:k]]
votes = Counter(topk_y)
return votes.most_common(1)[0][0]
准备数据
import numpy as np
import matplotlib.pyplot as plt
raw_data_X = [[3.393533211, 2.331273381],
[3.110073483, 1.781539638],
[1.343808831, 3.368360954],
[3.582294042, 4.679179110],
[2.280362439, 2.866990263],
[7.423436942, 4.696522875],
[5.745051997, 3.533989803],
[9.172168622, 2.511101045],
[7.792783481, 3.424088941],
[7.939820817, 0.791637231]
]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)
x = np.array([8.093607318, 3.365731514])
%run kNN_function/kNN.py # jupyter中调包
predict_y = kNN_classify(6, X_train, y_train, x) # 使用我们封装的kNN_classify函数
predict_y # 1
3、使用scikit-learn中的kNN
from sklearn.neighbors import KNeighborsClassifier
kNN_classifier = KNeighborsClassifier(n_neighbors=6)
kNN_classifier.fit(X_train, y_train) # fit 拟合
kNN_classifier.predict(x.reshape(1, -1)) # predict 预测
# array([1])
X_predict = x.reshape(1, -1)
X_predict
y_predict = kNN_classifier.predict(X_predict)
y_predict[0] # 1
4、重新整理我们的kNN的代码
import numpy as np
from math import sqrt
from collections import Counter
class kNNClassifier:
def __init__(self, k):
"""初始化KNN分类器"""
assert k >= 1, "k must be valid"
self.k = k
self._X_train = None
self._y_train = None
def fit(self, X_train, y_train):
"""根据训练数据集X_train和y_train训练KNN分类器"""
self._X_train = X_train
self._y_train = y_train
return self
def predict(self, X_predict):
"""给定待预测数据集X_predict, 返回表示X_predict的结果向量"""
assert self._X_train is not None and self._y_train is not None, \
"the size of X_train must equal to the size of y_train"
assert X_predict.shape[1] == self._X_train.shape[1], "the feature number of x must be equal to X_train"
y_predict = [self._predict(x) for x in X_predict]
return np.array(y_predict)
def _predict(self, x):
"""给定单个待预测数据x, 返回x的预测结果值"""
assert x.shape[0] == self._X_train.shape[1], "the feature number of x must be equal to X_train"
distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in self._X_train]
nearest = np.argsort(distances)
topk_y = [self._y_train[i] for i in nearest[:self.k]]
votes = Counter(topk_y)
return votes.most_common(1)[0][0]
def __repr__(self):
return "kNN(k=%d)" % self.k
使用我们重新封装的包进行测试和scikit-learn中的kNN得到的结果是一致的
%run kNN/kNN.py
knn_clf = kNNClassifier(k = 6)
knn_clf.fit(X_train, y_train) # kNN(k=6)
y_predict = knn_clf.predict(X_predict)
y_predict # array([1])
y_predict[0] # 1
0xFF 总结
KNN算法是最简单有效的分类算法,简单且容易实现。当训练数据集很大时,需要大量的存储空间,而且需要计算待测样本和训练数据集中所有样本的距离,所以非常耗时
KNN对于随机分布的数据集分类效果较差,对于类内间距小,类间间距大的数据集分类效果好,而且对于边界不规则的数据效果好于线性分类器。
KNN对于样本不均衡的数据效果不好,需要进行改进。改进的方法时对k个近邻数据赋予权重,比如距离测试样本越近,权重越大。
KNN很耗时,时间复杂度为O(n),一般适用于样本数较少的数据集,当数据量大时,可以将数据以树的形式呈现,能提高速度,常用的有kd-tree和ball-tree。

