插入排序（重点）

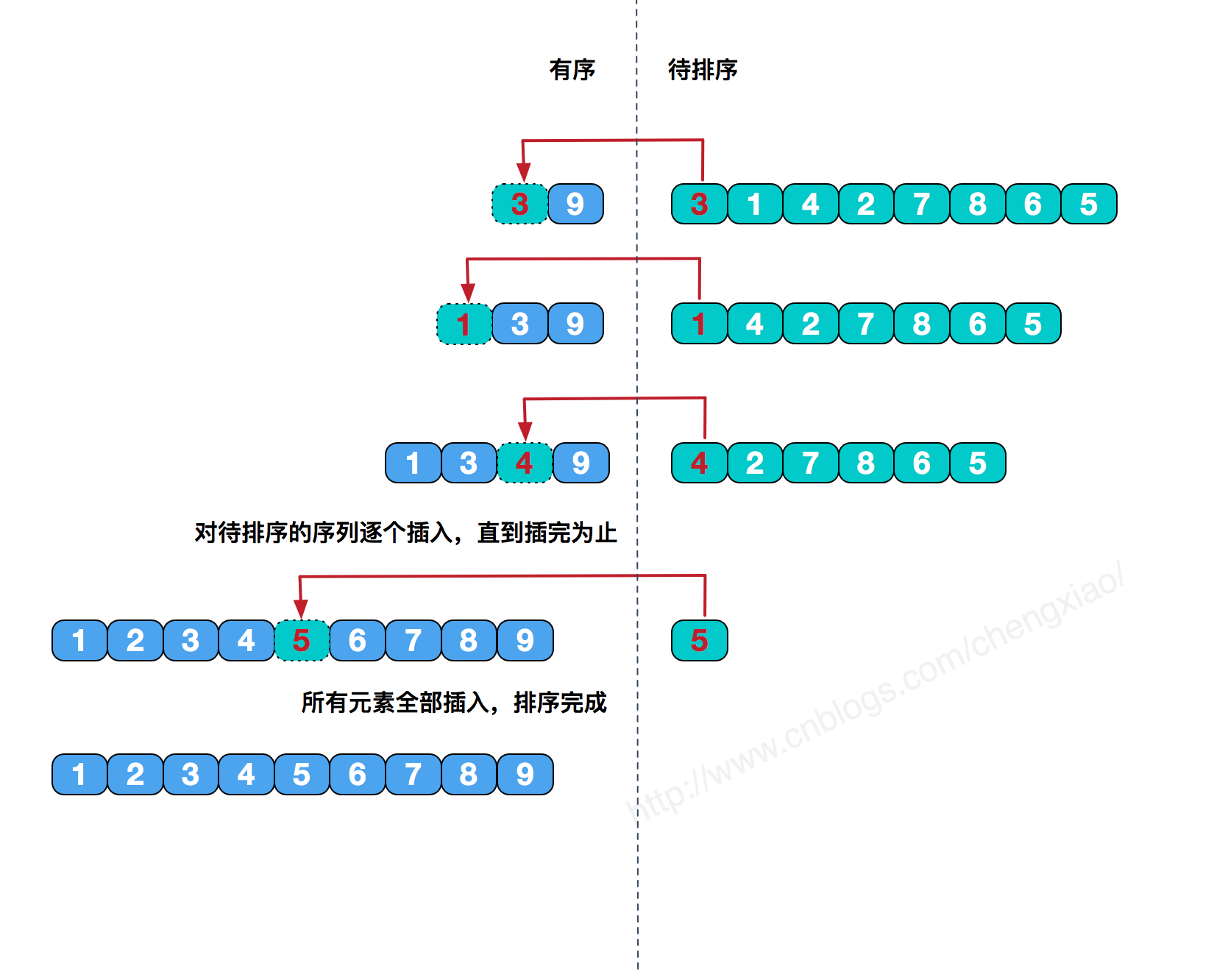
直接插入排序

每一步将一个待排序的记录，插入到前面已经排好序的有序序列中去，直到插完所有元素为止。

数据结构（十七）排序 - 图1

  1. /*
  2.  * 直接插入排序
  3.  * a -- 待排序的数组
  4.  * n -- 数组的长度
  5.  */
  6. void insert_sort(int a[], int n)
  7. {
  8.     int i, j, k;
  10.     for (i = 1; i < n; i++)
  11.     {
  12.         //为a[i]在前面的a[0...i-1]有序区间中找一个合适的位置
  13.         for (j = i - 1; j >= 0; j--)
  14.             if (a[j] < a[i])
  15.                 break;
  17.         //如找到了一个合适的位置
  18.         if (j != i - 1)
  19.         {
  20.             //将比a[i]大的数据向后移
  21.             int temp = a[i];
  22.             for (k = i - 1; k > j; k--)
  23.                 a[k + 1] = a[k];
  24.             //将a[i]放到正确位置上
  25.             a[k + 1] = temp;
  26.         }
  27.     }
  28. }

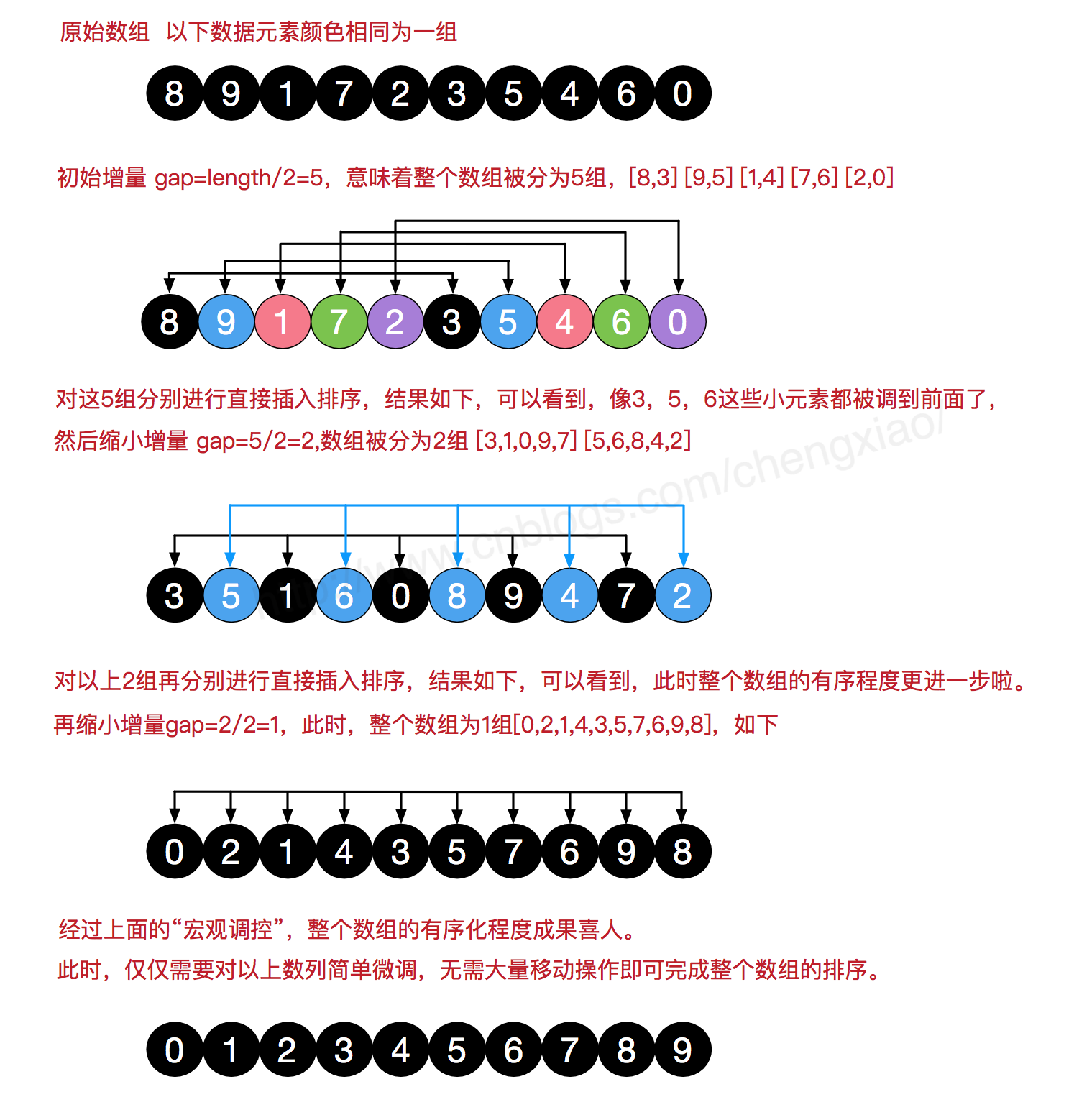
希尔排序

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

数据结构（十七）排序 - 图2

交换思想的排序（重点）

冒泡排序

对相邻的元素进行两两比较，顺序相反则进行交换，这样，每一趟会将最小或最大的元素“浮”到顶端，最终达到完全有序。

数据结构（十七）排序 - 图3

  1. #include <stdio.h>
  2. #include <stdlib.h>
  4. void main()
  5. {
  6.     int a[10] = {5,1,6,9,8,3,4,6,10,7};; //待排序整型数组
  8.     int temp= 0; //中间变量
  10.     //冒泡法排序实现从小到大排序
  11.     for(int i=0;i<10;i++) //进行10次循环
  12.     {
  13.         for(int j=i+1;j<10;j++) //循环比较剩余的变量
  14.         {
  15.             if(a[i] > a[j]) //如果前面一个数比后面数大，交换两个数的值
  16.             {
  17.                 temp = a[i];
  18.                 a[i] = a[j];
  19.                 a[j] = temp;
  20.             }
  21.         }
  22.     }
  24.     for(int i=0;i<10;i++) //循环输出排序以后的结果
  25.     {
  26.         printf("%d  ",a[i]);
  27.     }
  29.     system("pause");
  30. }

快速排序

  1. 在数据集之中，选择一个元素作为”基准”（pivot）。
  2. 所有小于”基准”的元素，都移到”基准”的左边；所有大于”基准”的元素，都移到”基准”的右边。
  3. 对”基准”左边和右边的两个子集，不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

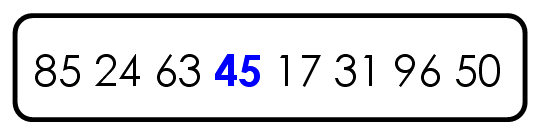
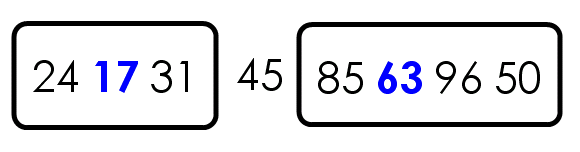
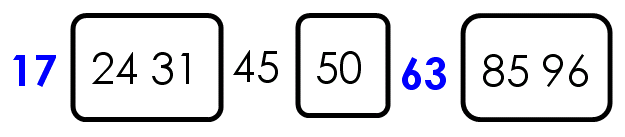
举例来说，现在有一个数据集{85, 24, 63, 45, 17, 31, 96, 50}，怎么对其排序呢？
第一步，选择中间的元素45作为”基准”。（基准值可以任意选择，但是选择中间的值比较容易理解。）

数据结构（十七）排序 - 图4

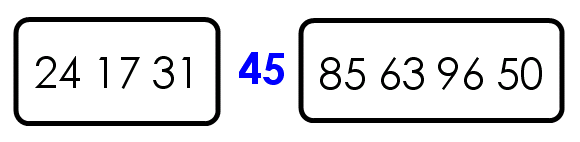
第二步，按照顺序，将每个元素与”基准”进行比较，形成两个子集，一个”小于45”，另一个”大于等于45”。（先从右边往左找）

数据结构（十七）排序 - 图5

第三步，对两个子集不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

数据结构（十七）排序 - 图6

数据结构（十七）排序 - 图7

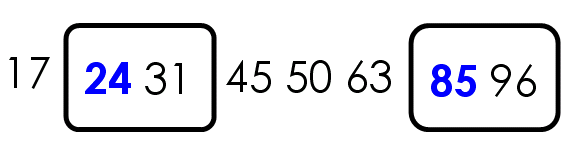
数据结构（十七）排序 - 图8

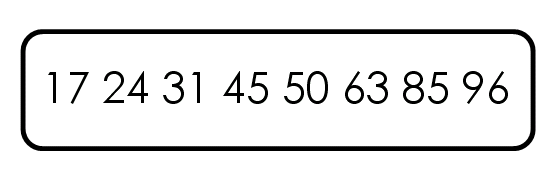
数据结构（十七）排序 - 图9

选择排序（重点）

简单选择排序

每一趟从待排序的数据元素中选择最小（或最大）的一个元素作为首元素，直到所有元素排完为止，简单选择排序是不稳定排序。在所有排序方法中，关键字比较的次数与记录的初始排列次序无关的是选择排序。

示例


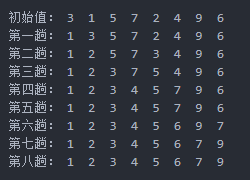
image.png

  1. // 输出数组内容
  2. void print(int array[], int length, int i) {
  3.     printf("i=%d:",i);
  4.     for (int j = 0; j < length; j++) {
  5.         printf(" %d ", array[j]);
  6.     }
  7.     printf("\n");
  8. }
  10. // 获取数组最小值下标
  11. int SelectMinKey(int array[], int length, int i) {
  12.     int k = i;
  13.     for (int j = i + 1; j < length; j ++) {
  14.         if (array[k] > array[j]) {
  15.             k = j;
  16.         }
  17.     }
  18.     return k;
  19. }
  21. // 简单选择排序（Simple Selection Sort）
  22. void SelectSort(int array[], int length) {
  23.     int key, temp;
  24.     for (int i = 0; i < length; i ++) {
  25.         key = SelectMinKey(array, length, i); // 获取最小元素的下标
  26.         if (key != i) { // 最小元素与第i位置元素交换
  27.             temp = array[i];
  28.             array[i] = array[key];
  29.             array[key] = temp;
  30.         }
  31.         print(array, length, i);
  32.     }
  33. }
  35. int main(int argc, const char * argv[]) {
  36.     int arraySelectSort[8] = { 3, 1, 5, 7, 2, 4, 9, 6 };
  37.     SelectSort(arraySelectSort, 8);
  38.     printf("\n");
  40.     return 0;
  41. }

堆排序

堆

具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

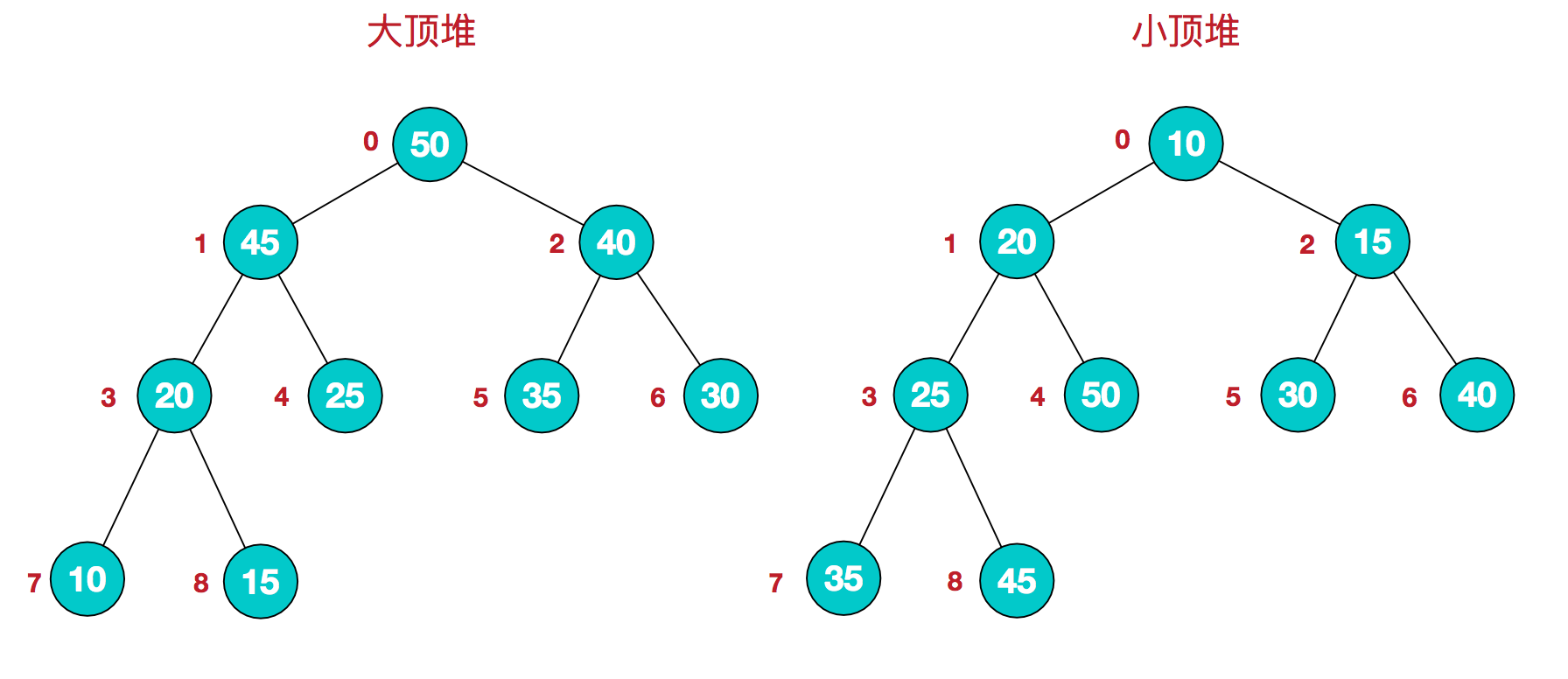
数据结构（十七）排序 - 图11

同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子

数据结构（十七）排序 - 图12

实现思路

  1. 将无序列表序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
  2. 将堆顶元素与末尾元素交换，将最大元素”沉”到数组末端;
  3. 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

时间复杂度

对任意分支节点进行筛选运算的时间复杂度为 O(logn)，整个堆排序过程的时间复杂度为 O(n*logn)。

其他排序（重点）

归并排序

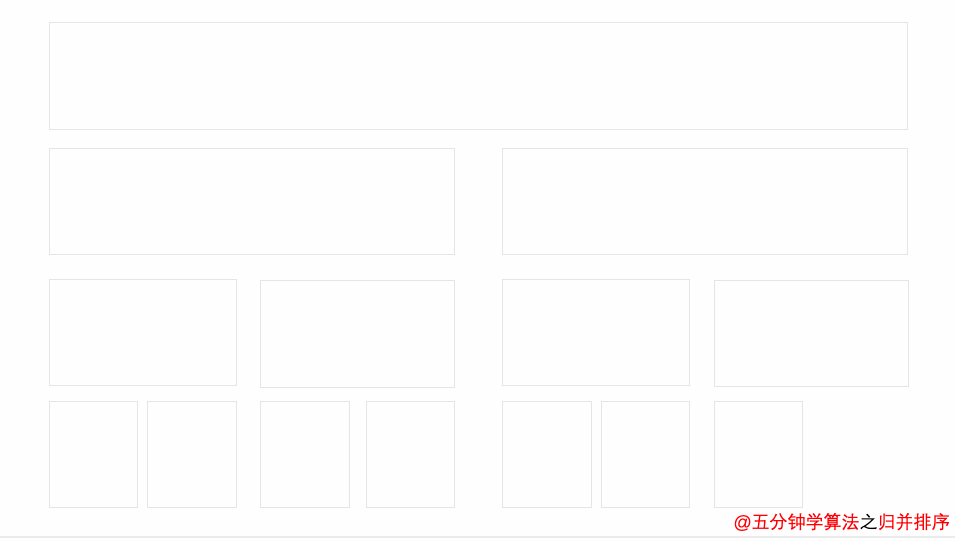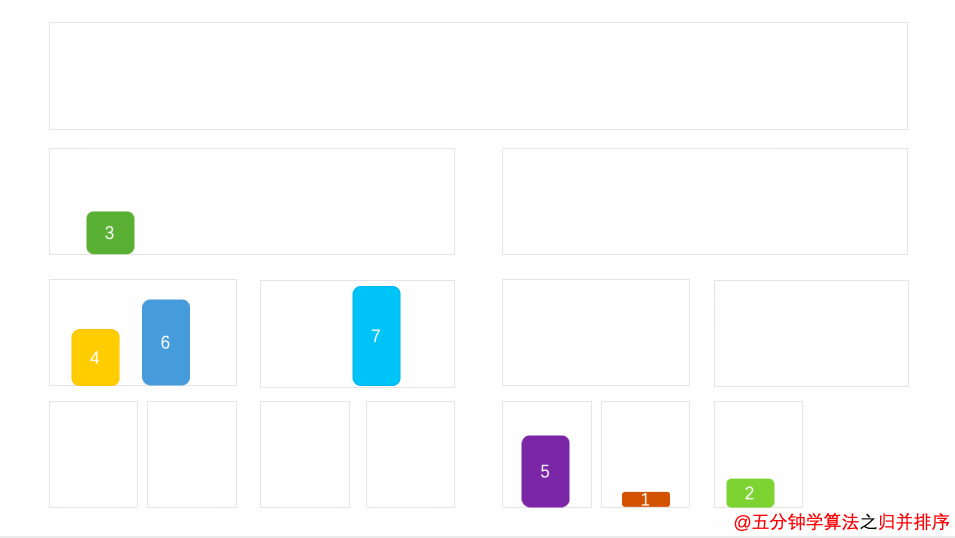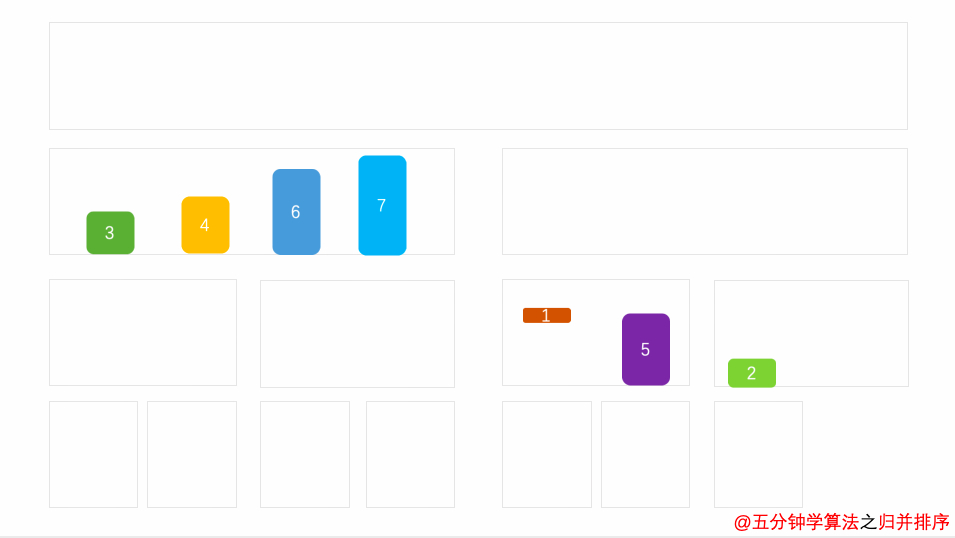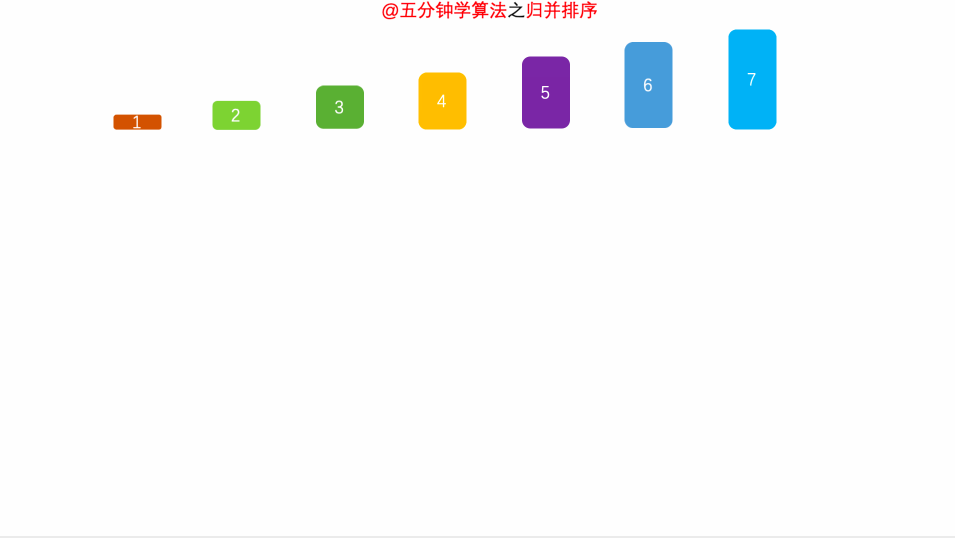
数据结构（十七）排序 - 图13

  • 首先，将数字分割成两片区域
  • 直到每片区域只有一个元素
  • 分割完成
  • 接下来，将分割的每片区域进行合并组合
  • 合并时，按照数字的升序移动，使得合并后的数字在组内按升序排列
  • 当合并包含多个数字的组时，比较开头的数字，移动其中较小的数字
  • 比如在动画中，比较开头的 4 和 3
  • 其中 4 大于 3， 因此移动 3
  • 按照同样的逻辑去比较该列剩余的头数
  • 4 小于 7 ，所以移动 4
  • 递归的重复组的合并操作，直到所有数字都在一个组中。
  1. #include<stdio.h>
  3. #define Max_ 10
  4. // 打印结果
  5. void Show(int  arr[], int n)
  6. {
  7.     int i;
  8.     for ( i=0; i<n; i++ )
  9.         printf("%d  ", arr[i]);
  10.     printf("\n");
  11. }
  13. // 归并排序中的合并算法
  14. void Merge(int array[], int left, int m, int right)
  15. {
  16.     int aux[Max_] = {0};  // 临时数组 （若不使用临时数组，将两个有序数组合并为一个有序数组比较麻烦）
  17.     int i; //第一个数组索引
  18.     int j; //第二个数组索引
  19.     int k; //临时数组索引
  21.     for (i = left, j = m+1, k = 0; k <= right-left; k++) // 分别将 i, j, k 指向各自数组的首部。
  22.     {
  23.         //若 i 到达第一个数组的尾部，将第二个数组余下元素复制到 临时数组中
  24.         if (i == m+1)
  25.         {
  26.             aux[k] = array[j++];
  27.             continue;
  28.         }
  29.         //若 j 到达第二个数组的尾部，将第一个数组余下元素复制到 临时数组中
  30.         if (j == right+1)
  31.         {
  32.             aux[k] = array[i++];
  33.             continue;
  34.         }
  35.         //如果第一个数组的当前元素 比 第二个数组的当前元素小，将 第一个数组的当前元素复制到 临时数组中
  36.         if (array[i] < array[j])
  37.         {
  38.             aux[k] = array[i++];
  39.         }
  40.         //如果第二个数组的当前元素 比 第一个数组的当前元素小，将 第二个数组的当前元素复制到 临时数组中
  41.         else
  42.         {
  43.             aux[k] = array[j++];
  44.         }
  45.     }
  47.     //将有序的临时数组 元素 刷回 被排序的数组 array 中，
  48.     //i = left , 被排序的数组array 的起始位置
  49.     //j = 0， 临时数组的起始位置
  50.     for (i = left, j = 0; i <= right; i++, j++)
  51.     {
  52.         array[i] = aux[j];
  53.     }
  54. }
  56. // 归并排序
  57. void MergeSort(int array[], int start, int end)
  58. {
  59.     if (start < end)
  60.     {
  61.         int i;
  62.         i = (end + start) / 2;
  63.         // 对前半部分进行排序
  64.         MergeSort(array, start, i);
  65.         // 对后半部分进行排序
  66.         MergeSort(array, i + 1, end);
  67.         // 合并前后两部分
  68.         Merge(array, start, i, end);
  69.     }
  70. }
  72. int main()
  73. {   //测试数据
  74.     int arr_test[Max_] = { 8, 4, 2, 3, 5, 1, 6, 9, 0, 7 };
  75.     //排序前数组序列
  76.     Show( arr_test, Max_ );
  77.     MergeSort( arr_test, 0, Max_-1 );
  78.     //排序后数组序列
  79.     Show( arr_test, Max_ );
  80.     return 0;
  81. }

基数排序

通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616}，它的示意图如下：

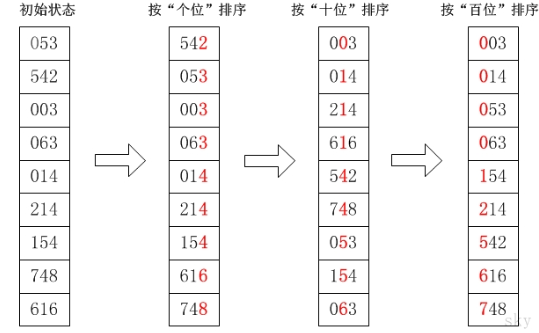
image.png

在上图中，首先将所有待比较数值变为统一位数长度，接着从最低位开始，依次进行排序：

  1. 按照个位数进行排序。
  2. 按照十位数进行排序。
  3. 按照百位数进行排序。

排序后，数列就变成了一个有序序列。

/**
 * 基数排序：C 语言
 */

#include <stdio.h>

// 数组长度
#define LENGTH(array) ( (sizeof(array)) / (sizeof(array[0])) )

/*
 * 获取数组a中最大值
 *
 * 参数说明：
 *     a -- 数组
 *     n -- 数组长度
 */
int get_max(int a[], int n)
{
    int i, max;

    max = a[0];
    for (i = 1; i < n; i++)
        if (a[i] > max)
            max = a[i];
    return max;
}

/*
 * 对数组按照"某个位数"进行排序(桶排序)
 *
 * 参数说明：
 *     a -- 数组
 *     n -- 数组长度
 *     exp -- 指数。对数组a按照该指数进行排序。
 *
 * 例如，对于数组a={50, 3, 542, 745, 2014, 154, 63, 616}；
 *    (01) 当exp=1表示按照"个位"对数组a进行排序
 *    (02) 当exp=10表示按照"十位"对数组a进行排序
 *    (03) 当exp=100表示按照"百位"对数组a进行排序
 *    ...
 */
void count_sort(int a[], int n, int exp)
{
    int output[n];             // 存储"被排序数据"的临时数组
    int i, buckets[10] = {0};

    // 将数据出现的次数存储在buckets[]中
    for (i = 0; i < n; i++)
        buckets[ (a[i]/exp)%10 ]++;

    // 更改buckets[i]。目的是让更改后的buckets[i]的值，是该数据在output[]中的位置。
    for (i = 1; i < 10; i++)
        buckets[i] += buckets[i - 1];

    // 将数据存储到临时数组output[]中
    for (i = n - 1; i >= 0; i--)
    {
        output[buckets[ (a[i]/exp)%10 ] - 1] = a[i];
        buckets[ (a[i]/exp)%10 ]--;
    }

    // 将排序好的数据赋值给a[]
    for (i = 0; i < n; i++)
        a[i] = output[i];
}

/*
 * 基数排序
 *
 * 参数说明：
 *     a -- 数组
 *     n -- 数组长度
 */
void radix_sort(int a[], int n)
{
    int exp;    // 指数。当对数组按各位进行排序时，exp=1；按十位进行排序时，exp=10；...
    int max = get_max(a, n);    // 数组a中的最大值

    // 从个位开始，对数组a按"指数"进行排序
    for (exp = 1; max/exp > 0; exp *= 10)
        count_sort(a, n, exp);
}

void main()
{
    int i;
    int a[] = {53, 3, 542, 748, 14, 214, 154, 63, 616};
    int ilen = LENGTH(a);

    printf("before sort:");
    for (i=0; i<ilen; i++)
        printf("%d ", a[i]);
    printf("\n");

    radix_sort(a, ilen);

    printf("after  sort:");
    for (i=0; i<ilen; i++)
        printf("%d ", a[i]);
    printf("\n");
}

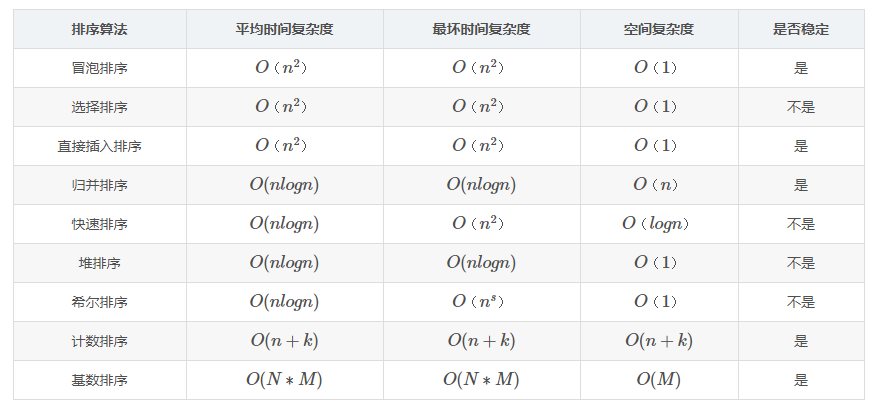
各种排序算法的比较

image.png

外部排序

外部排序方法

多路平衡归并

最佳归并树

参考

【1】图解排序算法(一)之3种简单排序(选择，冒泡，直接插入)
【2】图解排序算法(二)之希尔排序
【3】图解排序算法(三)之堆排序
【4】快速排序（Quicksort）的Javascript实现