搜索问题的定义

根据问题的时间情况，不断寻找可利用知识，从而构造一条代价最小的推理路线，使问题得以解决的过程称为搜索

适用情况

  • 难以获得所求解所需的全部信息
  • 没有现成的算法可供使用

图的遍历（重点）

定义

从已给的连通图的某个点出发，沿着一些边访遍所有的顶点，且使每个顶点紧被访问一次，就叫做图的遍历。

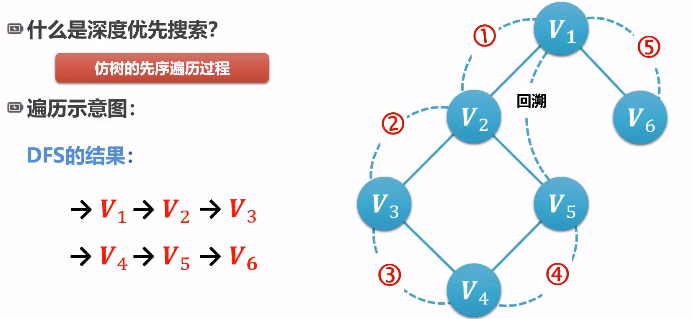
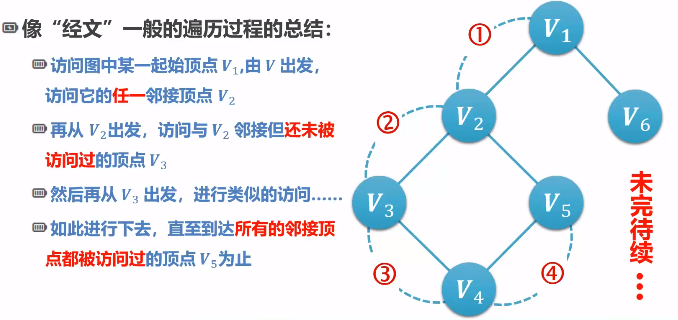
深度优先搜索 DFS

image.png
image.png
image.png

邻接表实现 DFS 算法

image.png

时间复杂度空间复杂度

DFS算法是一一个递归算法，需要借助一个递归工作栈，故它的空间复杂度为O ( N ) O(N)O(N)。
遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所采用结构。

邻接表表示时，查找所有顶点的邻接点所需时间为O ( E ) O(E)O(E)，访问顶点的邻接点所花时间为O ( N ) O(N)O(N),此时，总的时间复杂度为O ( N + E ) O(N+E)O(N+E)。

邻接矩阵表示时，查找每个顶点的邻接点所需时间为O ( N ) O(N)O(N)，要查找整个矩阵，故总的时间度为O ( N 2 ) O(N^2)O(N2)。

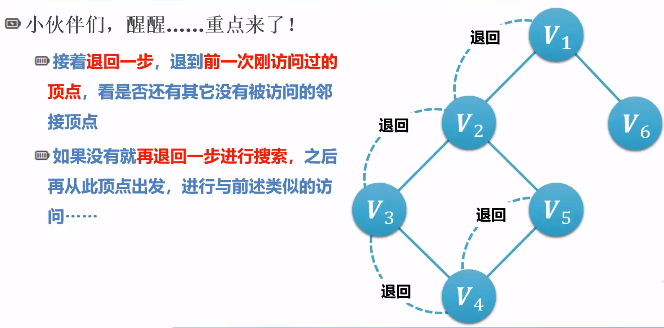
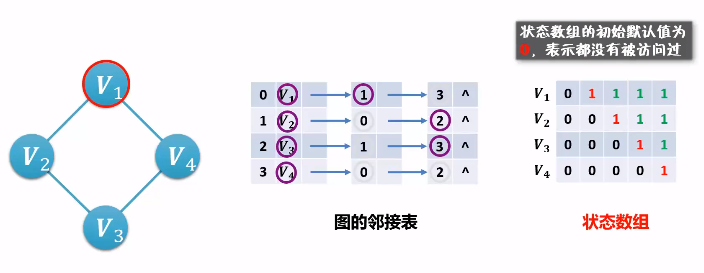
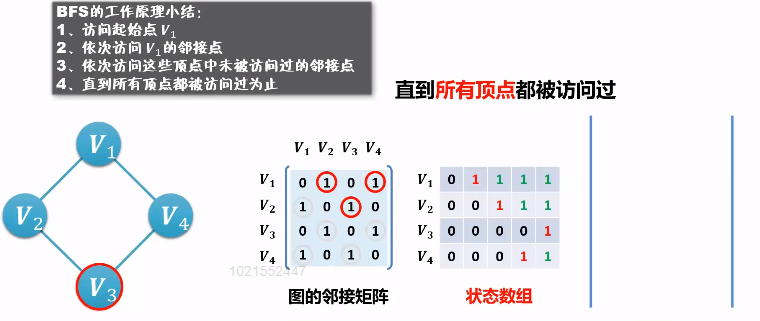
广度优先搜索 BFS

image.png

DFS 算法 VS BFS 算法

image.png

最小生成树（重点）

在连通网的所有生成树中，所有边的代价和最小的生成树

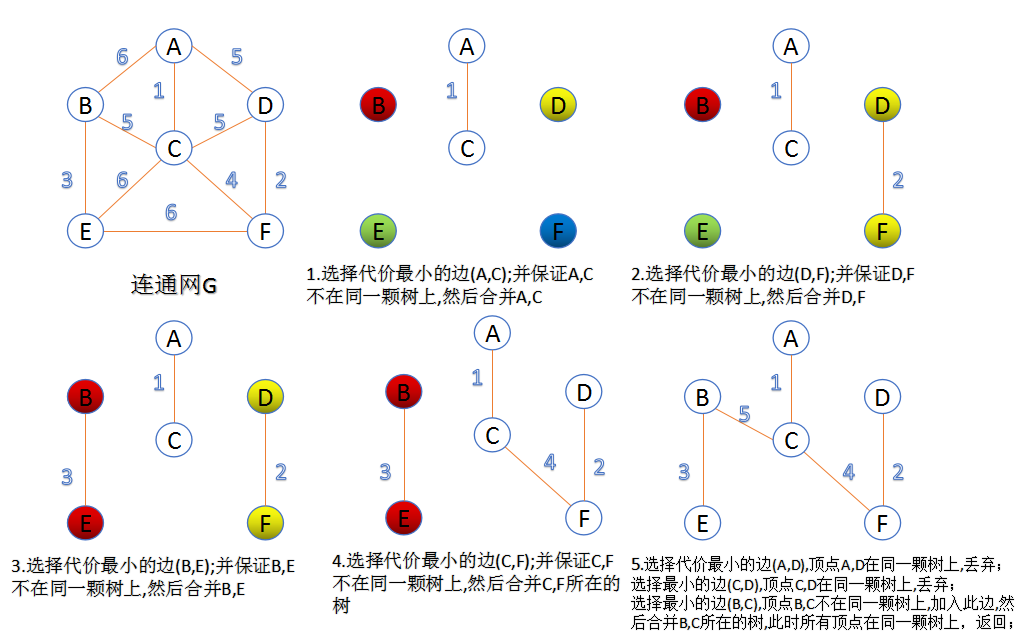
Kruskal 算法（克鲁斯卡尔算法）

此算法可以称为“加边法”，初始最小生成树边数为 0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

image.png
数据结构（十五）图的遍历、搜索 - 图8

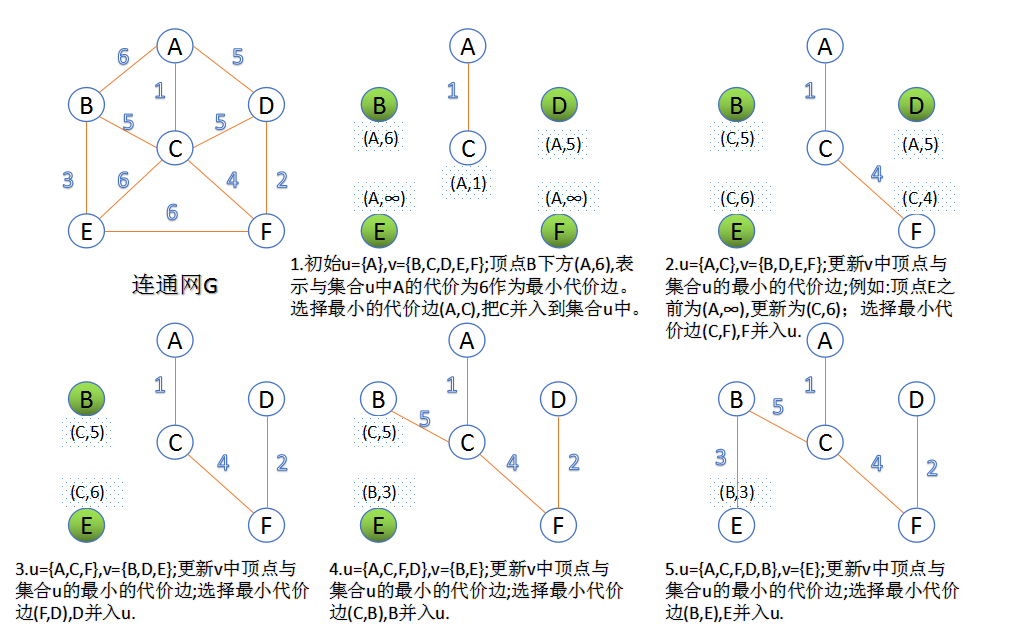
Prim 算法（普里姆算法）

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点 s 开始，逐渐长大覆盖整个连通网的所有顶点。

image.png
数据结构（十五）图的遍历、搜索 - 图10

拓扑排序

一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。

且该序列必须满足下面两个条件：

  1. 每个顶点出现且只出现一次。
  2. 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非 DAG 图没有拓扑排序一说。
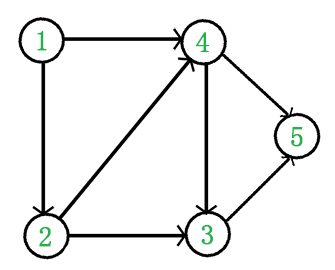
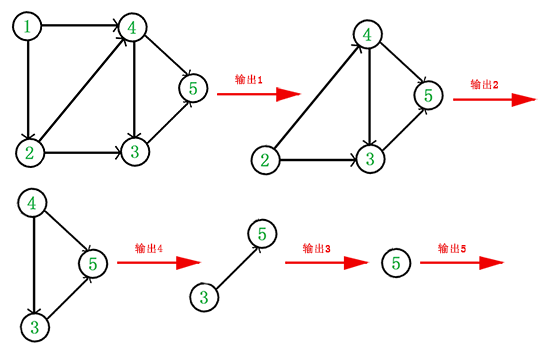
例如，下面这个图：

数据结构（十五）图的遍历、搜索 - 图11

它是一个 DAG 图，那么如何写出它的拓扑排序呢？

这里说一种比较常用的方法：

  1. 从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。
  2. 从图中删除该顶点和所有以它为起点的有向边。
  3. 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

数据结构（十五）图的遍历、搜索 - 图12

于是，得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。
通常，一个有向无环图可以有一个或多个拓扑排序序列。

最短路径（难点）

Floyd 算法（弗洛伊德算法）— 所有顶点间的最短路径

image.png

  1. #include <stdio.h>
  2.     int main()
  3.     {
  4.         int e[10][10],k,i,j,n,m,t1,t2,t3;
  5.         int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值
  6.         //读入n和m，n表示顶点个数，m表示边的条数
  7.         scanf("%d %d",&n,&m);
  8.         //初始化
  9.         for(i=1;i<=n;i++)
  10.             for(j=1;j<=n;j++)
  11.                 if(i==j) e[i][j]=0;
  12.                   else e[i][j]=inf;
  13.         //读入边
  14.         for(i=1;i<=m;i++)
  15.         {
  16.             scanf("%d %d %d",&t1,&t2,&t3);
  17.             e[t1][t2]=t3;
  18.         }
  19.         //Floyd-Warshall算法核心语句
  20.         for(k=1;k<=n;k++)
  21.             for(i=1;i<=n;i++)
  22.                 for(j=1;j<=n;j++)
  23.                     if(e[i][j]>e[i][k]+e[k][j] )
  24.                         e[i][j]=e[i][k]+e[k][j];
  25.         //输出最终的结果
  26.         for(i=1;i<=n;i++)
  27.         {
  28.          for(j=1;j<=n;j++)
  29.             {
  30.                 printf("%10d",e[i][j]);
  31.             }
  32.             printf("\n");
  33.         }
  34.         return 0;
  35.     }

Dijkstra 算法（迪杰斯特拉算法）— 单源最短路径

image.png

#include <stdio.h>
    int main()
    {
        int e[10][10],dis[10],book[10],i,j,n,m,t1,t2,t3,u,v,min;
        int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值
        //读入n和m，n表示顶点个数，m表示边的条数
        scanf("%d %d",&n,&m);
        //初始化
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
                if(i==j) e[i][j]=0;
                  else e[i][j]=inf;
        //读入边
        for(i=1;i<=m;i++)
        {
            scanf("%d %d %d",&t1,&t2,&t3);
            e[t1][t2]=t3;
        }
        //初始化dis数组，这里是1号顶点到其余各个顶点的初始路程
        for(i=1;i<=n;i++)
            dis[i]=e[1][i];
        //book数组初始化
        for(i=1;i<=n;i++)
            book[i]=0;
        book[1]=1;
        //Dijkstra算法核心语句
        for(i=1;i<=n-1;i++)
        {
            //找到离1号顶点最近的顶点
            min=inf;
            for(j=1;j<=n;j++)
            {
                if(book[j]==0 && dis[j]<min)
                {
                    min=dis[j];
                    u=j;
                }
            }
            book[u]=1;
            for(v=1;v<=n;v++)
            {
                if(e[u][v]<inf)
                {
                    if(dis[v]>dis[u]+e[u][v])
                        dis[v]=dis[u]+e[u][v];
                }
            }
        }
        //输出最终的结果
        for(i=1;i<=n;i++)
            printf("%d ",dis[i]);
        getchar();
        getchar();
        return 0;
    }

AOV 网

  1. 顶点表示活动，弧表示活动间的优先关系的有向图。
  2. AOV 网是有向无环图，即不应该带有回路，因为若带有回路，则会陷入死循环。
  3. 所有活动可排列成一个线性序列，使得每个活动的所有前驱都排在该活动的前面，我们把此序列叫做拓扑序列。
  4. AOV 网的拓扑序列不是唯一的。
  5. 只有完成了所有前驱事件后才可以进行后续事件。

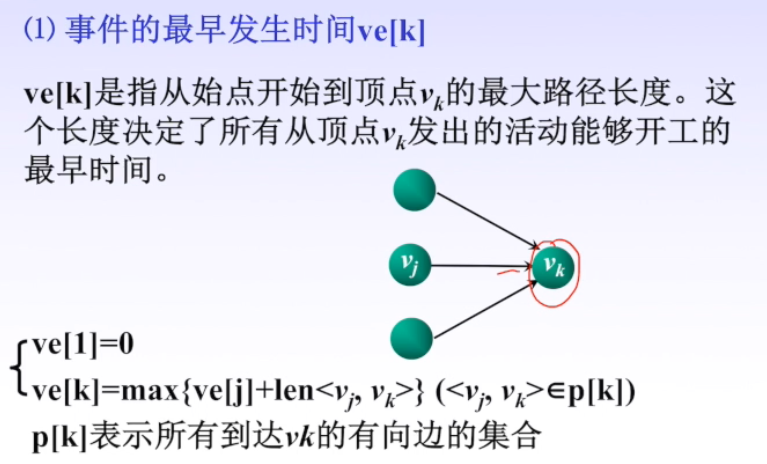
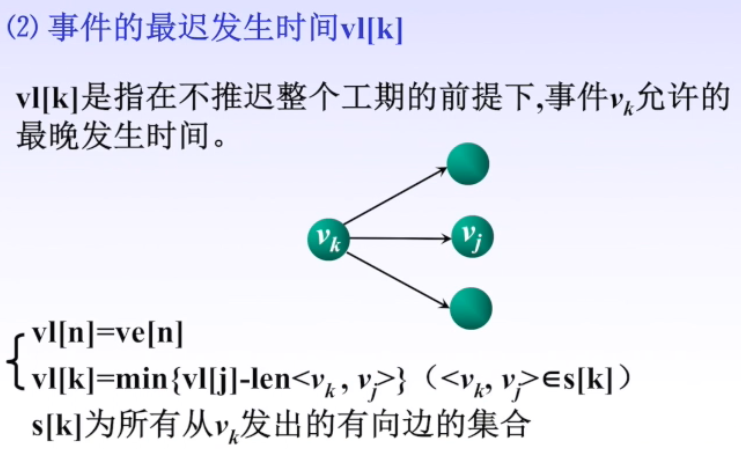
AOE 网

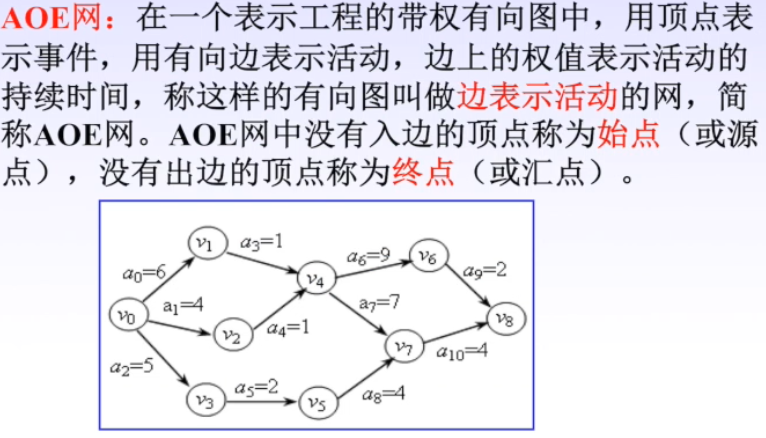
image.png

image.png

关键路径、关键活动

image.png

image.png
image.png
image.png
image.png