算法简介
算法定义
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
算法特征
- 输入输出:算法具有零个或者多个输入,最少有一个或者多个输出。
- 有穷性:指算法的每一个步骤都有确定的含义,不会出现二义性。
- 可行性:算法的每一步都必须是可行的,也就是说,每一步都能够通过执行有限次数完成。
算法设计的要求
- 正确性:算法的正确性是指算法至少具有输入、输出和加工处理无歧义性、能正确反应问题的需求、能够得到问题的正确答案。
- 易读性:算法设计的另一目的是为了方便阅读、理解和交流。
- 强壮性:当输入数据不合法时,算法也能做出相关的处理,而不是产生异常或者莫名其妙的结果。
- 高效率
二分查找法
二分查找法输入必须是一个有序序列,如果要查找的位置在列表中,返回位置,否则返回 null。每次取中间的数字作为基准值,如果比基准值大,新的基准值为右面的“中间值”,否则为左边的“中间值”。
运行时间
选择运行效率最高的算法,以最大地减少运行时间或占用空间。二分查找法的时间复杂度为 log(时间)。
大 O 表示法
仅知道算法需要多少时间才能执行完毕还不够,还需要知道运行时间如何随列表增长而增加。这才是大 O 表示法的真正用武之地。大 O 表示法让你能比较操作数,它指出了运行时间的递增。大 0 表示法指出了最坏情况下的运行时间。
推导方式
- 用常数 1 代替运行时间中的所有加法常量。
- 在修改后的运行次数函数中,只保留最高阶乘。
- 如果最高阶存在且不是 1,则去除与这个项目相乘的常数。
得到的就是大 O 阶。
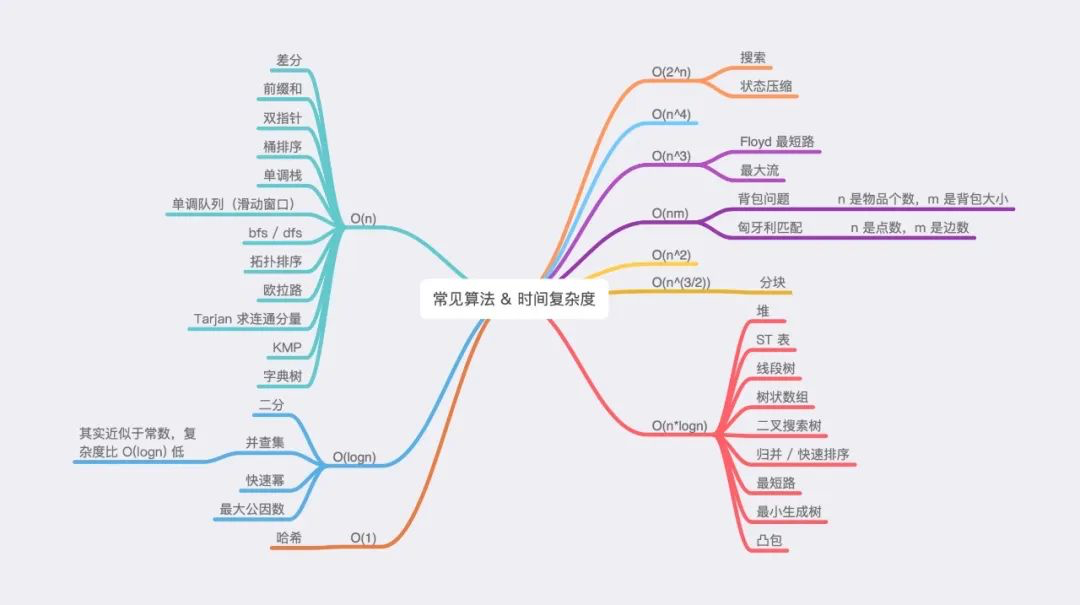
算法时间复杂度总结
选择排序
内存的工作原理
需要储存数据时,请求计算机提供存储空间,计算机给你一个地址。
数组和链表
额外请求的位置可能用不上,这将浪费内存。
数组和链表的运行时间
| 数组 | 链表 | |
|---|---|---|
| 读取 | O(1) | O(n) |
| 插入 | O(n) | O(1) |
使用链表插入元素更简单,如果没有足够的空间需要将数组复制到其他地方。删除元素,链表也是也是更好的选择,只需要更改前一个元素的指向的指针,把删除元素释放即可。而数值在删除元素后,必须将后面的元素都向前移动。使用数组访问元素更方便,因为它支持随机访问,而链表只能顺序访问。
选择排序
每一次找出最大值放到新的序列中,直到所有的值都添加到新的序列。因为大 O表示法会忽略诸如 1/2 这样的常数,所以这个算法的时间复杂度为 O(n)。
递归
如果使用循环,程序的性能可能更高;如果使用递归,程序可能更容易理解。如何选择看什么对你更重要。
基线条件和递归条件
每一个递归函数都有两个部分:基线条件和递归条件。递归条件就是自己调用自己,而基线条件是指函数不再调用自己,从而避免形成无限循环。
栈
调用另一个函数时,当前函数暂停并处于未完成状态。
虽然栈很方便,但是要付出代价:储存详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存,如果栈很高,就意味着存储了大量函数调用的信息。在这种情况下,你有两种选择:
- 重新编写代码,转而使用循环。
- 使用尾递归。
快速排序
D&C 算法解决问题的过程:
- 找出基线条件,这种条件必须尽可能简单。
- 不断将问题分解(或者说缩小规模),直到找到符合基线条件。
快速排序算法
首先,从数组中选择一个元素,这个元素作为基准值。接下来,找出比基准值小的元素以及比基准值大的元素。这个过程被称为分区。对这些分区递归进行快速排序。
该算法的时间复杂度为O(n logn)。
散列表
散列函数必须满足一下要求:
- 它必须是一致的。
- 将不同的输入映射到不同的数字。
应用
- 模拟映射关系
- 防止重复
- 缓存、记住数据,以免服务器再通过处理来生成它们。
冲突
一个简单的解决冲突的方法就是在相同的位置创建链表,如果链表很长散列表的速度将急速下降。
性能
在使用散列表时,避开最糟糕的情况很重要。避免冲突有以下需求:
- 较低的填充因子。
- 良好的散列函数。
填充因子
填充因子 = 散列表包含的元素数 / 位置总数
散列因子越低,发生冲突的可能性就越小。一旦填装因子大于 0.7,就调整散列表的长度。
良好的散列函数
SHA 函数
参考
【1】算法图解
【2】大话数据结构
【3】2021 春招冲刺攻略