广度优先搜索

解决最短路径问题的算法被称作广度优先搜索算法。

问题描述

查找你的朋友是否为芒果经销商，如果都不是，查找你的朋友的朋友是否是芒果经销商。

实现算法

  1. 创建一个队列，用于存储要检查的人。
  2. 从队列中弹出一个人。
  3. 检查这个人是否芒果经销商。
    1. 是，大功告成。
    2. 否，将这个人加入队列。
  4. 回到第 2 步。
  5. 如果队列为空，说明你的人际关系网中没有芒果经销商。

检查完一个人你需要标记他（她），如果他（她）是其他人的朋友不再检查他（她）。需要用一个列表来记录检查过的人。

运行时间

广度优先搜索的时间为 O(V+E)，V 为顶点数，E 为边数。

狄克斯拉特算法

  1. 找到最便宜的节点，即可在最短时间前往的节点。
  2. 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。
  3. 重复这个过程，直到对图中的每个节点都这么做了。
  4. 计算最终路线。

狄克斯拉特算法用于每条边都有关联数字的图，这些数字称为权重。
带权重的图称为加权图，不带权重的图称为非加权图。
狄克斯拉特算法只适应于正有权路径，而非有权路径和有负权边的图都不能使用狄克斯拉特算法。

贪婪算法

教室调度问题

问题描述

将以下课程尽可能安排在一个教室中。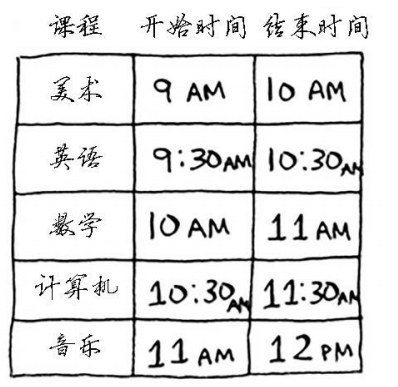
image.png

实现算法

  1. 选择结束最早的课，它就是在这间教室上的第一堂课。
  2. 选择第一堂课结束后才开始的课。同样，你选择结束最早的课，这将是在这间教室上的第二堂课。
  3. 重复，得到最后结果。

背包问题

问题描述

假设你是个小偷，背着可装 35 磅（1 磅 ≈ 0.45 千克）重的背包，在商场偷窃各种可装入背包的商品。你力图装入价值最高的商品。

实现算法

  1. 盗窃可装入背包的最贵商品。
  2. 再盗窃可装入背包的最贵商品，以此类推。

贪婪算法未必每次都会得到最优解，它会得到一个最优解相接近的方案。

如何区分 NP 完全问题

  • 元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
  • 涉及“所有组合”的问题通常是 NP 完全问题。
  • 不能将问题分为小问题，必须考虑各种可能的情况。这可能是 NP 完全问题。
  • 如果问题涉及序列难以解决，它可能是 NP 完全问题。
  • 如果问题涉及集合难以解决，它可能就是 NP 完全问题。
  • 如果问题可以转换为集合覆盖问题或者旅行商的问题，那它肯定是 NP 完全问题。

动态规划

背包问题

问题描述

假设你是个小偷，背着可装 4 磅（1 磅 ≈ 0.45 千克）重的背包，在商场偷窃各种可装入背包的商品。你可以装入背包1的物品有以下三件，你应该如何选择?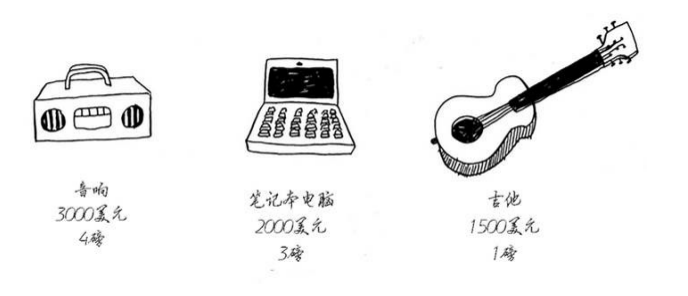
image.png

简单算法

尝试各种可能性的组合，并找出价值最高的组合。这种算法时间复杂度为 O（2）。

动态规划

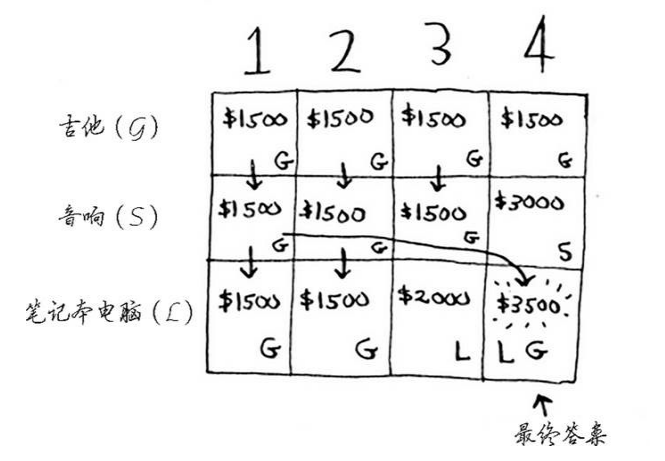
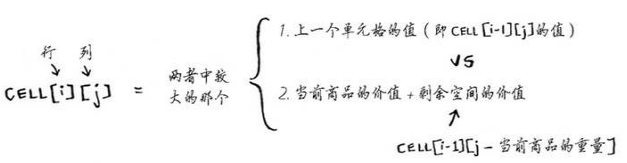
image.png
image.png

  • 动态规划可帮助你在给定约束条件下找到最优解。
  • 在问题可被分解为彼此独立且分散的子问题时，就可以使用动态规划来解决。
  • 每种动态规划解决方案都涉及网格。
  • 单元格中的值就是你要的最优值。
  • 每个单元格就是一个子问题，因此你应该考虑如何将问题分成若干个子问题，这有助于你找出网格的坐标轴。

K 最近邻算法

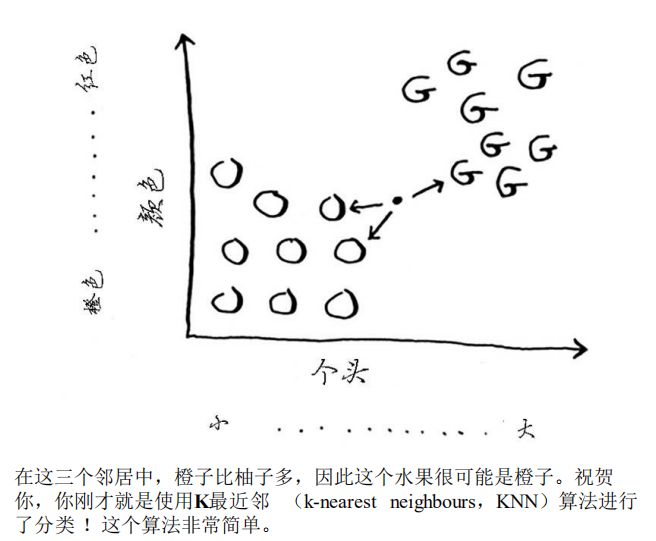
image.png

回归

  • 分类就是编组
  • 回归就是预测结果

选择合适的特征

  • 与要推荐的电影紧密相关的特征。
  • 不偏不倚的特征

参考

【1】算法图解