数组存储地址的运算（次重点）
稀疏矩阵的三元组表示法（次重点）
目的
对于在实际问题中出现的大型的稀疏矩阵，若用常规分配方法在计算机中储存，将会产生大量的内存浪费，而且在访问和操作的时候也会造成大量时间上的浪费，为了解决这一问题，从而善生了多种解决方案。
具体做法
由于其自身的稀疏特性，通过压缩可以大大节省稀疏矩阵的内存代价。
具体操作是：将非零元素所在的行、列以及它的值构成一个三元组（i,j,v），然后再按某种规律存储这些三元组，这种方法可以节约存储空间。具体如下图：
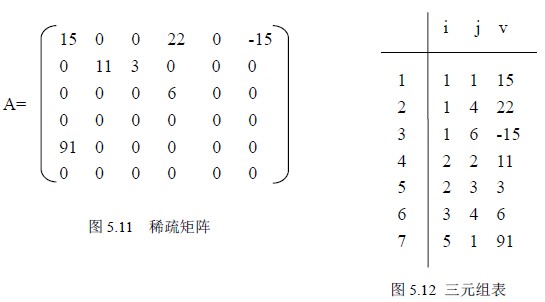
在用三元组表示稀疏矩阵，每个元素要用行号,列号,元素值来表示，还要三个成员来记住,矩阵的行数列数，总的元素数。
三对角矩阵
三对角矩阵ai,j在一维数组B存放的下标K=2i+j-3
若有收获，就点个赞吧
0 人点赞
