树的定义

n 个结点的有限集

image.png

结点个数为零的书为空树（n = 0）；任意一个非空树中有且只有一个特定的称为根的结点。非根的结点可以分为互不相交的有限集，每个集合本身又是一棵树，这些树称为根的子树。

一些基本概念

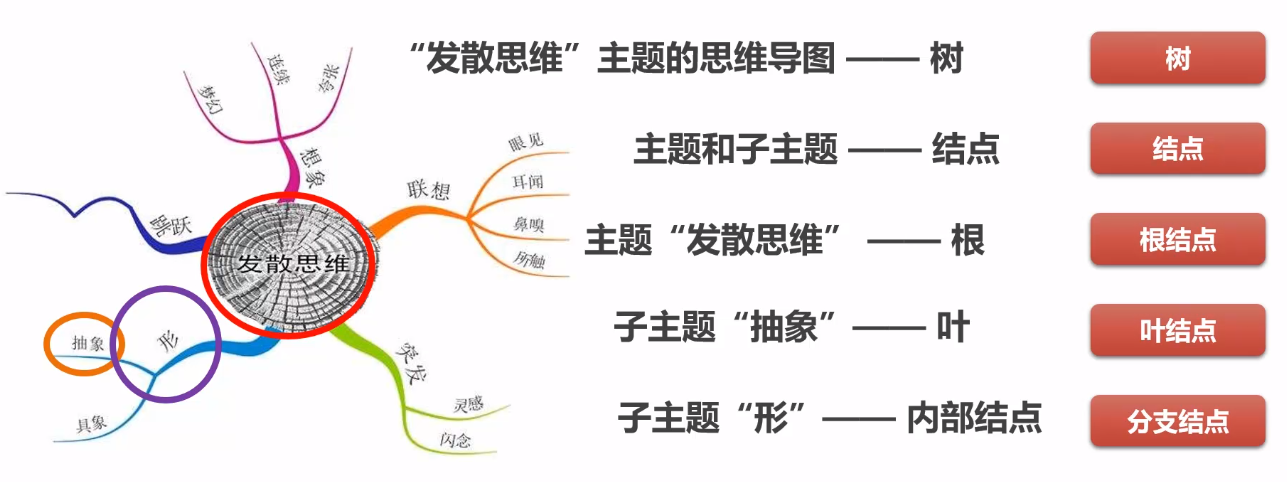
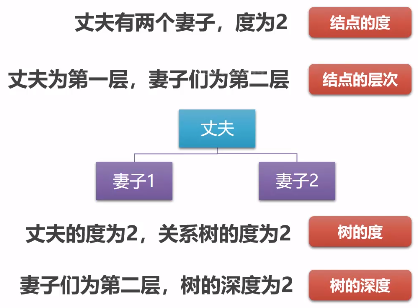
image.png

image.png

在树中，结点的度是指节点孩子的个数，树中结点最大的度称为树的度。树的深度是指树有几层。

image.png

森林：删除根结点后不相交的树的集合。
树的分类

  • 有序树：结点各子树从左至右有序，不能互换（左为第一）
  • 无序树：结点各子树可以互换位置。

树中结点总数为n=分支数+1，分支数等于树中各结点的度之和。

树的几种表示方法

孩子表示法

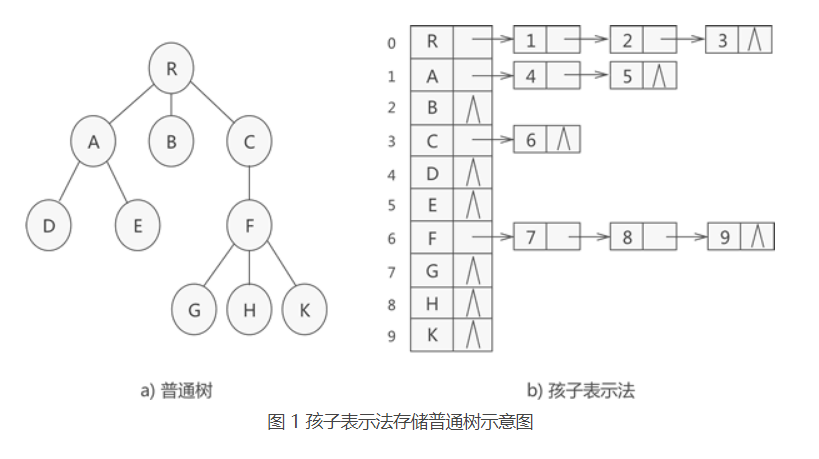
image.png

  1. //孩子表示法
  2. typedef struct CTNode{
  3.     int child;//链表中每个结点存储的不是数据本身，而是数据在数组中存储的位置下标
  4.     struct CTNode * next;
  5. }ChildPtr;
  6. typedef struct {
  7.     TElemType data;//结点的数据类型
  8.     ChildPtr* firstchild;//孩子链表的头指针
  9. }CTBox;
  10. typedef struct{
  11.     CTBox nodes[MAX_SIZE];//存储结点的数组
  12.     int n,r;//结点数量和树根的位置
  13. }CTree;

孩子兄弟表示法

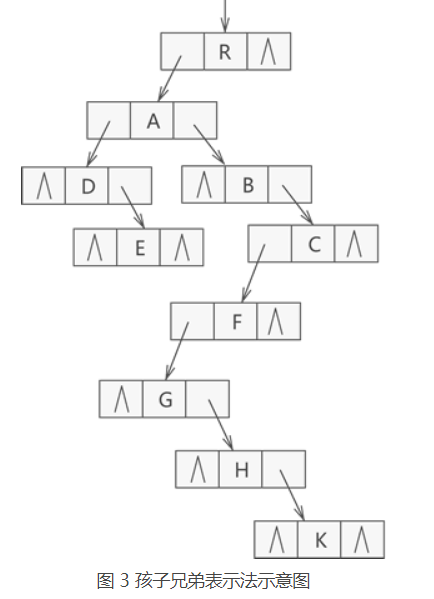
image.png
image.png

#define ElemType char
typedef struct CSNode{
    ElemType data;
    struct CSNode * firstchild,*nextsibling;
}CSNode,*CSTree;

双亲表示法

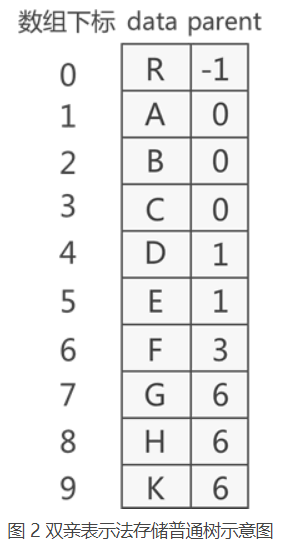
image.png

#define MAX_SIZE 100//宏定义树中结点的最大数量
typedef char ElemType;//宏定义树结构中数据类型
typedef struct Snode{
    TElemType data;//树中结点的数据类型
    int parent;//结点的父结点在数组中的位置下标
}PTNode;
typedef struct {
    PTNode tnode[MAX_SIZE];//存放树中所有结点
    int n;//根的位置下标和结点数
}PTree;

二叉树定义

二叉树是 n （n>=0）个结点所构成的集合。它或为空树（n=0）；或为非空树，对于非空树T：有且只有一个结点，除根以外的其余结点分为两个互不相交的子集 T1 和 T2，分别称为 T 的左子树和右子树，且 T1 和 T2 本身又都是二叉树。

二叉树与普通树的异同

image.png

二叉树的几种形态

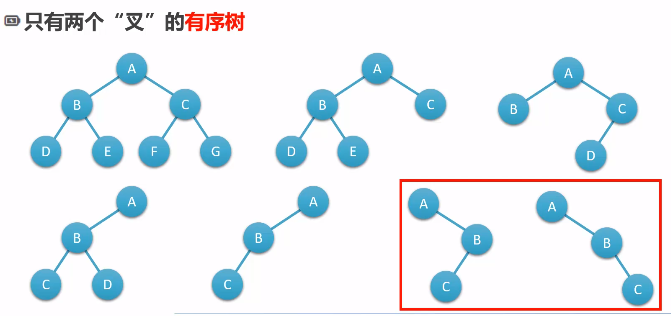
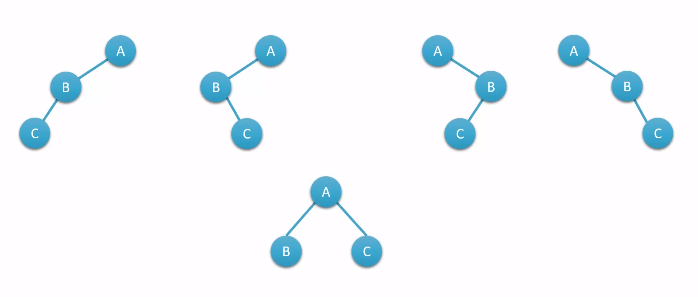
image.png

image.png

为什么研究二叉树

普通（多叉树）不转换为二叉树，运算很难实现。

为什么重点研究每个结点最多只有两个“叉”的树

  • 二叉树的结构最简单，规律最强。
  • 可以证明，所有树都能转化为唯一对应的二叉树，不失一般性。

二叉树的性质（重难点）

  • 在二叉树的第 i 层上最多有 2i-1 个结点。
  • 深度为 k 的二叉树最多有 2k-1 个结点。
  • 对于任何一颗二叉树，若 2 度的结点有 n2 个，则叶子树 n0 必定为 n2+1（即 n0 = n2 + 1）。
  • 节点数=分支数+1

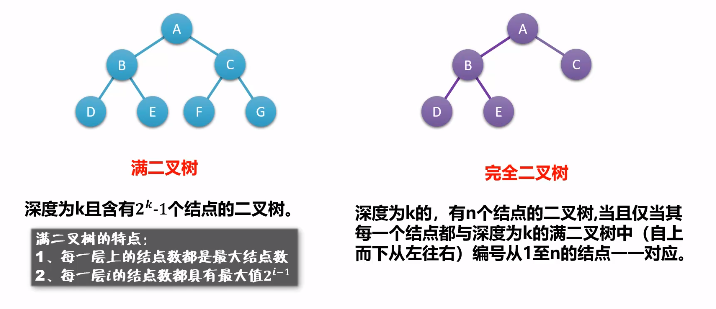
满二叉树和完全二叉树

image.png
image.png

完全二叉树的特点

  • 叶结点只能出现在最下两层
  • 最下层的叶结点一点集中在左部连续位置
  • 倒数第二层若有叶结点，一定都在右部连续位置
  • 如果结点度为 1，则结点只有右孩子
    • 即不存在右子树的情况
  • 同样结点树的二叉树，完全二叉树的深度是最小的。
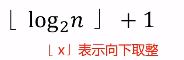
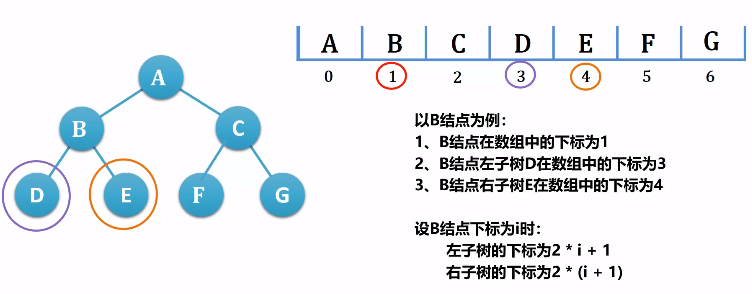
  • 具有 n 个结点的完全二叉树的深度为image.png
  • 若从上至下、从左到右编号，则编号为 i 的结点，其左孩子编号为 2i ，其右孩子编号必为 2i+1；其双亲编号必为 [i/2]。

二叉树的顺序存储结构

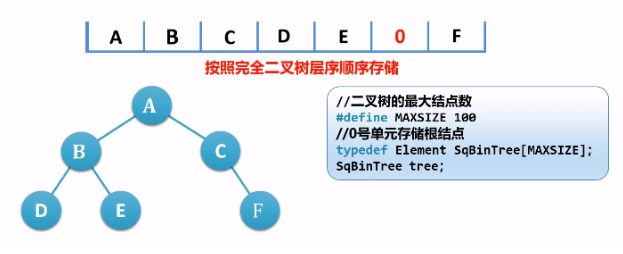
image.png
这种顺序存储结构会造成存储空间的浪费。

创建二叉树


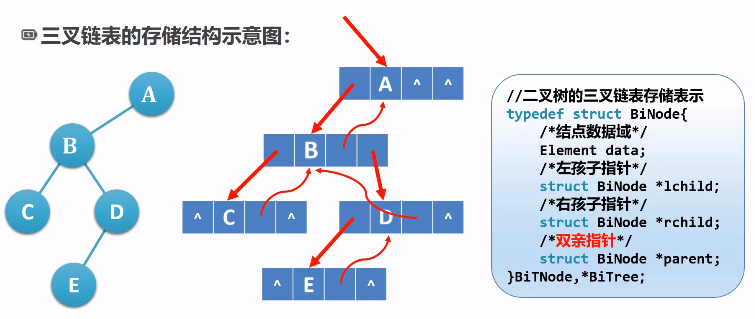
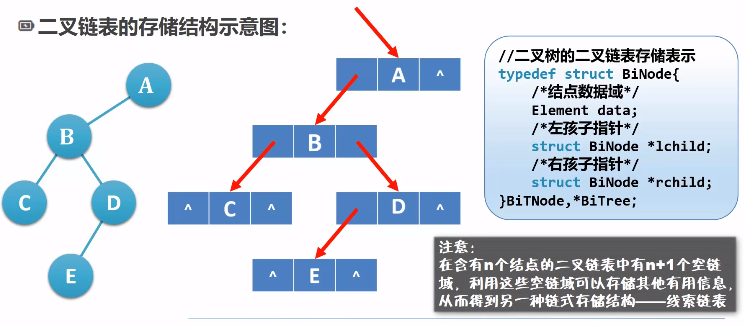
image.png

二叉树的链式存储结构

image.png

三叉树的链式存储结构


image.png

二叉排序树（BST）

  • 若左子树非空，则左子树上所有值均小于根结点
  • 若右子树非空，则右子树上所有值均大于根结点
  • 左、右子树也分别是一颗二叉排序树

平衡二叉树（AVL）

定义：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

高度为N的结点推导公式：Cn=Cn-1+Cn-2+1,C1=1,C2=2

平衡因子：左右子树的高度差