数据结构（十二）树的遍历和表示法

遍历定义

遍历是树形结构插入、删除、修改、查找和排序的前提，是二叉树一切运算的基础和核心。
按照某条路线遍访每一个结点且不重复（又称周游）。
遍历二叉树——从根结点触发，按照某种次序依次访问二叉树中所有的结点，使得每个结点只被依次访问一次。

遍历方法（重点）

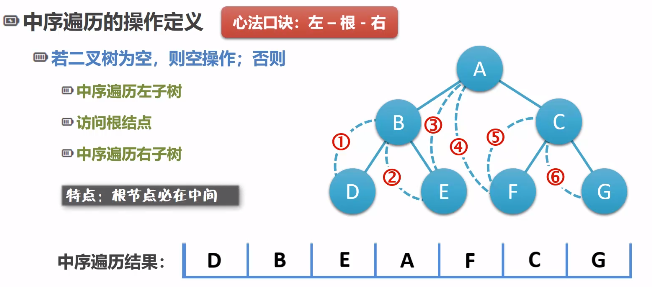
知道先序遍历和后序遍历的结果可以确定树的根结点，但是无法划分左右树。

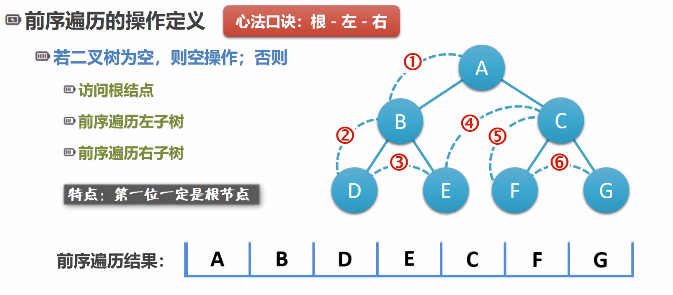
前序遍历

中序遍历

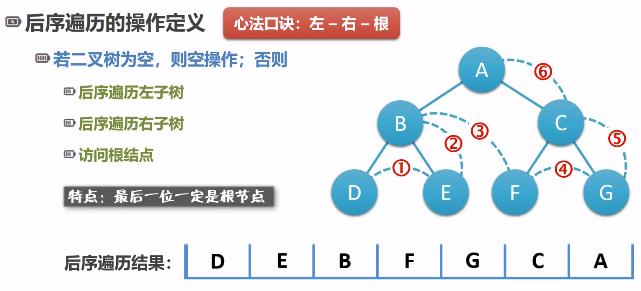
后序遍历

线索二叉树

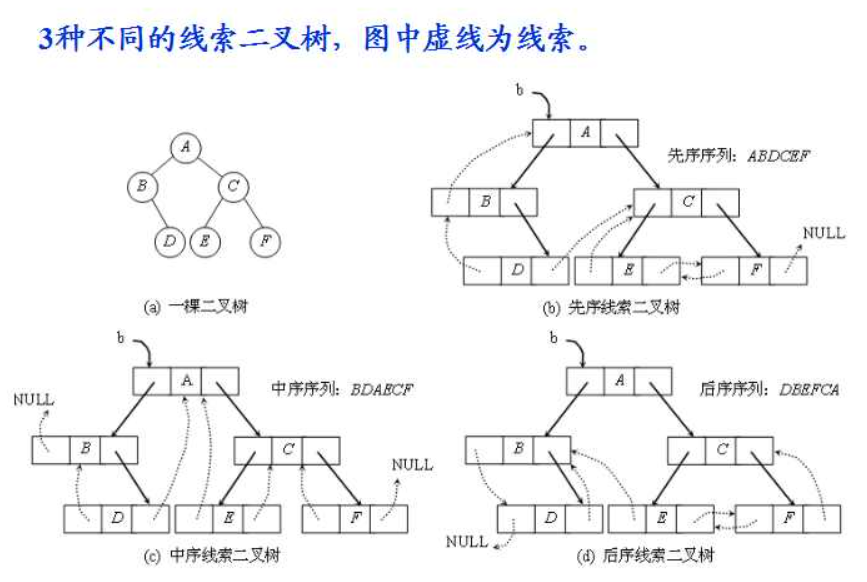
在建立二叉树时就记录下前驱后继的关系，在寻找前驱结点和后继结点时提升效率。

线索化

现将某结点的空指针域指向该结点的前驱后继，定义规则如下：

• 若结点的左子树为空，则该结点的左孩子指针指向其前驱结点。
• 若结点的右子树为空，则该结点的右孩子指针指向其后继结点。

这种指向前驱和后继的指针称为线索。将一棵普通二叉树以某种次序遍历，并添加线索的过程称为线索化。

可以看出通过线索化，既解决了空间浪费问题，又解决了前驱后继的记录问题。

线索化带来新问题

• lchild指向其左子树，若无左子树指向前驱结点
• rchild指向其右子树，若无右子树指向后继结点

  如何区分其 lchild 的指向的结点 J 是其左孩子还是前驱结点？

为了解决这一问题，现需要添加标志位 ltag，rtag。并定义规则如下：

• ltag 为 0 时，指向左孩子，为 1 时指向前驱
• rtag 为 0 时，指向右孩子，为 1 时指向后继

后序线索树的遍历仍需要栈的支持；二叉树线索化后，仍不能有效解决后序线索二叉树中求后序后继。

树的表示法

图像表示法

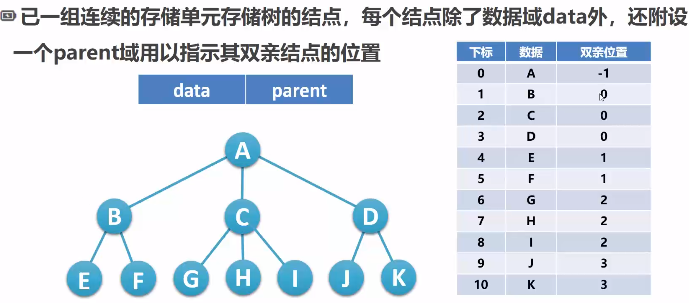
• 双亲表示法
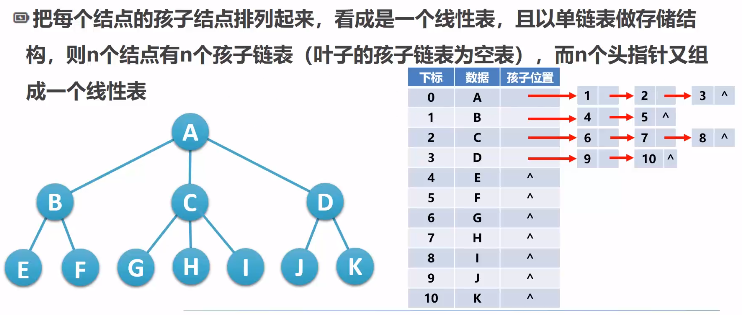
• 孩子表示法
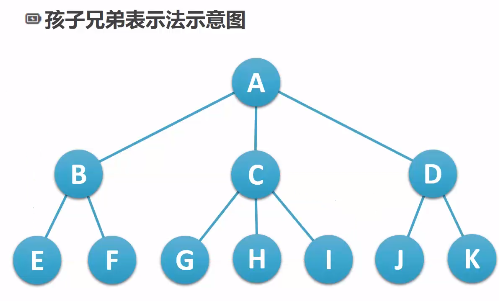
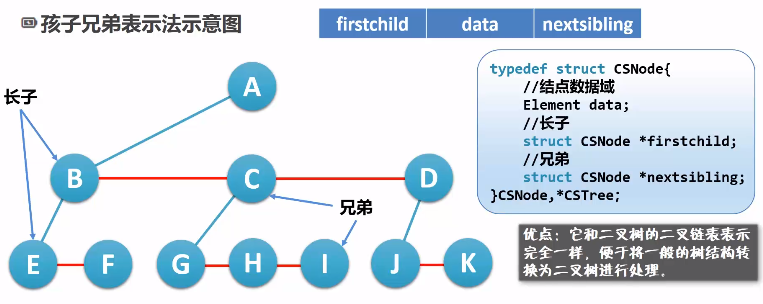
• 孩子兄弟表示法

树、森林与二叉树的转换（易遗忘点）

n个树有n-1条边，每棵树的结点比边多一个。

树转换为二叉树

由于二叉树是有序的，为了避免混淆，对于无序树，我们约定树中的每个结点的孩子结点按从左到右的顺序进行编号。

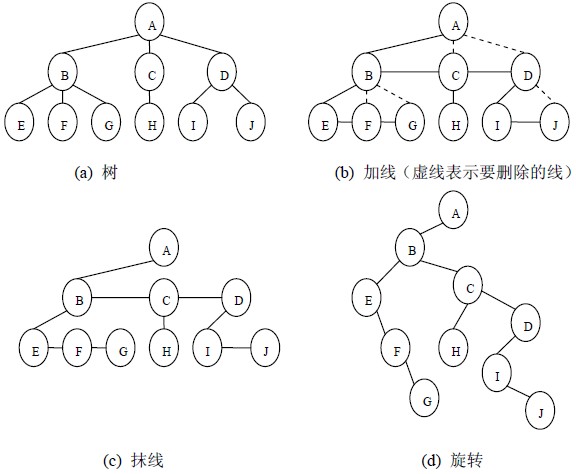
将树转换成二叉树的步骤是：

1. 加线。就是在所有兄弟结点之间加一条连线；
2. 抹线。就是对树中的每个结点，只保留他与第一个孩子结点之间的连线，删除它与其它孩子结点之间的连线；
3. 旋转。就是以树的根结点为轴心，将整棵树顺时针旋转一定角度，使之结构层次分明。

二叉树转换为树

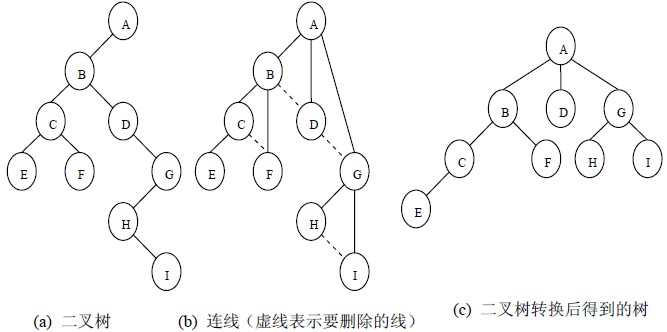
二叉树转换为树是树转换为二叉树的逆过程，其步骤是：

1. 若某结点的左孩子结点存在，将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点，将该结点与这些右孩子结点用线连接起来；
2. 删除原二叉树中所有结点与其右孩子结点的连线；
3. 整理（1）和（2）两步得到的树，使之结构层次分明。

森林转换为二叉树

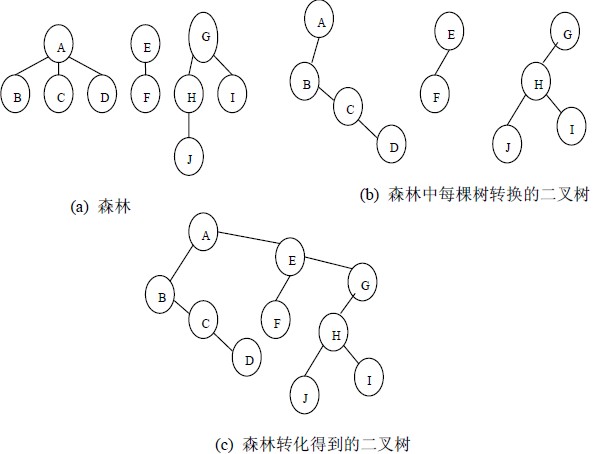
森林是由若干棵树组成，可以将森林中的每棵树的根结点看作是兄弟，由于每棵树都可以转换为二叉树，所以森林也可以转换为二叉树。

将森林转换为二叉树的步骤是：

1. 先把每棵树转换为二叉树
2. 第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子结点，用线连接起来。当所有的二叉树连接起来后得到的二叉树就是由森林转换得到的二叉树。

二叉树转换为森林

二叉树转换为森林比较简单，其步骤如下：

1. 先把每个结点与右孩子结点的连线删除，得到分离的二叉树
2. 把分离后的每棵二叉树转换为树
3. 整理第②步得到的树，使之规范，这样得到森林

总结

根据树与二叉树的转换关系以及二叉树的遍历定义可以推知，树的先序遍历与其转换的相应的二叉树的先序遍历的结果序列相同；树的后序遍历与其转换的二叉树的中序遍历的结果序列相同；树的层序遍历与其转换的二叉树的后序遍历的结果序列相同。由森林与二叉树的转换关系以及森林与二叉树的遍历定义可知，森林的先序遍历和中序遍历与所转换得到的二叉树的先序遍历和中序遍历的结果序列相同。

查并集

并查集是一种树形的数据结构，顾名思义，它用于处理一些不交集的合并及查询问题。 它支持两种操作：

• 查找（Find）：确定某个元素处于哪个子集；
• 合并（Union）：将两个子集合并成一个集合。

也就是说，不支持集合的分离、删除。

参考

【1】树、森林与二叉树的转换