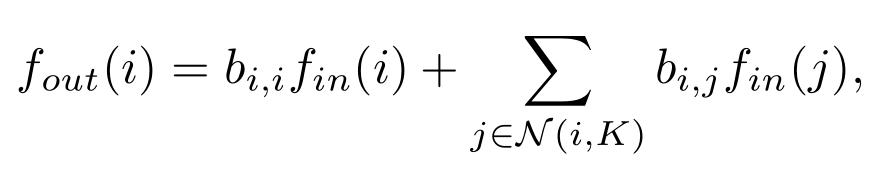谱图理论基础
图信号
图信号可以看作一个作用在图上的函数,在每个顶点上都有一个值。文中用竖线的形式来表示图信号。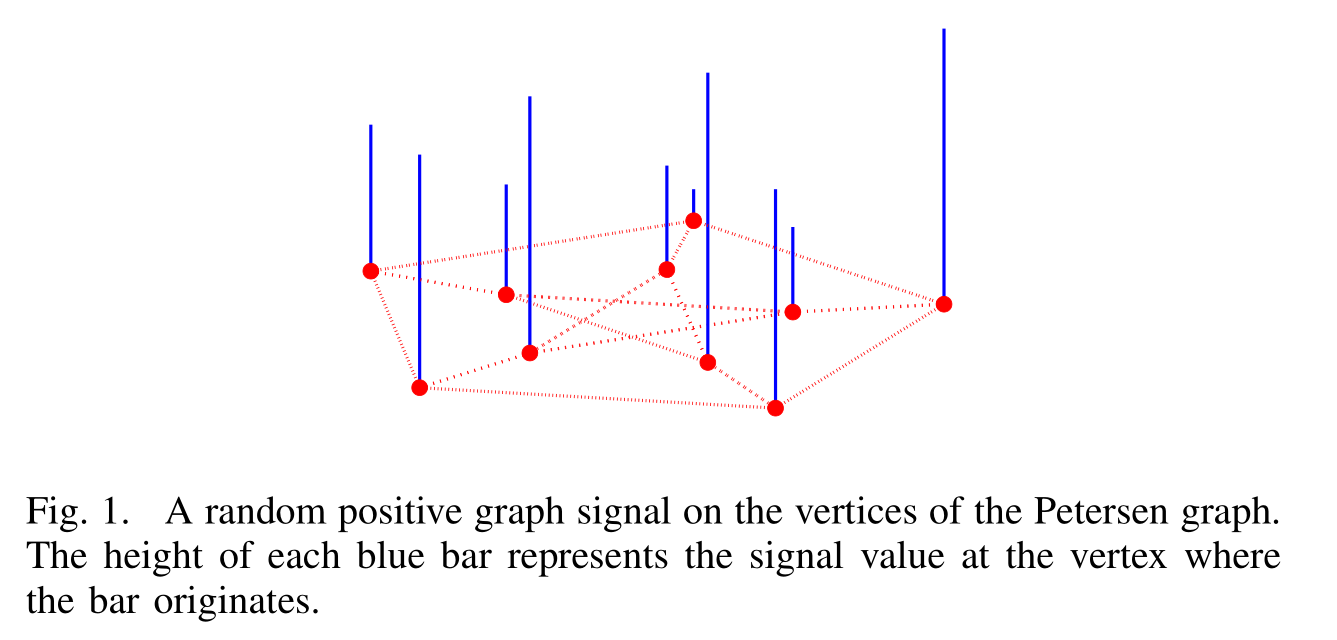
The Non-Normalized Graph Laplacian
非归一化的图 Laplace 矩阵定义为 ,

至于为什么这样定义的 L 可以类比成 Laplace 算子,通俗的解释可以参考《拉普拉斯矩阵与拉普拉斯算子的关系》,严格的证明可看《Discrete Regularization on Weighted Graphs for Image and Mesh Filtering》,也有另一种解释,首先定义梯度: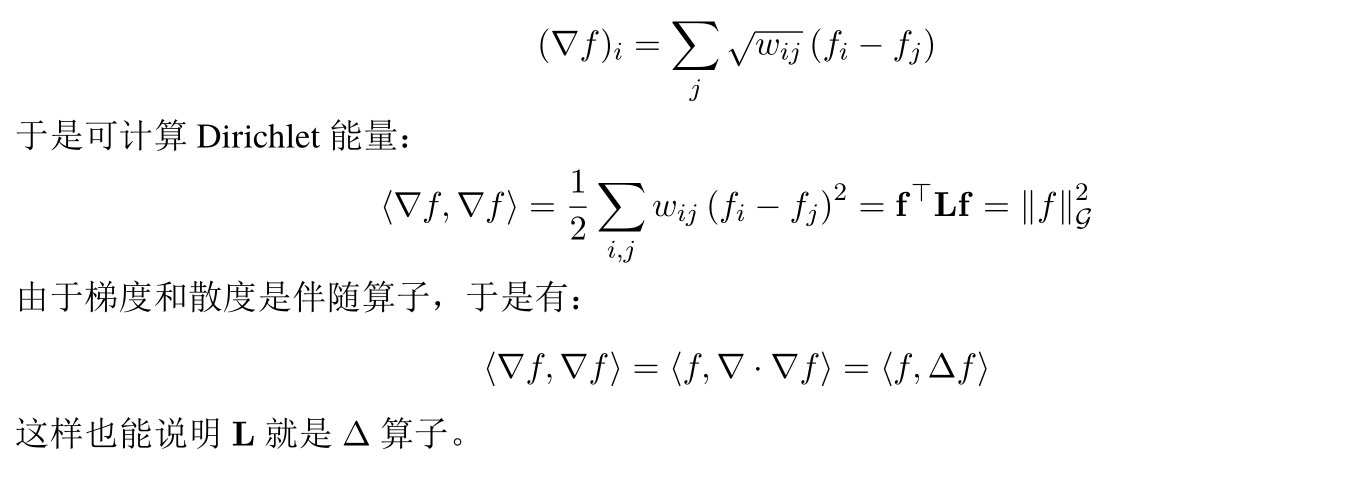
Graph Fourier Transform
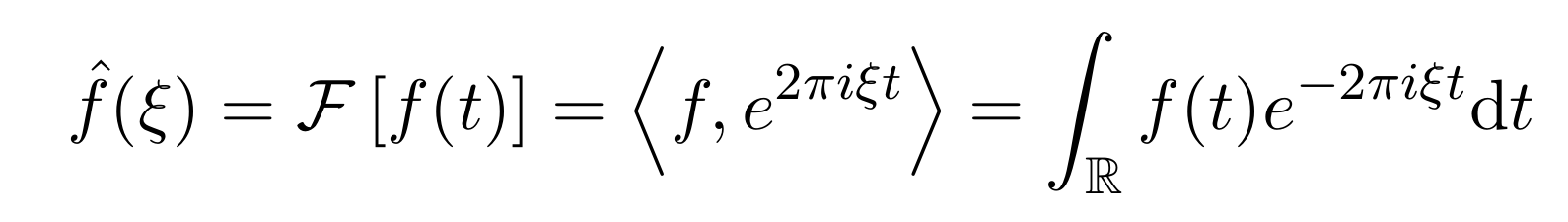 |
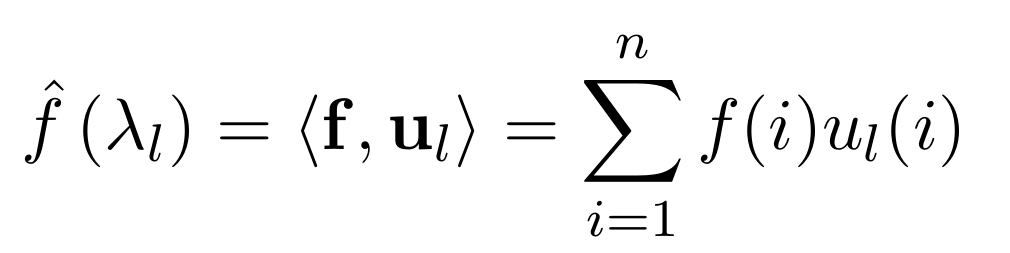 |
|---|---|
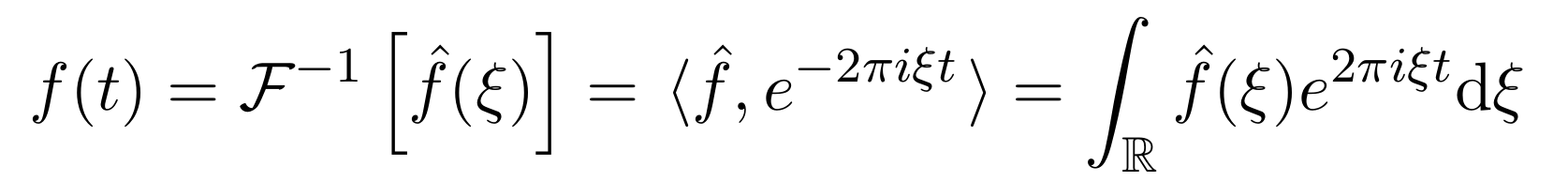 |
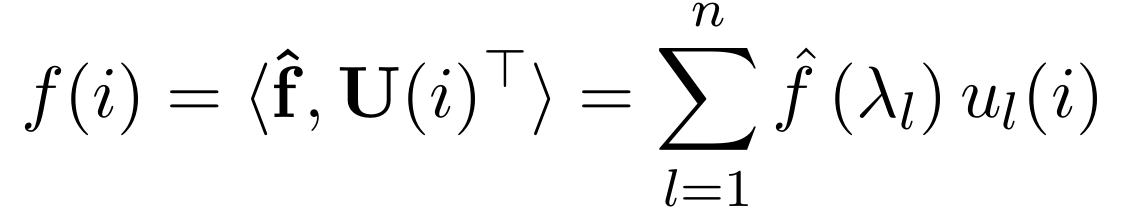 |

特征向量的意义
传统傅里叶变换中的特征值 对应着特征向量的频率:
的绝对值越小,
在 t 上的变化越小。 在图上也有类似的性质:
的绝对值越小,
在 i 上的变化越小。
事实上,当 时,
在同一连通分量顶点上的值都相等。
由此还可引出 Laplace 矩阵的另一个性质:L 的零特征值的重数,等于图中连通分量的个数。
想看证明的可以去翻 Hamilton的 《Graph Representation Learning》第22页。
算了,还是贴上来吧:

扯远了,我们继续,作者设计了一个实验,把特征向量的值在图上可视化了出来,可以看到 上的值几乎都是一样的;
上的值有所变化,但变化很规律,过渡很平滑;而到了
,变化就相当剧烈了。

《Geometric deep learning: going beyond Euclidean data》中也有张类似的图: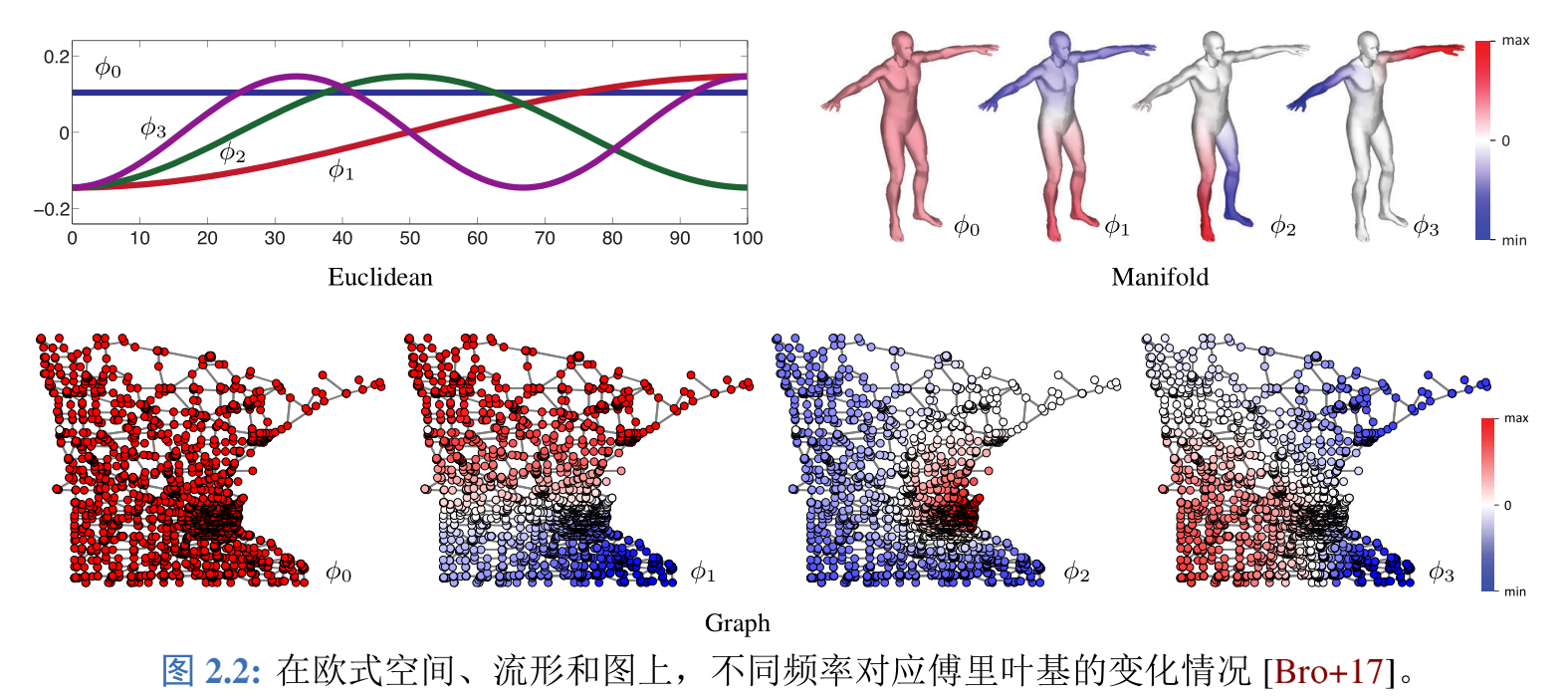
至于如何定量地分析这一现象,论文中也有提及,这一组基也可以从使图信号最光滑的角度来定义:
图上的滤波
谱域滤波
传统信号处理中是这样使用滤波函数的:
其中 就是滤波的变换函数(Transfer function)。
使用卷积公式,在频域做滤波等价于在空域做卷积: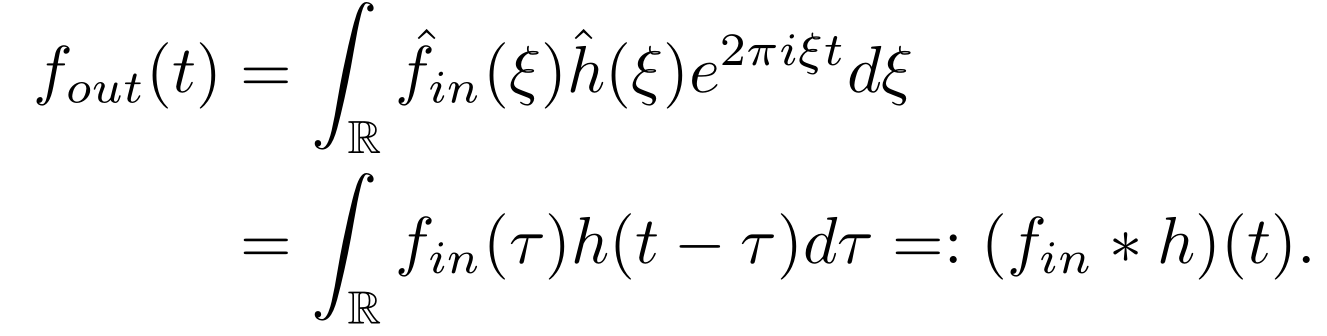
类似的,如果我们要在图上的谱域做滤波:
其傅里叶逆变换为:
矩阵形式推导如下:
空域滤波
二者之间的联系
如果谱域滤波的变换函数为 K 阶多项式:
那么有: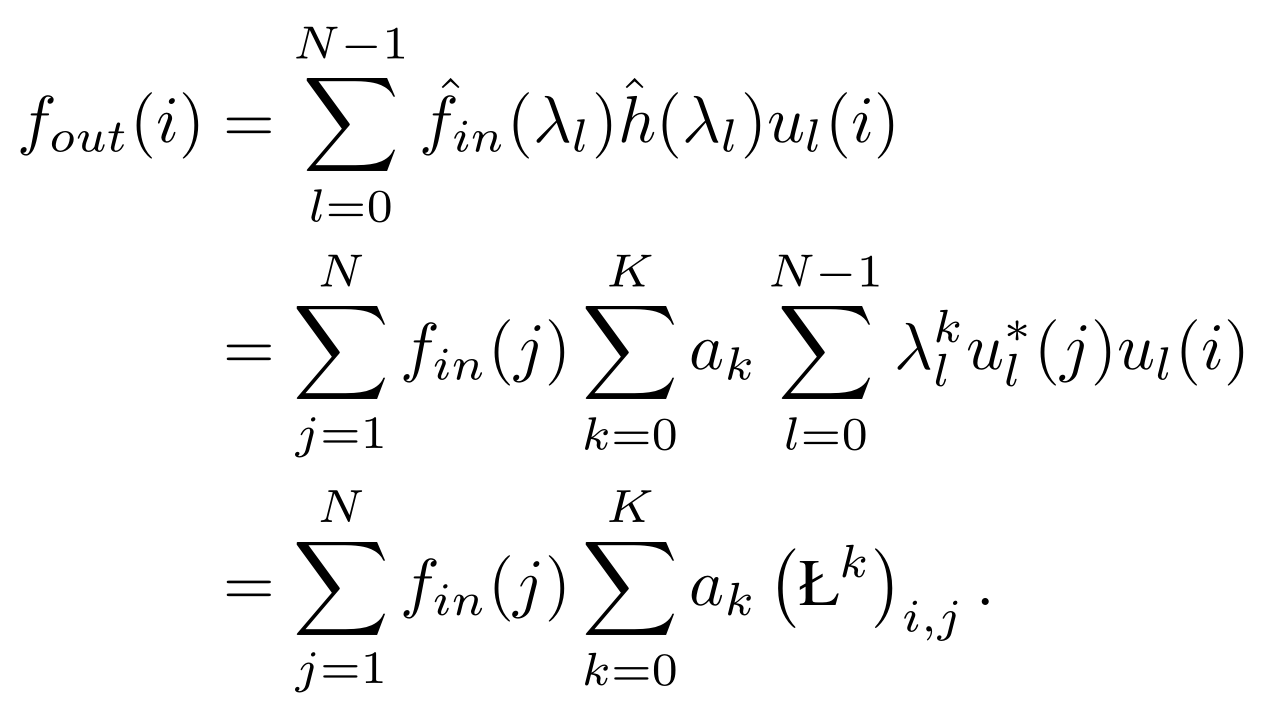
原论文的写法有点让人头晕,写成矩阵形式就很好理解了:
这样两者就联系起来了: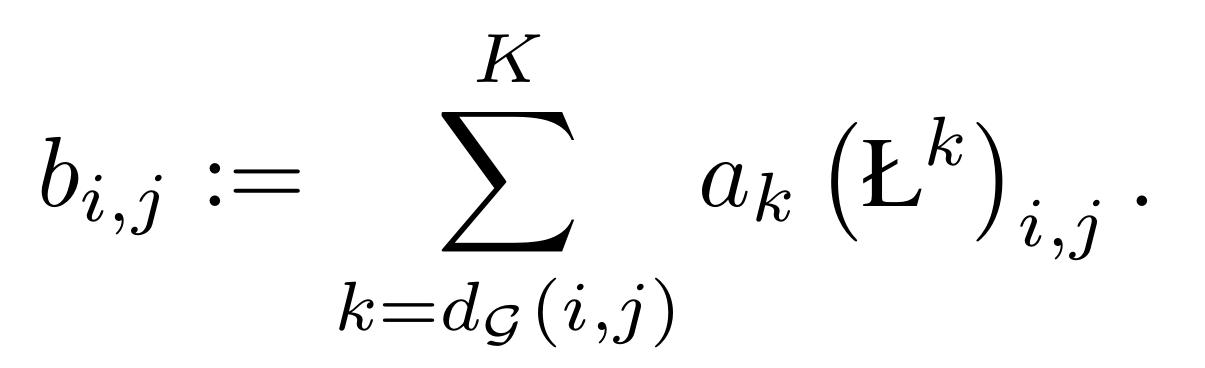
有一点需要注意的是,如果 ,那么说明 i 和 j 之间的最短路长度
,这一点和邻接矩阵的性质一样,证明见《Wavelets on graphs via spectral graph theory》的 Lemma 5.4,贴个证明懒得再翻了。

其他内容
还有一些内容似乎暂时用不上,就没看了,有空再填坑。