Geodesic CNN

Title

摘要

在极坐标下定义了一种流形上的卷积算子，网络由滤波器、线性和非线性算子的级联组成，其系数为可学习参数。

Background

流形上的LB算子，其特征函数构成了流形上的一组正交基。

流形上的热扩散方程，其解为各点传递过来的热量之和。

三角网格上的LB算子

Spectral descriptors

主流的谱描述子都是通过谱域上的transfer function来实现的.

Convolutional neural networks on manifolds

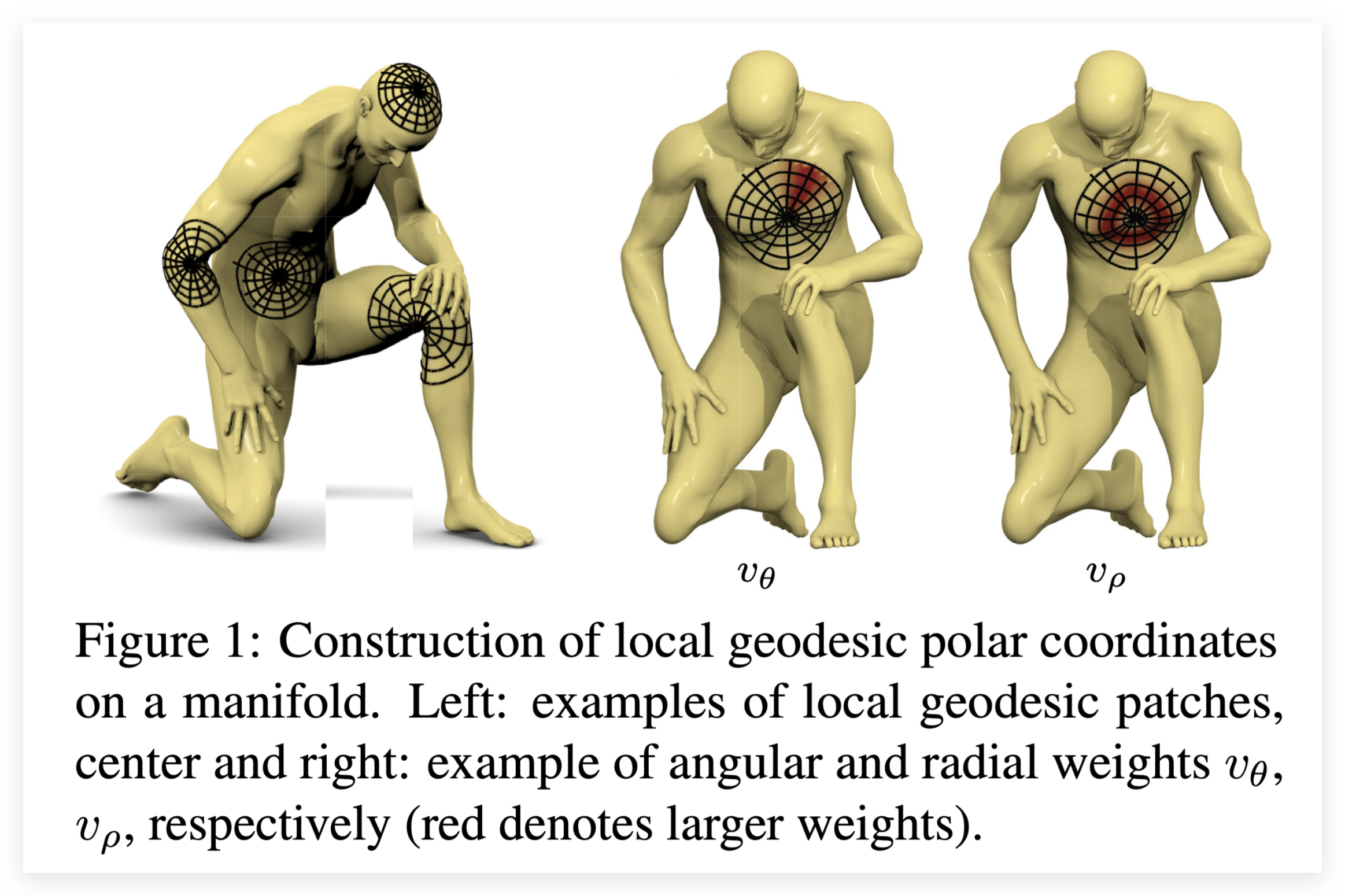
Geodesic convolution

这里先介绍 Patch 算子，计算了f在点x处附近一个patch中的加权和。
看起来有点复杂，可以把它类比于图像上的高斯滤波算子，不同的是，高斯滤波的权值随欧式距离衰减，而patch算子的权值随经度和维度的差异之积衰减。

将f映射成了一个极坐标系下的函数，是定义在极坐标系上的一个滤波函数。
那么f和a在流形上的卷积通过极坐标系下的乘积表示。

为什么要这样定义呢？因为空间上的卷积都可以通过和卷积核的乘积表示，但需要将卷积窗口的大小和卷积核的尺寸对齐，因此考虑到转化到极坐标系下。

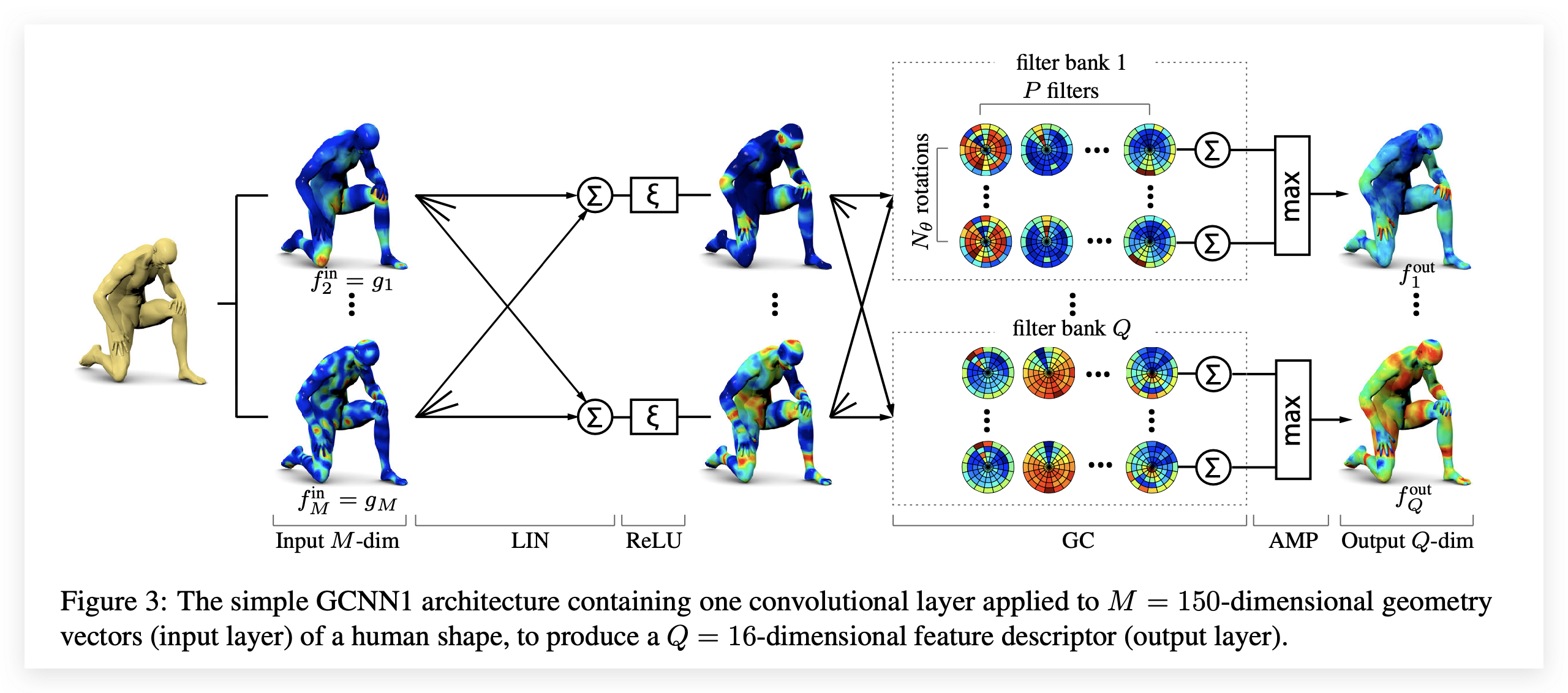
Geodesic CNN

线性层就是输入特征的线性组合

卷积层，为了保证由不同角度建立的极坐标系下得到的值都相同，因此做卷积时就将所有角度都卷一遍。

最大值池化层，同样考虑到角度的不变性，采用所有角度中的最大值。

计算不同角度w在傅里叶变换后的系数。

最后摆一个整体架构。