简介

我们将多项式系数作为可训练的参数，即定义Chebyshev Spectral CNN - 图1#card=math&code=g_%7B%5Ctheta%7D%5Cleft%28%20%5Cmathbf%7B%5CLambda%20%7D%20%5Cright%29&id=rtgjw) 为：

Chebyshev Spectral CNN - 图2%20%3D%5Csum%7Bk%3D0%7D%5EK%7B%5Ctheta_k%5Cmathbf%7B%5CLambda%20%7D%5Ek%7D%0A#card=math&code=g%7B%5Ctheta%7D%5Cleft%28%20%5Cmathbf%7B%5CLambda%20%7D%20%5Cright%29%20%3D%5Csum_%7Bk%3D0%7D%5EK%7B%5Ctheta_k%5Cmathbf%7B%5CLambda%20%7D%5Ek%7D%0A&id=h3A93)

卷积操作写作：

Chebyshev Spectral CNN - 图3

这样的话就保证了空间局部性，将训练参数的量级从 Chebyshev Spectral CNN - 图4#card=math&code=%5Cmathcal%7BO%7D%28n%29&id=hTm6B) 变成了 Chebyshev Spectral CNN - 图5#card=math&code=%5Cmathcal%7BO%7D%28K%29&id=WmoQX)，并且也避免了对矩阵 Chebyshev Spectral CNN - 图6 的显式特征分解。

ChebNet 提出用 Chebyshev 多项式来替换一般多项式，即定义 Chebyshev Spectral CNN - 图7#card=math&code=g_%7B%5Ctheta%7D%28%20%5Cmathbf%7B%5Ctilde%7B%5CLambda%7D%20%7D%20%29&id=rJcyi) 为：

Chebyshev Spectral CNN - 图8%20%3D%5Csum%7Bk%3D0%7D%5EK%7B%5Ctheta%20_k%20%5Cmathbf%7BT%7D_k(%20%5Cmathbf%7B%5Ctilde%7B%5CLambda%7D%20%7D%20)%7D%0A#card=math&code=g%7B%5Ctheta%7D%28%20%5Cmathbf%7B%5Ctilde%7B%5CLambda%7D%20%7D%20%29%20%3D%5Csum_%7Bk%3D0%7D%5EK%7B%5Ctheta%20_k%20%5Cmathbf%7BT%7D_k%28%20%5Cmathbf%7B%5Ctilde%7B%5CLambda%7D%20%7D%20%29%7D%0A&id=J7jmi)

卷积操作写作：

Chebyshev Spectral CNN - 图9%5Cmathbf%7Bx%7D%0A#card=math&code=%5Clabel%7Beq%3Achev%7D%0A%20%20%20%20%5Cmathbf%7Bg%7D%7B%5Ctheta%7D%5Cstar%20%5Cmathbf%7Bx%7D%3D%20%5Csum%7Bk%3D0%7D%5EK%7B%5Ctheta%20_k%7D%5Cmathbf%7BT%7D_k%28%5Cmathbf%7B%5Ctilde%7BL%7D%7D%29%5Cmathbf%7Bx%7D%0A&id=J7E8W)

其中 Chebyshev Spectral CNN - 图10 ，该操作的目的是将 Chebyshev Spectral CNN - 图11 的最大特征值约束到 Chebyshev Spectral CNN - 图12，因为 Chebyshev 多项式的定义域在Chebyshev Spectral CNN - 图13上。注意这里的Chebyshev Spectral CNN - 图14 为归一化 Laplace 矩阵，特征值范围为 Chebyshev Spectral CNN - 图15。

Chebyshev 多项式的初项为 Chebyshev Spectral CNN - 图16%3D1%2C%5C%2C%5Cmathrm%7BT%7D%7B1%7D(x)%3Dx#card=math&code=%5Cmathrm%7BT%7D%7B0%7D%28x%29%3D1%2C%5C%2C%5Cmathrm%7BT%7D_%7B1%7D%28x%29%3Dx&id=Fh34z)， 后面项由递推式定义：

Chebyshev Spectral CNN - 图17%3D2x%5Cmathrm%7BT%7D%7Bk-1%7D(x)-%5Cmathrm%7BT%7D%7Bk-2%7D(x)%2C%5Cquad%0A#card=math&code=%5Cmathrm%7BT%7Dk%28x%29%3D2x%5Cmathrm%7BT%7D%7Bk-1%7D%28x%29-%5Cmathrm%7BT%7D_%7Bk-2%7D%28x%29%2C%5Cquad%0A&id=I225k)

令 Chebyshev Spectral CNN - 图18%5Cmathbf%7Bx%7D%2C%5Cquad%5Cmathbf%7B%5Cbar%7Bx%7D%7D_0%3D%5Cmathbf%7Bx%7D%2C%5C%2C%5Cmathbf%7B%5Cbar%7Bx%7D%7D_1%3D%5Cmathbf%7B%5Ctilde%7BL%7Dx%7D#card=math&code=%5Cmathbf%7B%5Cbar%7Bx%7D%7D_k%3D%5Cmathbf%7BT%7D_k%28%5Cmathbf%7B%5Ctilde%7BL%7D%7D%29%5Cmathbf%7Bx%7D%2C%5Cquad%5Cmathbf%7B%5Cbar%7Bx%7D%7D_0%3D%5Cmathbf%7Bx%7D%2C%5C%2C%5Cmathbf%7B%5Cbar%7Bx%7D%7D_1%3D%5Cmathbf%7B%5Ctilde%7BL%7Dx%7D&id=gddZP)，然后可通过递推计算：

Chebyshev Spectral CNN - 图19

那么卷积操作可写成 Chebyshev Spectral CNN - 图20，由于 Chebyshev Spectral CNN - 图21 是稀疏矩阵，计算复杂度可降到 Chebyshev Spectral CNN - 图22#card=math&code=%5Cmathcal%7BO%7D%28mK%29&id=unr2I)。

:::danger 为什么要用 Chebyshev 多项式来代替一般多项式？ ::: 很多文章说是用递推的方式可以节省计算量，但实际上传统多项式相当于把 Chebyshev Spectral CNN - 图23 替换成 Chebyshev Spectral CNN - 图24，两者计算复杂度是一模一样的。而原论文也没有提到相比于传统多项式， Chebyshev 多项式的优势在哪。 我上网找了很多关于这篇论文的解读，都没有解释清楚这个问题，最后终于在 GitHub 的讨论区 《Why the Chebyshev polynomials is needed?》 找到了答案：作者很诚实地回复说其实没啥区别。。。

Fast Pooling of Graph Signals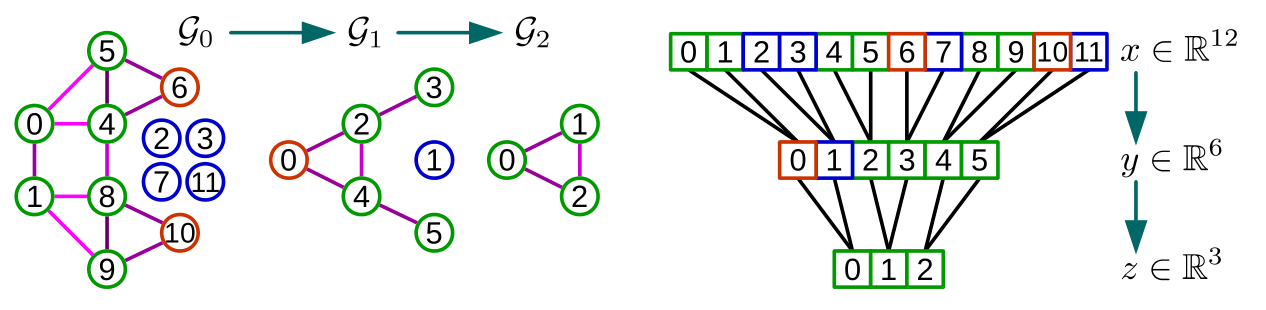
image.png
这张图看起来比较迷惑，我画成另一个样子应该就比较直观了。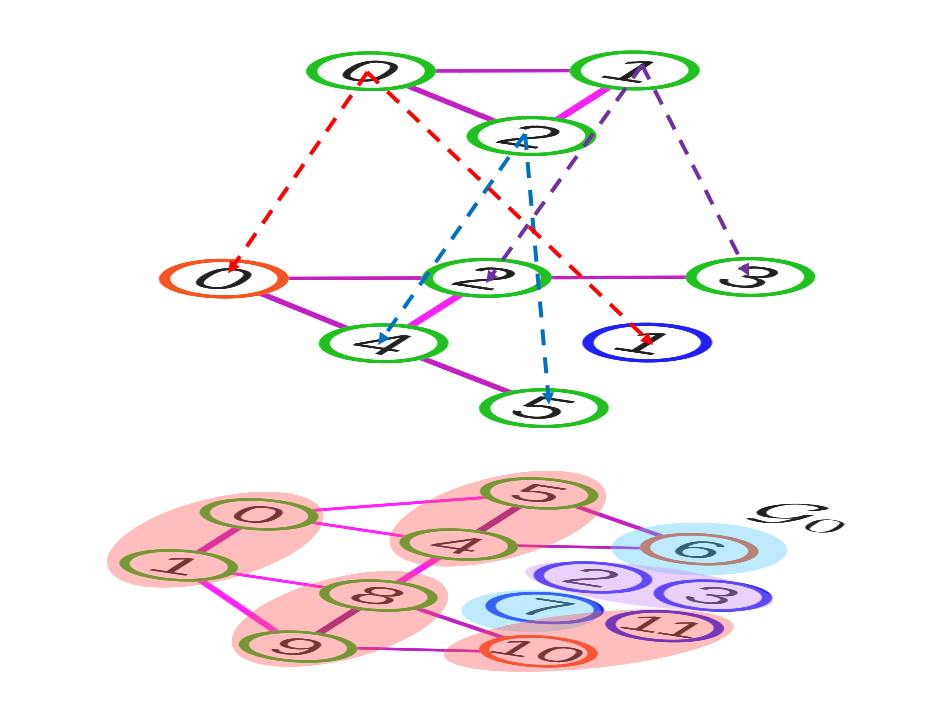
image.png

参考

  1. 《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》
  2. paper8：CNN On Graphs With Spectal Filtering