AGCN

简介

标题

《Adaptive Graph Convolutional Neural Networks》

概述

作者认为在传统 GCN 中，图中节点的关系仅仅由邻接矩阵表示是不够的，节点和节点之间存在着大量的隐式关系。因此作者通过学习一个残差邻接矩阵来表示这种隐式关系。

小记

Residual Graph Laplacian

用残差矩阵 来学习隐式关系，最终使用的 Graph Laplacian 则是原来的Laplace 矩阵加上残差矩阵：

Distance metric learning

从算法图中可以看出，残差矩阵由隐式邻接矩阵 决定，而邻接矩阵衡量的是相关性。
节点之间的相关性，不仅仅体现在图结构上，也体现在节点特征之间的相似性。
作者认为仅仅用欧式距离不足以度量相似性，因此选择 GeneralizedMahalanobis distance：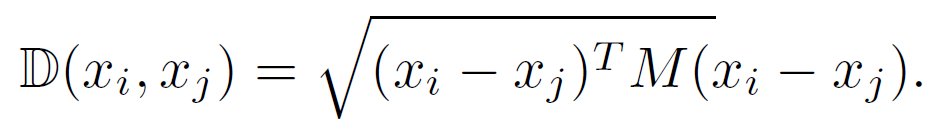

是个对称半正定矩阵，就是要学习的参数。

Dense adjacency matrix

作者使用高斯核函数将距离转化为密度：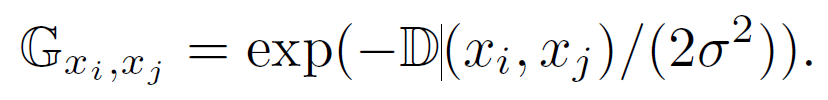

将密度矩阵归一化之后，便是隐式邻接矩阵 。