【数据结构与算法基础】代码仓库:https://github.com/jinrunheng/datastructure-and-algorithm
一:集合基础
什么是集合?
集合(Set)是基本的数学概念,指的是具有某种特定性质的事物的总体。
集合有以下几种特性:
- 无序性
一个集合中,每个元素的地位都是相同的,元素之间是无序的
- 互异性
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次
- 确定性
给定一个集合,任意一个元素。该元素只存在属于或不属于该集合两种情况,不允许有模棱两可的情况出现
二:基于二分搜索树的集合实现
我们可以使用我们自己的二分搜索树来实现集合,因为我们的二分搜索树不支持插入重复的元素,所以使用它作为底层也符合集合的互异性。
三:基于链表的集合实现
同样地,我们也可以使用我们自己的链表来实现集合,不过在添加元素时,我们需要判断添加的元素是否在当前链表中已经存在,如果没有存在则可以添加,如果已存在则不能添加。
四:集合的复杂度分析
测试
对于我们实现的 BSTSet(基于二分搜索树的集合实现)与 LinkedListSet(基于链表的集合实现)二者性能有多大的差异?我们来具体测试一下:
package com.github.datastructureandalgorithm.datastructure.Set;import org.junit.jupiter.api.Test;import java.util.ArrayList;import java.util.List;import java.util.UUID;public class SetPerformanceTest {private static List<String> generateTestList() {List<String> list = new ArrayList<>();for (int i = 0; i < 100000; i++) {String s = UUID.randomUUID().toString();list.add(s);if (i % 3 == 0) {list.add(list.get(list.size() - 1));}}return list;}private static double testSet(Set<String> set, List<String> strings) {long startTime = System.nanoTime();for (String s : strings) {set.add(s);}long endTime = System.nanoTime();return (endTime - startTime) / 1000000000.0;}@Testvoid performanceTest() {List<String> strings = generateTestList();BSTSet<String> bstSet = new BSTSet<>();LinkedListSet<String> linkedListSet = new LinkedListSet<>();double time1 = testSet(bstSet, strings);System.out.println("BST Set : " + time1 + " s");double time2 = testSet(linkedListSet, strings);System.out.println("LinkedList Set : " + time2 + " s");}}
代码很简单,在这里就不过多说明了;对于十万这个量级的数据,我的电脑运行测试结果如下:
BST Set : 0.129656602 sLinkedList Set : 28.116667089 s
可以看到,二者的差异是巨大的。
复杂度分析
对于底层为链表的集合来说,添加,查找,删除元素的时间复杂度均为 ,而底层为二分搜索树的集合则不同,让我们回想一下向二分搜索树中添加元素的逻辑:
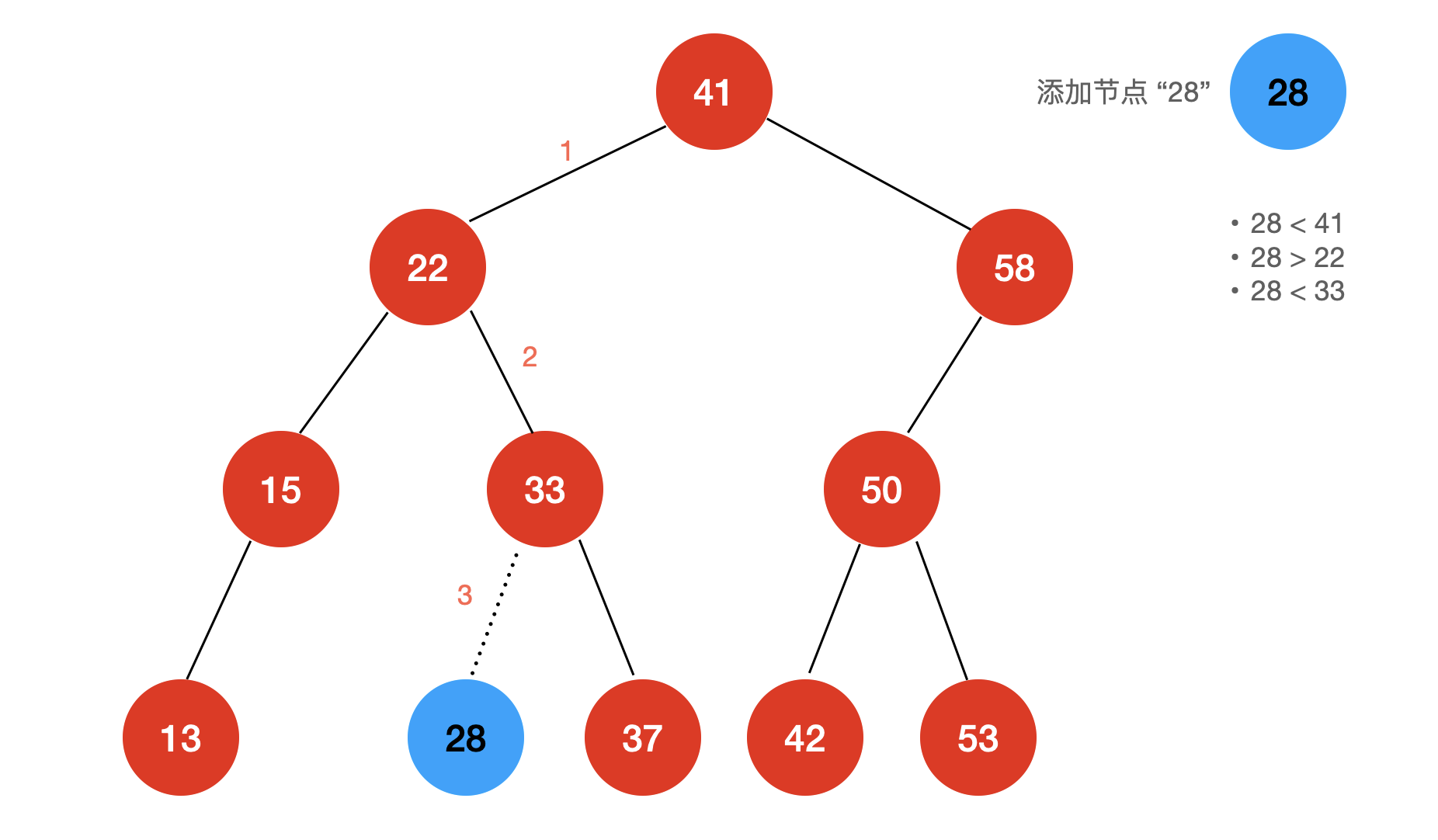
与链表不同,向二分搜索树中添加一个元素,最多只需要走这棵树的“高度”或“深度”。在这里我们使用“高度”这个词来描述。我们将二叉树的高度记作 h,很显然,对于底层为二分搜索树的集合来说,添加,查找,删除元素的时间复杂度均为 。
h 与 N 的关系是怎样的呢?
当一棵二叉树为满二叉树时,h 与 N 满足关系式: 即:,所以,此时对于底层为二分搜索树的集合来说,它的增,删,查找的时间复杂度为:
不过, 这个时间复杂度是我们考虑的最优的情况,如果我们的二分搜索树的节点分布“均衡”,时间复杂度自然是 ;可是如果出现了最差的情况,二分搜索树就会退化为一个链表:
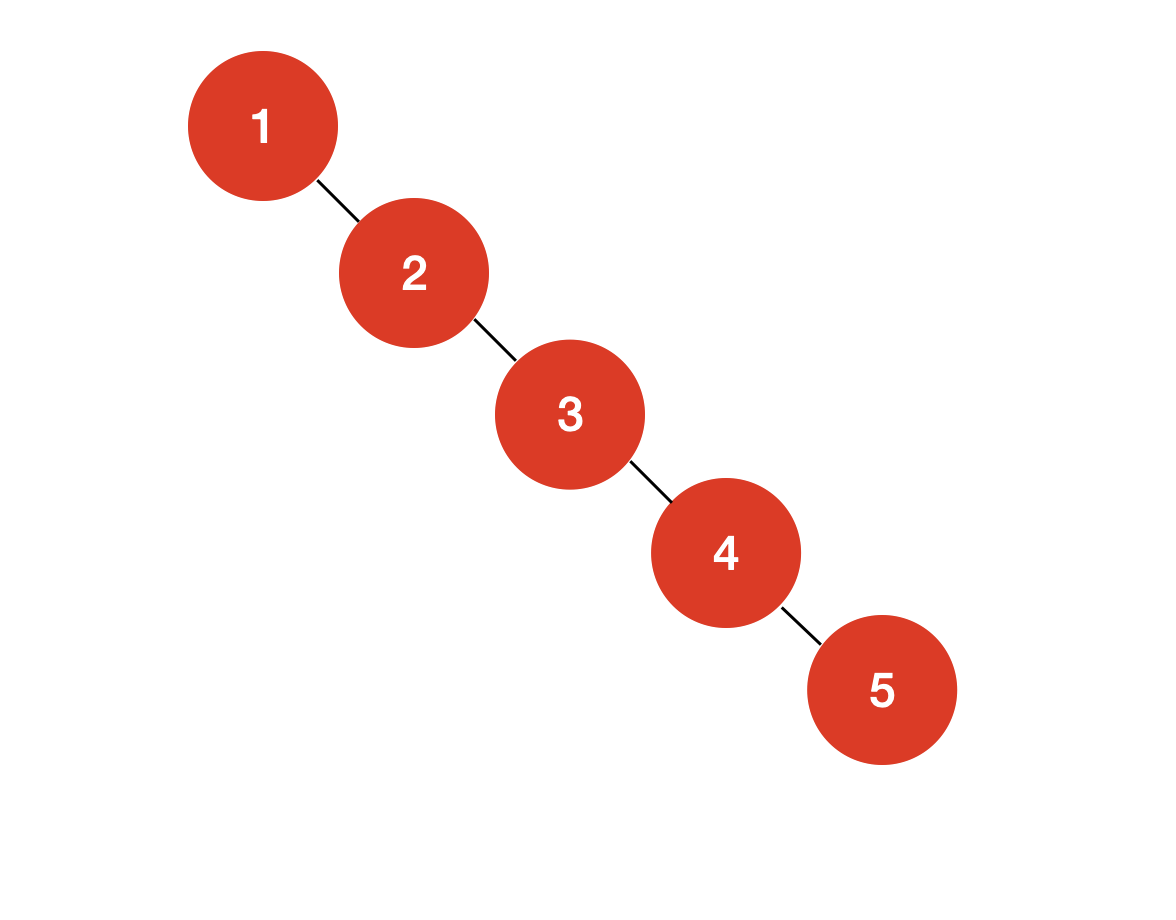
而此时,这棵二分搜索树与链表无异,增,删,查找的时间复杂度将退化为 。
复杂度:
| LinkedListSet | BSTSet(平均) | BSTSet(最差) | |
|---|---|---|---|
| add | O(N) | O(logN) | O(N) |
| contains | O(N) | O(logN) | O(N) |
| remove | O(N) | O(logN) | O(N) |
五:映射基础
映射(Map)指的是两个元素的集合之间元素相互“对应”的关系。在数学及相关的领域等同于函数。
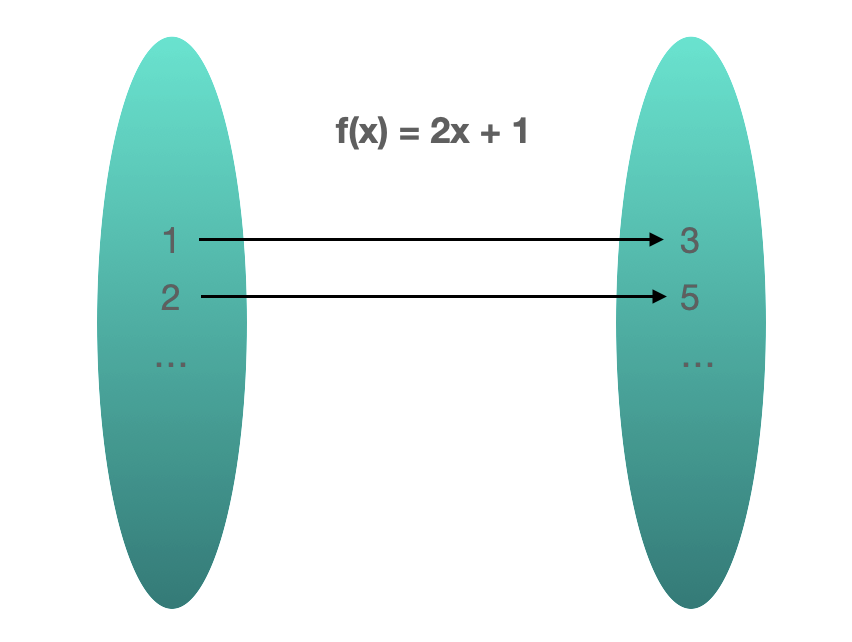
映射的基本概念:
- 映射是一种以键值对形式存储的数据结构(key,value)
- 映射可以根据键(key),寻找值(value)
- 映射中,键是唯一的,一个值可能对应多个键,但是一个键只能对应一个值。
六:基于链表的映射实现
以链表作为底层数据结构实现映射。
七:基于二分搜索树的映射实现
以二分搜索树作为底层数据结构实现映射。
八:映射的复杂度分析
测试
为了观察我们实现的 BSTMap(基于二分搜索树的映射实现)与 LinkedListMap(基于链表的映射实现)二者性能的差异,我们使用代码进行测试:
package com.github.datastructureandalgorithm.datastructure.Map;import org.junit.jupiter.api.Test;import java.util.ArrayList;import java.util.List;import java.util.Random;import java.util.UUID;public class MapPerformanceTest {private static List<String> generateTestList() {List<String> list = new ArrayList<>();for (int i = 0; i < 100000; i++) {String s = UUID.randomUUID().toString();list.add(s);if (i % 3 == 0) {int random = new Random().nextInt(list.size());list.add(list.get(random));}}return list;}private static double testMap(Map<String, Integer> map, List<String> list) {long startTime = System.nanoTime();for (String word : list) {if (map.contains(word)) {map.set(word, map.get(word) + 1);} else {map.add(word, 1);}}long endTime = System.nanoTime();return (endTime - startTime) / 1000000000.0;}@Testvoid performanceTest() {LinkedListMap<String, Integer> linkedListMap = new LinkedListMap<>();BSTMap<String, Integer> bstMap = new BSTMap<>();List<String> words = generateTestList();double time1 = testMap(linkedListMap, words);System.out.println("LinkedListMap : " + time1 + " s");double time2 = testMap(bstMap, words);System.out.println("BSTMap : " + time2 + " s");}}
对于十万这个量级的数据,我的电脑运行测试结果如下:
LinkedListMap : 84.925896898 sBSTMap : 0.163672168 s
复杂度分析
上面的测试结果差异之大,究其原因,和我们上面用链表与二分搜索树实现集合分析的结果是一样的。BSTMap 平均下来看,整体的时间复杂度为 ,而 LinkedListMap 所有操作的时间复杂度均为 。
| LinkedListMap | BSTMap(平均) | BSTMap(最差) | |
|---|---|---|---|
| add | O(N) | O(logN) | O(N) |
| remove | O(N) | O(logN) | O(N) |
| set | O(N) | O(logN) | O(N) |
| get | O(N) | O(logN) | O(N) |
| contains | O(N) | O(logN) | O(N) |



