【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：什么是线段树

线段树（Segment Tree），是 1977 年由 Jon Louis Bentley 发明的一种数据结构，用以存储区间或线段，并且允许快速查询结构内包含某一点的所有区间。

线段树主要用于区间内的查询和统计，例如，我们有如下数组：

image.png
如果我们查询区间 [n,m] 的最大值，最小值或者是这个区间的数字和，很显然，对于数组这样的线性数据结构来说时间复杂度为 O(N)。

我们可以将这个数组构建成一棵线段树：

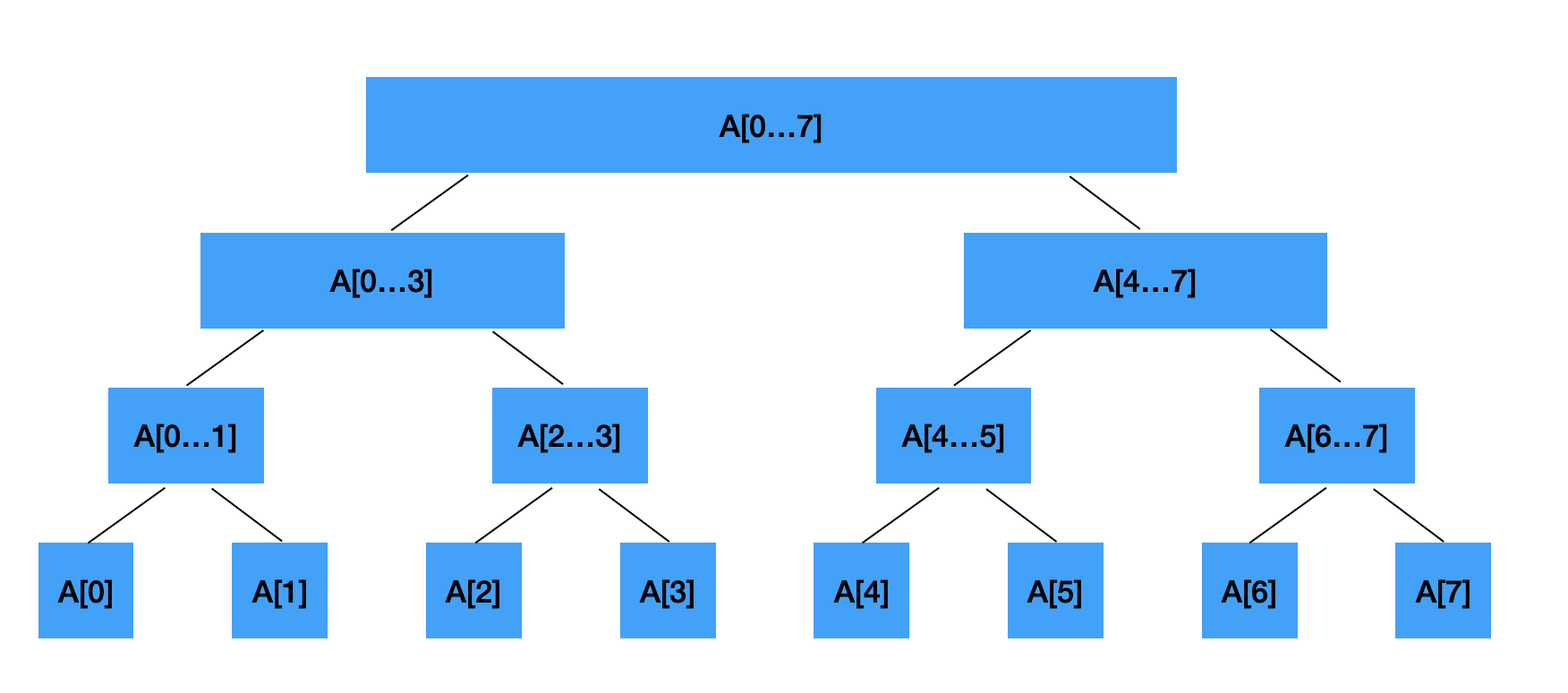
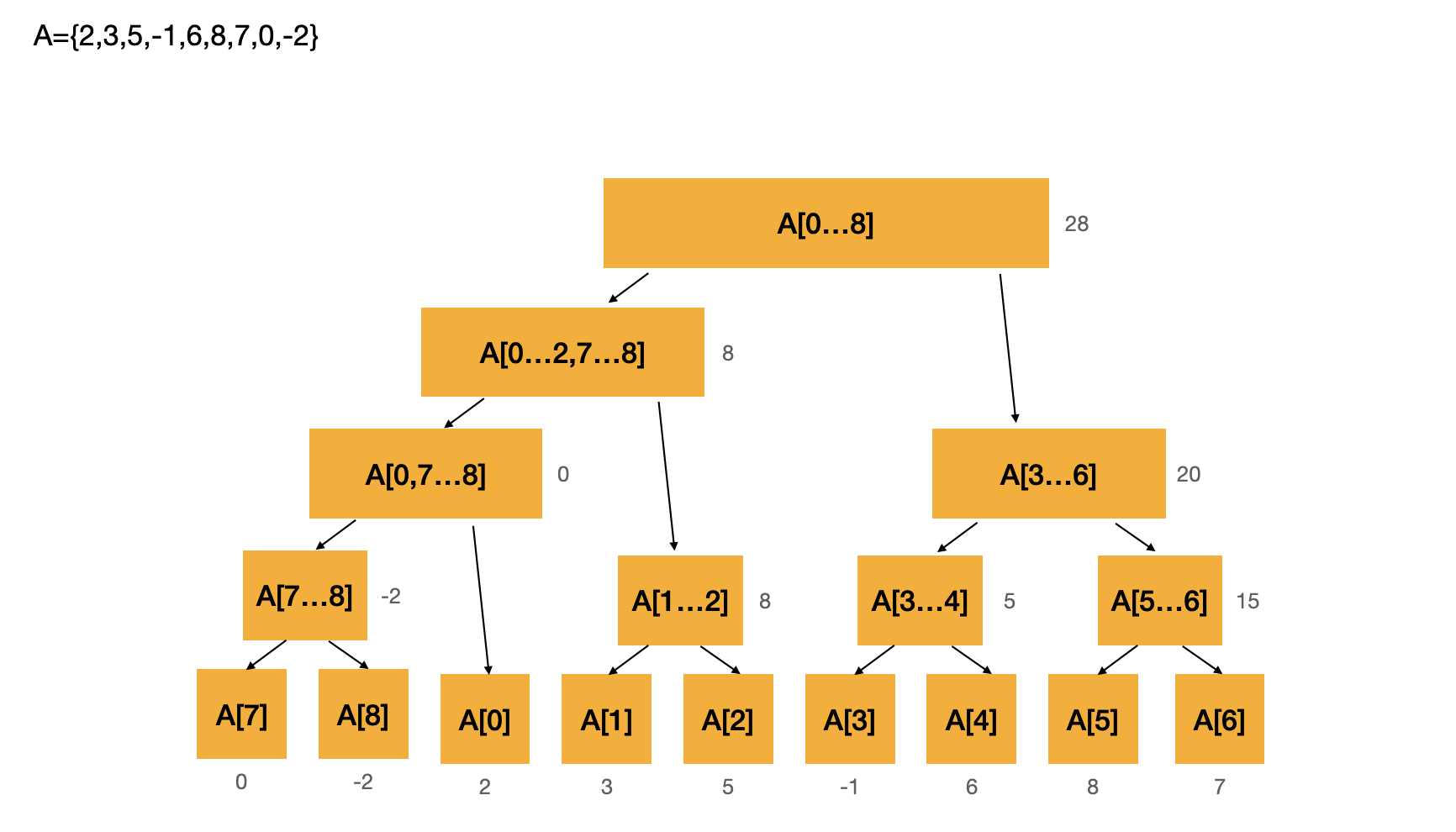
image.png
线段树的每一个节点存储着一段区间的信息，譬如我们的需求为查询 [n,m] 这个区间的数字和，那么线段树的节点存储的就是某个区间数字和的信息。

如果我们要查询 [2,5] 这个区间的数字和

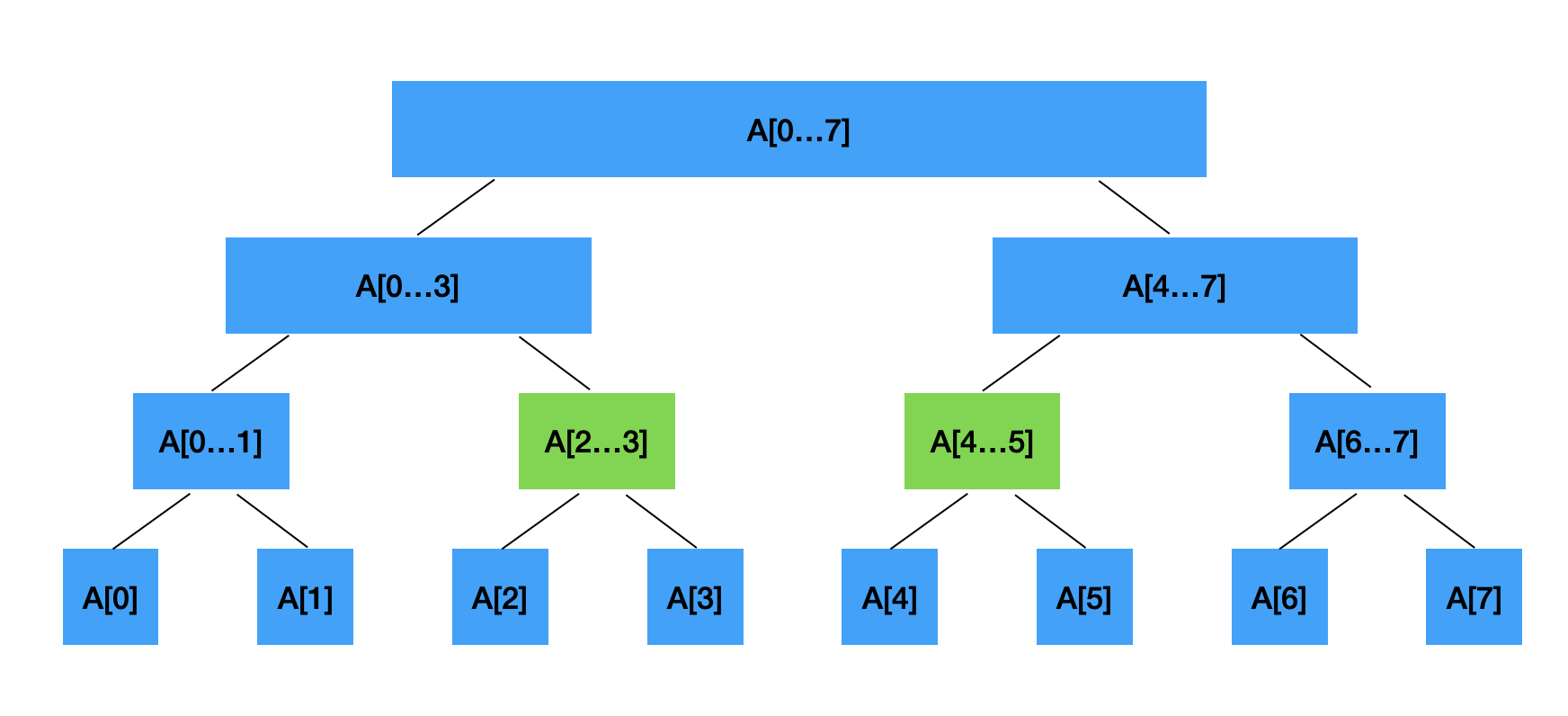
image.png
使用线段树这种数据结构，我们就可以快速获取到我们需要查询的区间信息。

二：线段树的基础表示

线段树是一棵平衡二叉树（Balanced Binary Tree），平衡二叉树具有的性质为：树的最大深度与最小深度的高度差不超过 1

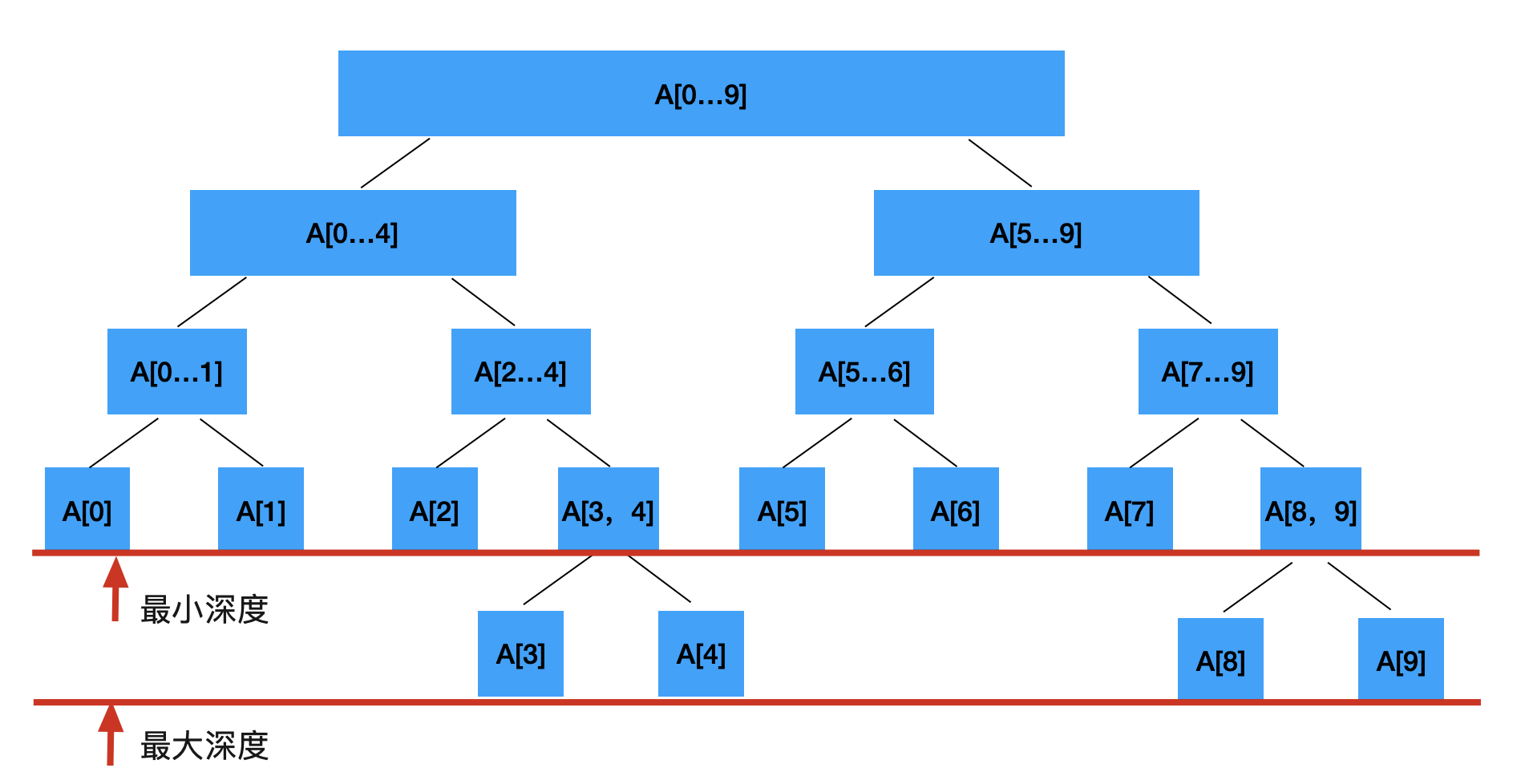
image.png

所以，对于线段树查找的时间复杂度为 O(logN)。

那么，如果数组中有 n 个元素，将这个数组表示为线段树的话，一共需要构建多少个节点呢？

如果，n 满足：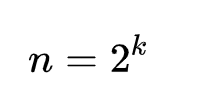
image.png
我们需要开辟 2n 的空间去构建线段树；

否则，n 满足：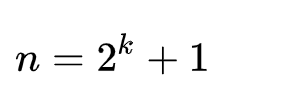
image.png
我们就需要开辟 4n 的空间去构建线段树。

因为我们不打算考虑将线段树构建成动态的数据结构，所以使用 4n 的静态空间即可。

三：创建线段树

代码链接🔗

如果给定的数组为 arr，我们只需要开辟一个 4 * arr.length 的数组 tree 来保存线段树的节点信息即可。

建树的方式也非常简单，整体使用递归的思想，譬如我们要建立一个查询数组区间和的线段树，创建线段树代码如下：

  1. // 在 treeIndex 的位置创建区间为 [l...r] 的线段树
  2. void buildSegmentTree(int treeIndex,int l,int r){
  3.     if(l == r) {
  4.         tree[treeIndex] = arr[l]; 
  5.         return;
  6.     }
  7.     int leftTreeIndex = treeIndex * 2 + 1;
  8.     int rightTreeIndex = treeIndex * 2 + 2;
  10.     int mid = l + ((r - l) >> 1);
  11.     buildSegmentTree(leftTreeIndex,l,mid);
  12.     buildSegmentTree(rightTreeIndex,mid + 1,r);
  14.     tree[treeIndex] = tree[leftTreeIndex] + tree[rightTreeIndex];
  15. }

该方法的时间复杂度为：O(N)。

四：线段树中的区间查询

代码链接🔗

线段树的区间查询同样使用的是递归的思想，我们依旧以查询数组区间和来作为示例，代码如下：

  1. /**
  2.  * 在 treeIndex 为根的线段树中 [l...r] 的范围里，搜索区间 [queryL...queryR] 的值
  3.  *
  4.  * @param treeIndex
  5.  * @param l
  6.  * @param r
  7.  * @param queryL
  8.  * @param queryR
  9.  * @return
  10.  */
  11. int query(int treeIndex, int l, int r, int queryL, int queryR) {
  12.     if (queryL < 0 || queryL >= data.length
  13.             || queryR < 0 || queryR >= data.length
  14.             || queryL > queryR)
  15.         throw new IllegalArgumentException("Index is illegal");
  17.     if(l == queryL && r == queryR){
  18.         return tree[treeIndex];
  19.     }
  21.     int mid = l + ((r - l) >> 1);
  22.     int leftTreeIndex = treeIndex * 2 + 1;
  23.     int rightTreeIndex = treeIndex * 2 + 2;
  26.     if (queryL > mid) {// 如果查找的区间范围只在右子树中
  27.         return query(rightTreeIndex, mid + 1, r, queryL, queryR);
  28.     } else if (queryR < mid + 1) {// 如果查找的区间范围只在左子树中
  29.         return query(leftTreeIndex, l, mid, queryL, queryR);
  30.     }
  32.     int leftResult = query(leftTreeIndex, l, mid, queryL, mid);
  33.     int rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
  34.     return leftResult + rightResult;
  35. }

该方法的复杂度为：O(logN)。

五：修改线段树

代码链接🔗

修改线段树的思想也非常简单，这里就不再赘述了。

  1. public void update(int index, E e) {
  2.     if (index < 0 || index >= data.length)
  3.         throw new IllegalArgumentException("Index is illegal");
  5.     data[index] = e;
  6.     update(0, 0, data.length - 1, index, e);
  7. }
  9. /**
  10.  * 在以 treeIndex 为根节点的线段树中，更新 index 的值为 e
  11.  *
  12.  * @param treeIndex
  13.  * @param l
  14.  * @param r
  15.  * @param index
  16.  * @param e
  17.  */
  18. private void update(int treeIndex, int l, int r, int index, E e) {
  19.     if (l == r) {
  20.         // 当 l == r 说明，找到了线段树的叶子节点，该节点的值就是 data[index]，更新这个节点
  21.         tree[treeIndex] = e;
  22.         return;
  23.     }
  25.     int leftTreeIndex = getLeftChildIndex(treeIndex);
  26.     int rightTreeIndex = getRightChildIndex(treeIndex);
  28.     int mid = l + ((r - l) >> 1);
  30.     if (index <= mid)
  31.         update(leftTreeIndex, l, mid, index, e);
  32.     else
  33.         update(rightTreeIndex, mid + 1, r, index, e);
  35.     tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
  36. }

六：自下而上创建线段树

代码链接🔗

上面我们使用递归的方式构建了一棵线段树。

除了上面这种构建线段树的方法，我们还可以使用“自下而上”的思想，构建一棵线段树。

所谓的“自下而上”的含义为：先构建线段树的叶子节点。

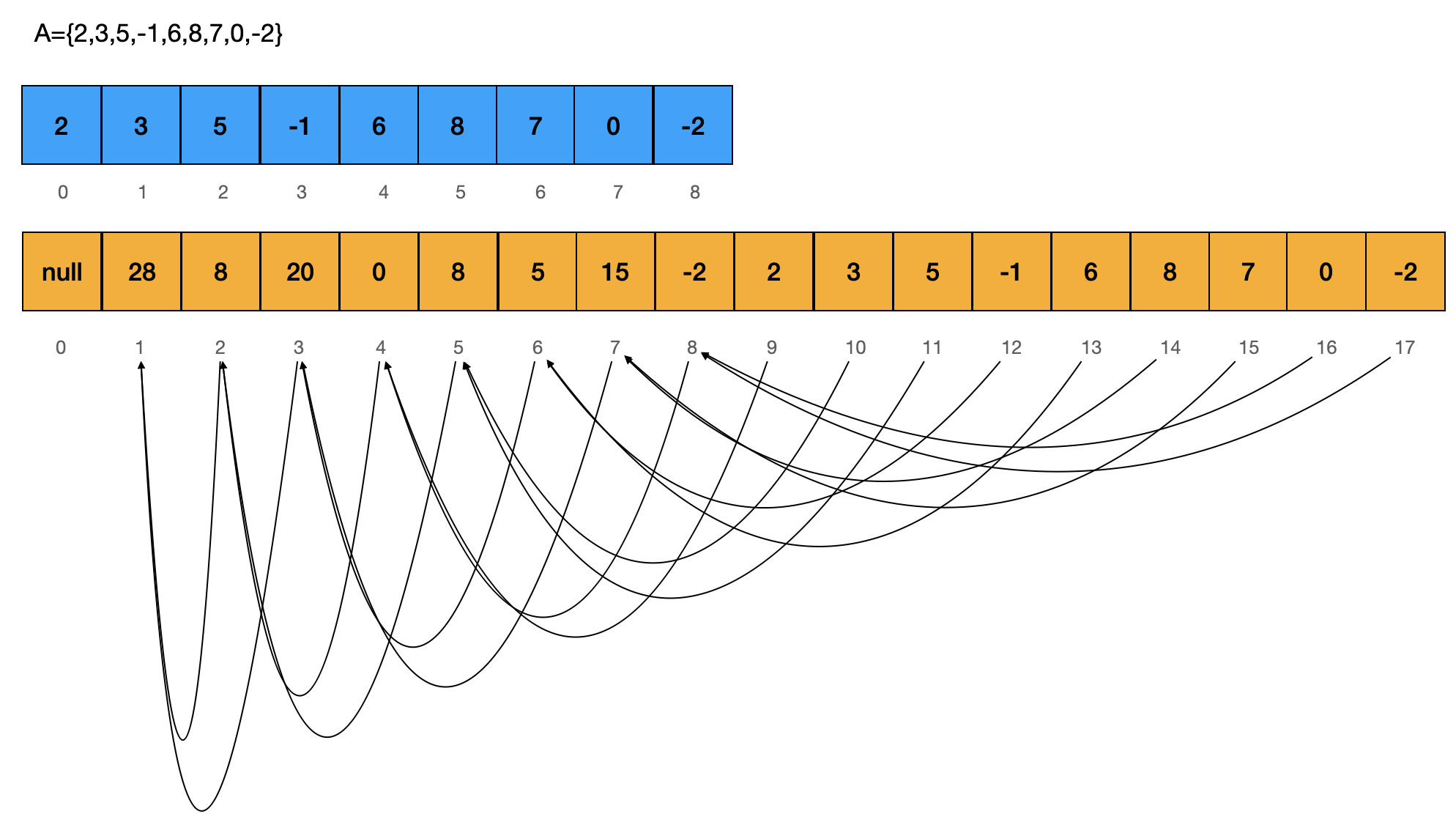
我们假定，该线段树为一棵满二叉树。这样，数组当中的所有元素恰好可以成为满二叉树的叶子节点，满二叉树节点的总数为 2n - 1 个，叶子节点为 n 个，我们将开辟 2n 的额外空间来存储整个线段树。叶子节点的索引范围为 [n,2n - 1]，这样一来，线段树的根节点的索引就是 1。

假设，我们有数组 A = [2,3,5,-1,6,8,7,0,-2]，线段树表示为区间和的信息。我们构建线段树的过程如图所示：

image.png
image.png

更新线段树

代码链接🔗

当我们更新数组中某个索引 i 处的元素时，我们也使用自下而上的方式，首先更新线段树的叶子节点，然后一路向上，直到根节点，并用其子节点的值的总和来更新每一个父节点的值。

代码如下：

  1. /**
  2.  * 更改 data 数组 index 处的元素为 val
  3.  *
  4.  * @param index
  5.  * @param val
  6.  */
  7. public void update(int index, E val) {
  8.     data[index] = val;
  9.     index += data.length;
  10.     tree[index] = val;
  11.     while (index > 1) {
  12.         int leftIndex = index;
  13.         int rightIndex = index;
  14.         if (index % 2 == 0) {
  15.             rightIndex = index + 1;
  16.         } else {
  17.             leftIndex = index - 1;
  18.         }
  19.         tree[index / 2] = merger.merge(tree[leftIndex], tree[rightIndex]);
  20.         index /= 2;
  21.     }
  22. }

该操作的时间复杂度为：O(logN)。

区域查询

代码链接🔗

依旧是使用自下而上的方式，我们对 [l,r] 这个区域范围进行查询。算法的循环不变量为：l <= r，通过子节点寻找父节点的方式是除 2，每次迭代的范围 [l,r] 都会约缩小一半，直至 logN 次后，两个边界相遇，所以该算法的时间复杂度为 O(logN)。

代码如下：

  1. /**
  2.  * 查询区间 [l...r] 的信息
  3.  *
  4.  * @param l
  5.  * @param r
  6.  * @return
  7.  */
  8. public E query(int l, int r) {
  9.     if (l < 0 || l >= data.length
  10.             || r < 0 || r >= data.length
  11.             || l > r) {
  12.         throw new IllegalArgumentException("Index is illegal");
  13.     }
  14.     l += data.length;
  15.     r += data.length;
  16.     E res = null;
  17.     while (l <= r) {
  18.         if (l % 2 == 1) {
  19.             if (res == null) {
  20.                 res = tree[l];
  21.             } else {
  22.                 res = merger.merge(res, tree[l]);
  23.             }
  24.             l++;
  25.         }
  26.         if (r % 2 == 0) {
  27.             if (res == null) {
  28.                 res = tree[r];
  29.             } else {
  30.                 res = merger.merge(res, tree[r]);
  31.             }
  32.             r--;
  33.         }
  34.         l /= 2;
  35.         r /= 2;
  36.     }
  37.     return res;
  38. }

六：线段树的更多操作

待完成…