【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：文件压缩与哈夫曼编码

假如我们有一个文件，文件当中有 A、B、C、D、E 五种字符，这五种字符出现的频率分别为 5次、4次、3次、2次、1次。

我们知道每个英文字母均占用一个字节，即 8 个比特，在不考虑该文件“其他成分”的大小时，我们可以认为原文件的大小就是15个字节，即：120 个比特。

现在，我们要将该文件进行压缩，你会怎么做？

定长编码

我们可以将 A、B、C、D、E 分别表示为 000，001，010，011，100 。原本一个字母占用 8 个比特位，现在我们仅仅使用 3 个比特位就可以表示一个字母。经过这样的转换后，压缩文件的大小为：45 个比特。

这种编码叫做固定长度编码（fixed length code），简称 FLC。

哈夫曼编码

哈夫曼编码（Huffman Coding），是一种用于无损数据压缩的熵编码，由美国计算机科学家 David Albert Huffman 在 1952 年发明。

1951年，哈夫曼在 MIT 攻读博士学位，导师 Robert Fano 给出的学期报告题目是：查找最有效的二进制编码。由于无法证明哪个已有编码是最有效的，哈夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树（哈夫曼树）编码的想法，并很快证明了这个方法是最有效的。

哈夫曼编码是一种可变长度编码（variable length code），简称 VLC。我们对文件中出现的字符的权值进行统计，出现概率高的字母使用较短的编码，反之出现概率低的字母使用较长的编码，这样使得编码之后的字符串的平均长度，期望值降低，从而达到无损压缩数据的目的。

我们接着使用上面的案例，来探究下哈夫曼编码究竟是什么？

首先，我们统计文件中每种字符的权值（出现的频率），并且将这些字符添加到一个按权值由小到大的顺序维护的优先队列中：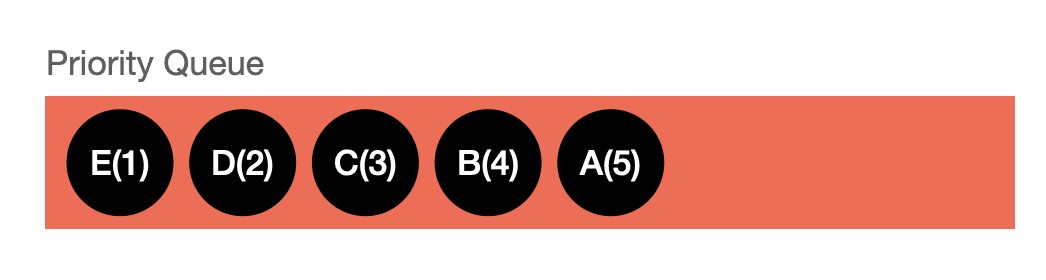
image.png
然后，我们取出权值最小的两个元素作为左右子树，将这两个元素权值的和作为根节点构造出一棵树：

image.png
将树的根节点入队：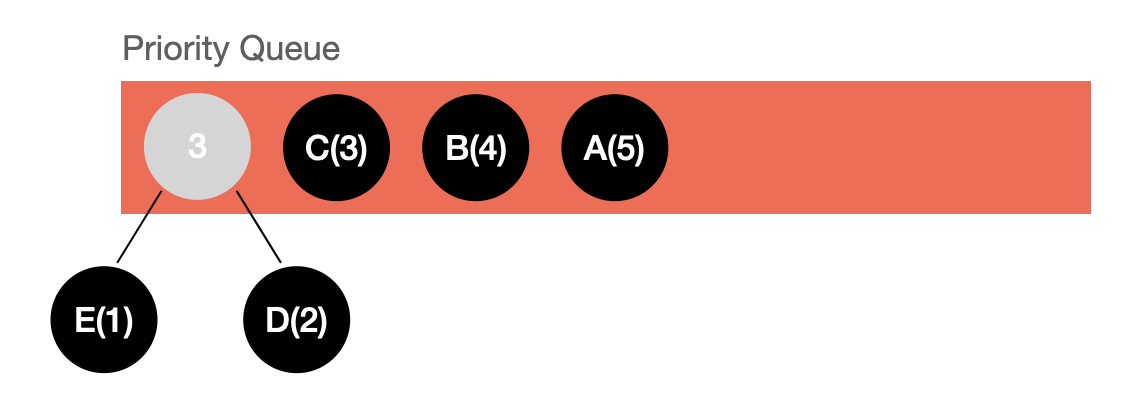
image.png
重复上述操作，直至队列为空，一棵哈夫曼树也就构建完成了。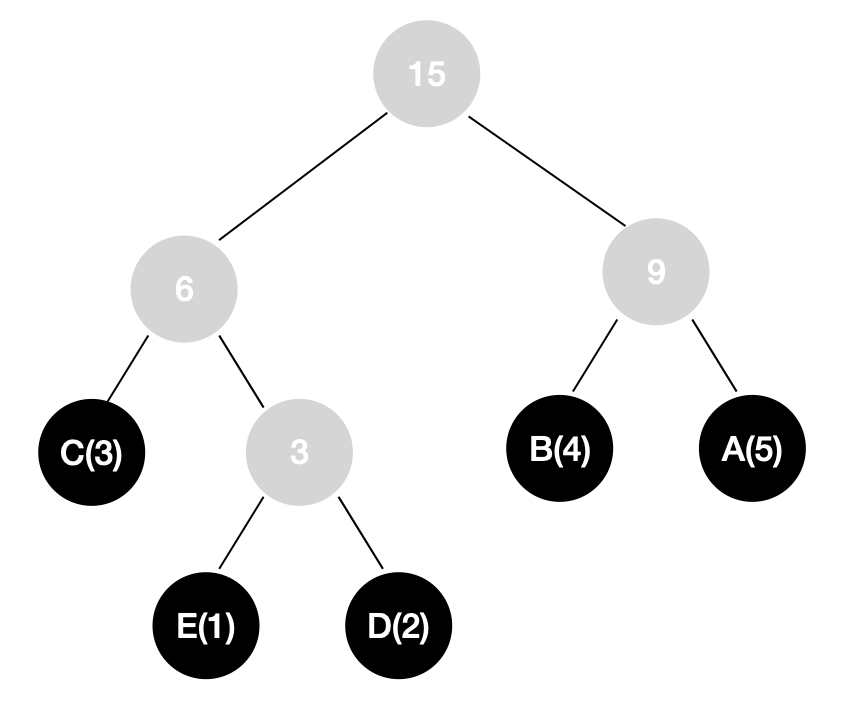
image.png

我们将这棵哈夫曼树所有的“左路径”标记为 0；所有的“右路径”标记为 1。
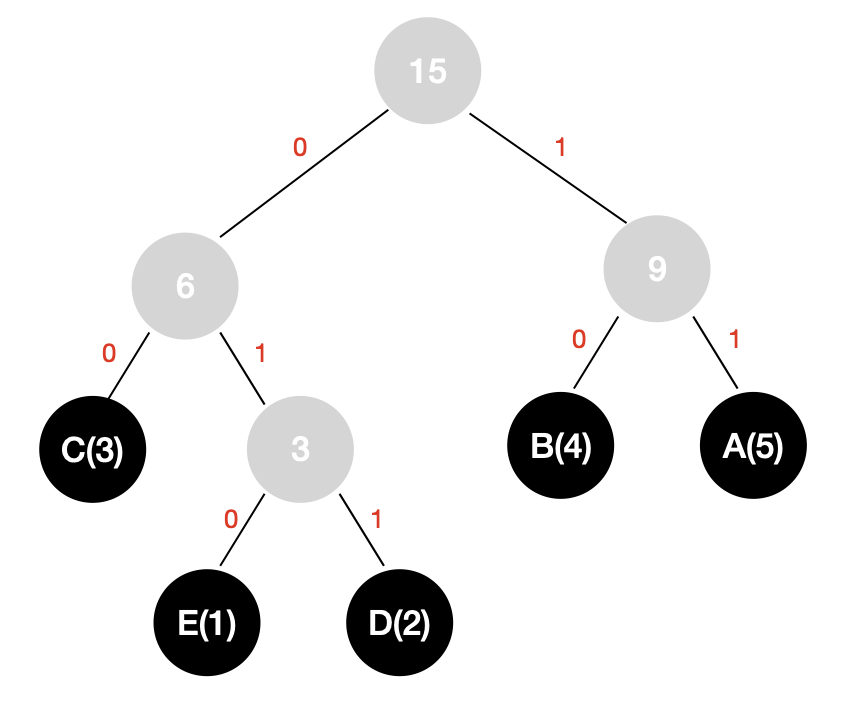
image.png
从根节点到字符的路径就是该字符对应的编码表示方式，各个字符所对应的编码依次表示为：

  • A -> 11
  • B -> 10
  • C -> 00
  • D -> 011
  • E -> 010

我们发现，原文件通过哈夫曼编码压缩后，仅占用了 33 个比特。可以看出，哈夫曼编码比定长编码方式要更加节省空间。

二：哈夫曼树

代码链接🔗

在上面我们已经简单介绍了如何生成一棵哈夫曼树，接下来，我们来了解下哈夫曼树的一些概念。

哈夫曼树的相关名词

路径

在一棵树中，一个节点到另一个节点的通路，称之为路径。

路径长度

在一条路径中，每经过一个节点，路径长度都要加一。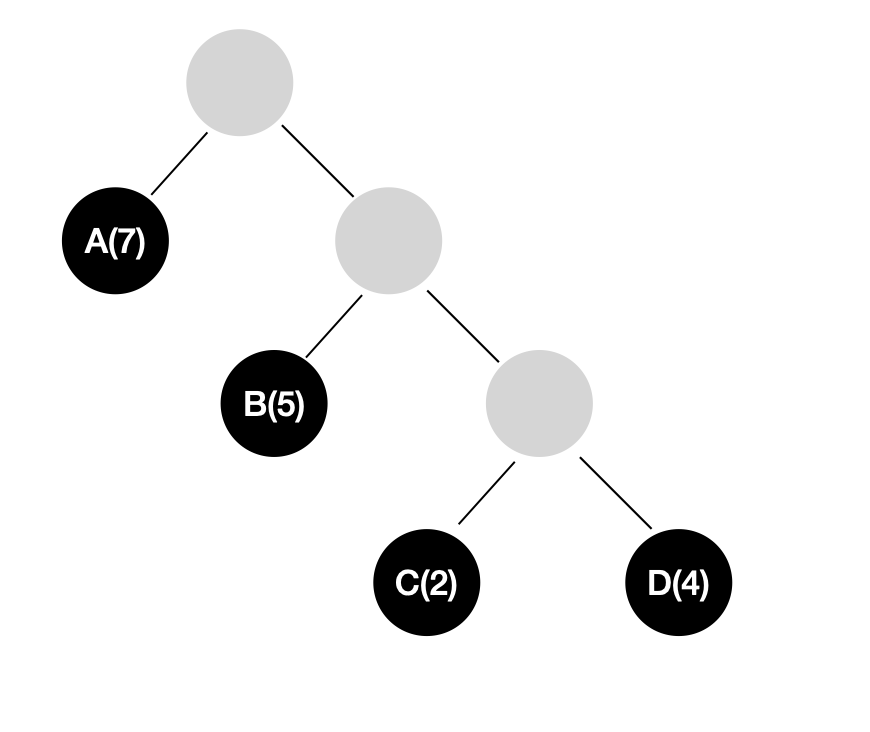
image.png
如上图所示，从根节点到节点 C 的路径长度为 3。

节点的权

节点的权重值被称为节点的权，如上图中，A、B、C、D 四个节点的权依次为 7、5、2、4。

WPL

树的带权路径长度为树中所有叶子节点的带权路径长度之和，通常记作 WPL。我们依然使用上图作为示例，该树的 WPL 为 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3 = 35

哈夫曼树的最优性证明

哈夫曼树又叫做“最优二叉树”。

这里面“最优”的含义是：当使用 n 个节点（每个节点都有自己的权值）构建一棵树时，如果构建的这棵树带权路径长度（WPL）最小，那么这棵树就是最优二叉树。

构建哈夫曼树的策略实际上是一种贪心算法（greedy algorithm）；贪心算法是一种在每一步选择中都采取当前状态下最好或最优的选择，从而希望导致结果是最好或最优的算法。

贪心算法的正确性证明比较繁琐，在贪心算法的章节中，我们会拿出来进行介绍，在这里我给出哈夫曼树的最优性证明作为拓展内容。

贪心算法的证明要满足第一步正确性证明（Greedy Choice Property）与最优子结构证明（Optimal Substructure）。

给定条件：

T(n) 为带权 w1 <= w2 <= … wn (n >= 2) 的最优树

我们的第一步是取出优先队列 n 个节点当中最小的两个节点 V(x)，V(y) 自下而上完成整个哈夫曼树的构建过程。所谓的第一步正确性证明就是，我们需要证明以 n 个节点构建的哈夫曼树中，最深的那一层一定有两个叶子节点互为兄弟节点。

假设通路最长的分支节点为 V(L_Max)，那么该分支点的子节点必然为叶子节点。假设 V(L_Max) 只有一个叶子节点 V(x)，那么 V(L_Max) 的权和 V(x) 的权相等，则可以用 V(x) 来代替分支节点 V(L_Max) 得到一棵新的树 T’(n)，则有：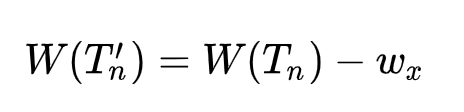
image.png

… 待完成…

在上面我们已经给出了哈夫曼树的构建过程示意图，代码也比较简单，这里就不再赘述了。

三：文件压缩与解压的实现

代码链接🔗

因为代码的篇幅比较长，我就直接给出 Demo 的链接了，请点击链接进行查看。

文件压缩与解压的流程图如下：

文件压缩流程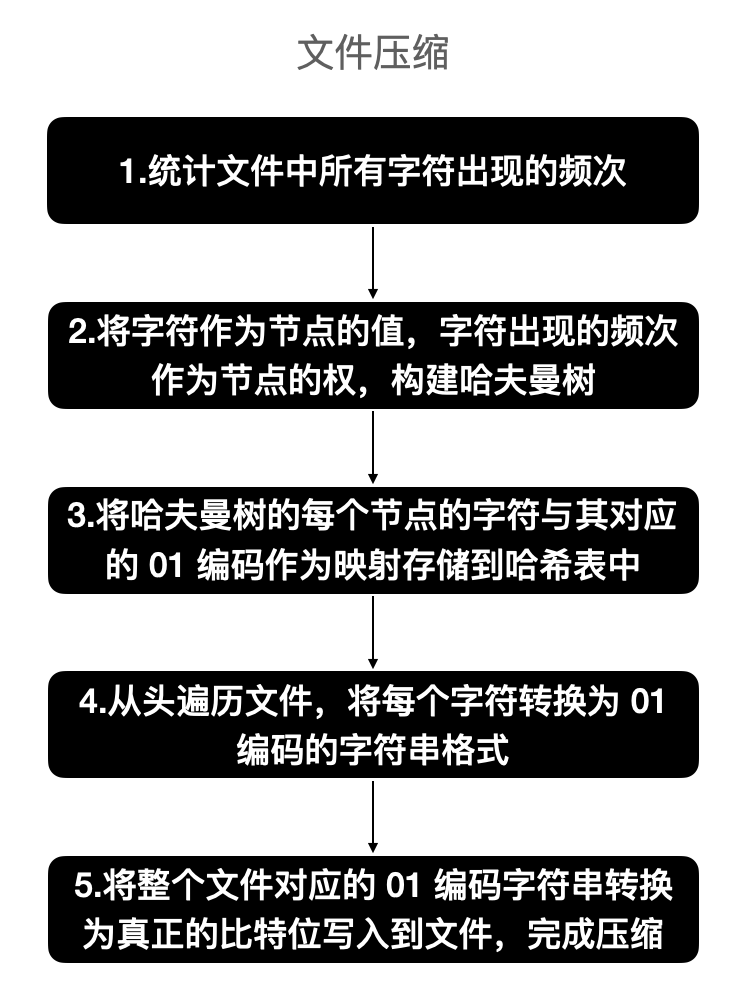
image.png

解压流程

image.png