11、前缀树

【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：什么是前缀树

前缀树（Trie）又被称为字典树或单词查找树。Trie 的典型应用是词频统计，如果文本中有 n 个条目，我们使用平衡二叉树，查询一个条目的时间复杂度为 O(logn)；如果我们使用 Trie 的话，查询每个条目的时间复杂度和数据量无关，和单词的长度相关！如果单词的长度为 w，那么时间复杂度即为 O(w)。

那么，Trie 究竟是怎样的一种数据结构呢？

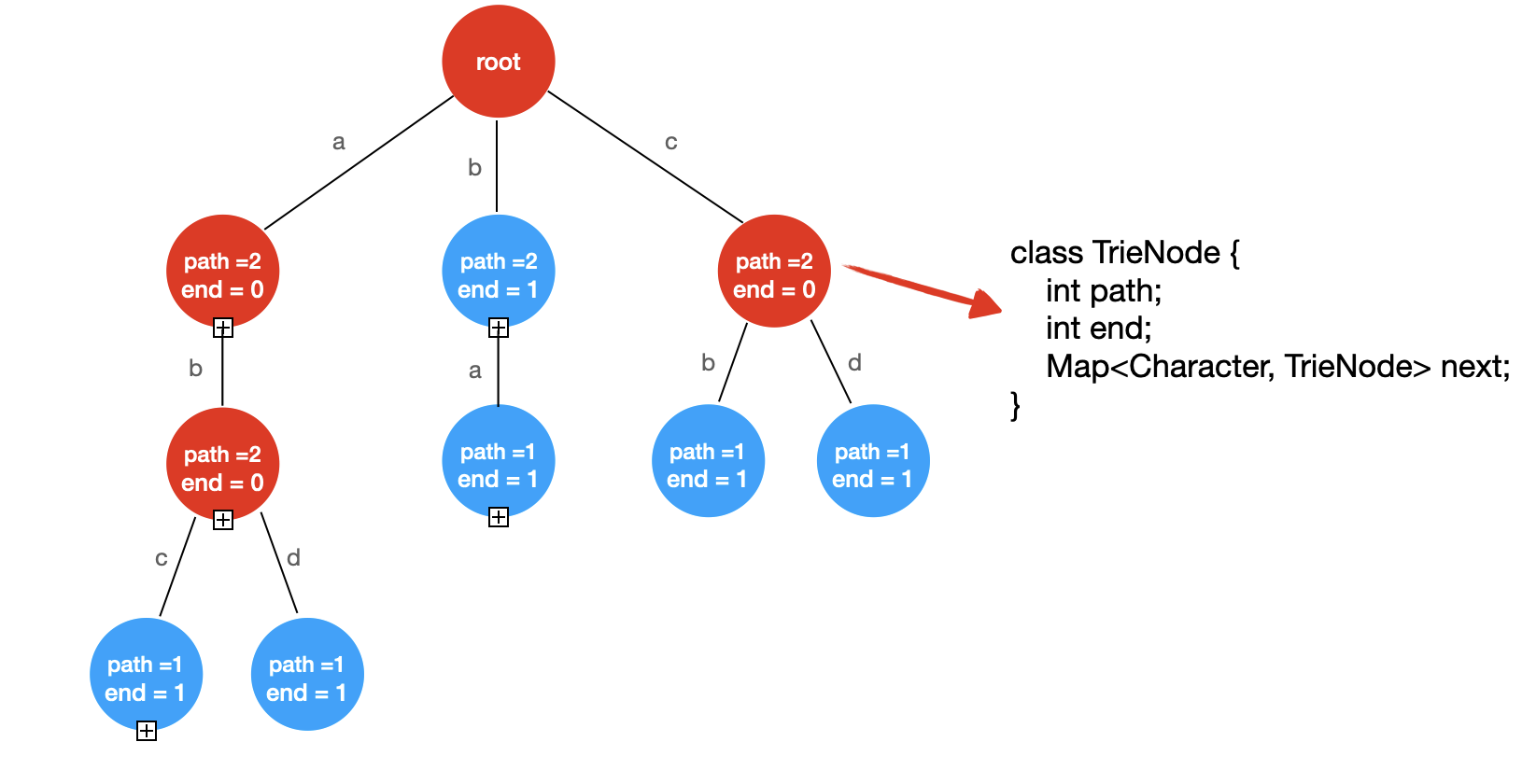
上面就是一个 Trie，我们可以看到 Trie 是一个多叉树。

在这张图中，我使用红，蓝节点表示从 root 出发直至该节点是否构成了单词，蓝色表示构成一个完整的单词，红色节点表示尚未构成单词，end 表示从 root 出发直至该节点构成了几个同样的单词；path 表示通向这个节点共有多少条路径；并且，我们使用了一个 Map 来存储该节点指向的所有的下一个节点。

上图中的 Trie 包含的所有字符串为：

{"abc","abd","b","ba","cb","cd"}

又譬如：

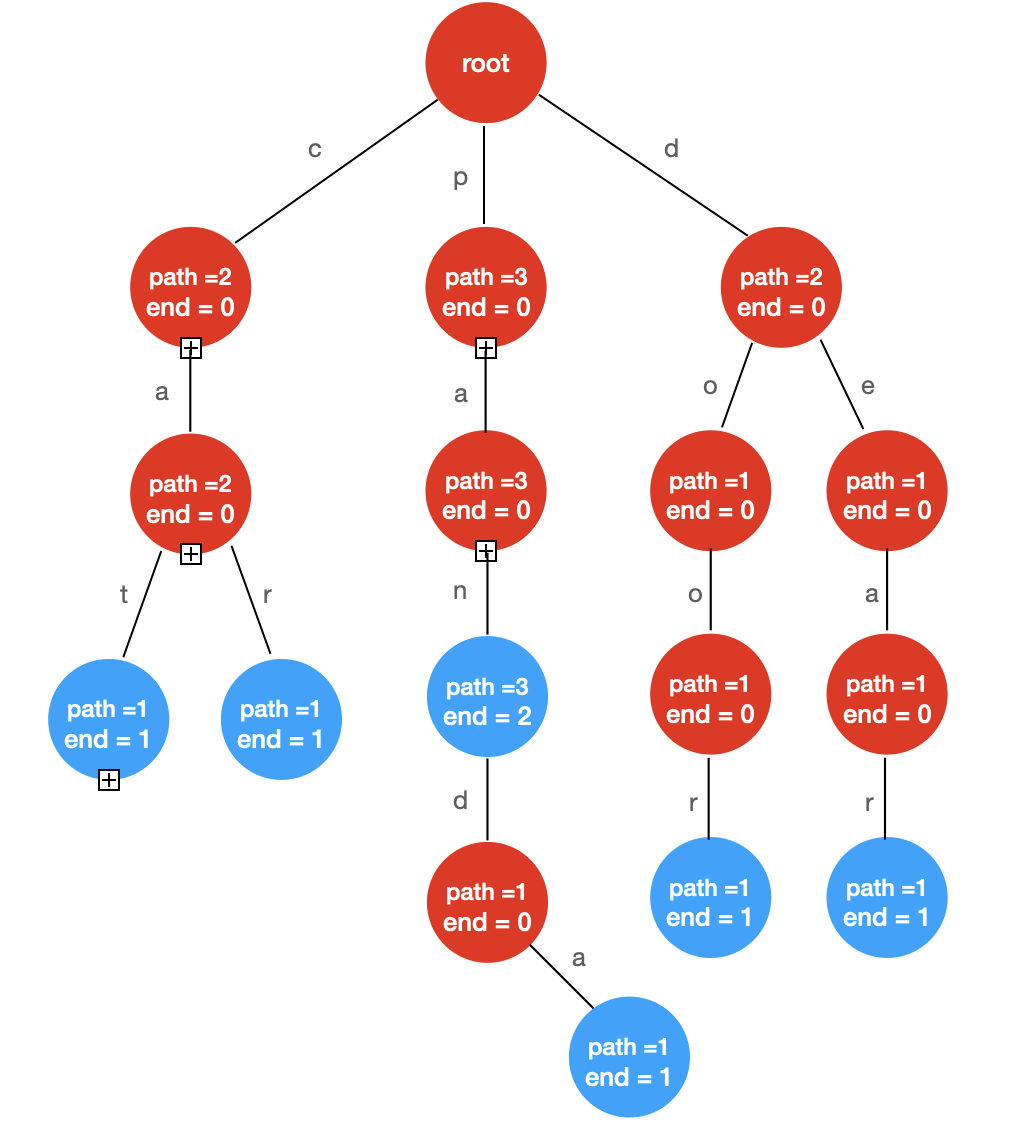
上图中的 Trie 包含的所有字符串为：

{"cat","car","pan","pan","panda","door","dear"}

要注意，我们实现的 Trie 是可以添加重复字符串的。

二：前缀树的基本方法

代码链接🔗

向 Trie 中添加，查询，删除字符串的操作非常简单，这里就不再赘述了，代码如下：

前缀树的添加操作

/**
 * 向 Trie 中添加一个单词
 *
 * @param word
 */
public void add(String word) {
    if (word == null) {
        return;
    }
    TrieNode cur = root;
    for (int i = 0; i < word.length(); i++) {
        char c = word.charAt(i);
        if (cur.next.get(c) == null) {
            cur.next.put(c, new TrieNode());
        }
        cur = cur.next.get(c);
        cur.path++;
    }
    cur.end++;
    size++;
}

前缀树的查询操作

Trie 的查询包括两种，第一种是查询 Trie 中是否包含某个单词；第二种是查询在 Trie 中有多少个以 prefix 为前缀的字符串。

contains

/**
 * 查询单词 word 是否在 Trie 中
 *
 * @param word
 * @return
 */
public boolean contains(String word) {
    if (word == null) {
        return false;
    }
    TrieNode cur = root;
    for (int i = 0; i < word.length(); i++) {
        char c = word.charAt(i);
        if (cur.next.get(c) == null || cur.next.get(c).path == 0) {
            return false;
        }
        cur = cur.next.get(c);
    }
    return cur.end > 0;
}

prefix

/**
 * 返回在 Trie 中有多少个以 prefix 为前缀的字符串
 *
 * @param prefix
 * @return
 */
public int prefix(String prefix) {
    if (prefix == null) {
        return 0;
    }
    TrieNode cur = root;
    for (int i = 0; i < prefix.length(); i++) {
        char c = prefix.charAt(i);
        if (cur.next.get(c) == null || cur.next.get(c).path == 0) {
            return 0;
        }
        cur = cur.next.get(c);
    }
    return cur.path;
}

前缀树的删除操作

/**
 * 从 Trie 中删除 word
 *
 * @param word
 */
public void remove(String word) {
    if (contains(word)) {
        TrieNode cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            cur = cur.next.get(c);
            cur.path--;
        }
        cur.end--;
        size--;
    }
}

三：Trie 和简单的模式匹配

代码链接🔗

LeetCode 211 题链接：211. 添加与搜索单词 - 数据结构设计

本题的考察点实际上就是设计 Trie 这种数据结构，不过它的要求是查找操作可以实现模式匹配。

例如，我的 Trie 中包含 “deer” 这个字符串，当我们查询的字符串为 “d..r” 时，“.” 可以代表任何字符，所以，该结果也是返回 true 的。

我们设计这个方法的方法签名为:

// TrieNode node : 遍历 Trie 的当前的节点
// String word : 查询的字符串
// int index : 遍历到字符串的哪个位置
private boolean match(TrieNode node,String word,int index)

该方法是一个递归的过程；和普通的查找有一些略微的不同，我们遍历查找的字符串，当遍历到的字符不等于 “.” 时，我们就去 Trie 对应的节点的 next 里面寻找有没有该字符，如果没有或下一个节点的 path 为 0 则返回 false，否则就继续递归。

当遍历到的字符为 “.” 时，我们就对 Trie 对应的节点的 next 里面的每一个节点进行递归，如果有一个命中，就返回 true；如果都没有命中，则返回 false。

该方法的代码如下：

/**
 * 匹配查询：
 * <p>
 * 符号 "." 可以匹配任何字符
 * 例如输入 word = d..r
 * <p>
 * 如果 Trie 中包含字符串 deer，那么 d..r 就可以匹配到 deer，结果就会返回 true
 *
 * @param word
 * @return
 */
public boolean match(String word) {
    return match(root, word, 0);
}
private boolean match(TrieNode node, String word, int index) {
    if (index == word.length()) {
        return node.end > 0;
    }
    char c = word.charAt(index);
    if (c != '.') {
        if (node.next.get(c) == null || node.next.get(c).path == 0) {
            return false;
        }
        return match(node.next.get(c), word, index + 1);
    } else {
        for (char nextChar : node.next.keySet()) {
            if (match(node.next.get(nextChar), word, index + 1)) {
                return true;
            }
        }
        return false;
    }
}