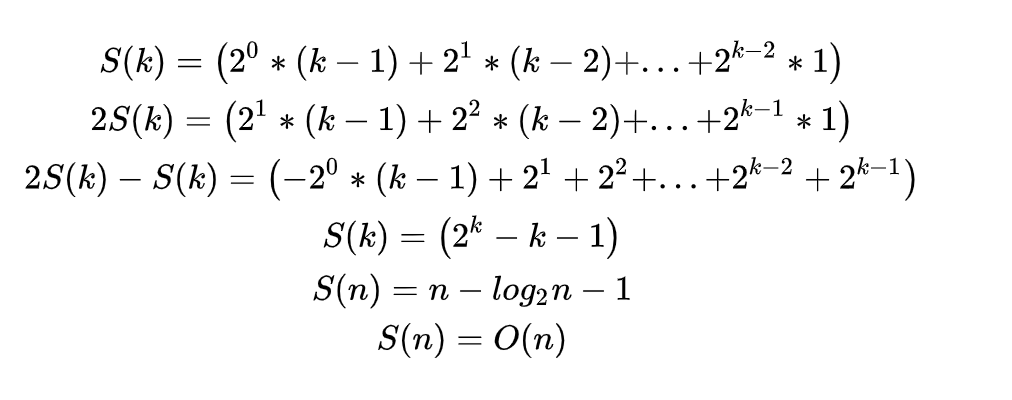7、优先队列与堆

【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：优先队列

什么是优先队列？

优先队列（Priority Queue）是一种特殊的队列。在优先队列中每个元素都有各自的优先级，优先级最高的元素最先得到服务；优先级相同的元素按照其在优先队列中的顺序得到服务。而优先队列往往使用堆来实现。

优先队列最经典的使用就是操作系统的任务调度。

我们的操作系统会同时执行多个任务，操作系统就要为这些任务分配资源，CPU 的时间片等。在分配资源时，操作系统就要动态地选择优先级最高的任务执行。

优先队列的接口

优先队列的接口在设计上和普通的队列并无差异；不过优先队列的出队操作（dequeue）要保证每次出队的元素都是队列中优先级最高的元素。

如果我们的优先队列底层使用的是线性数据结构，例如动态数组或链表，那么入队的复杂度很显然是 O(1)，而每次出队一个元素时，我们就要遍历数组或链表找到优先级最高的元素，对于遍历线性数据结构，时间复杂度则是 O(N)。这就导致，如果我们使用线性数据结构作为优先队列底层实现的话，出队就会变成一个低效的操作。

优先队列往往是用堆这种数据结构来实现的，如果使用堆作为优先队列的底层，那么入队与出队的复杂度都会是 O(logN)。

接下来，我们就来认识一下什么是堆。

二：堆

代码链接🔗

堆（Heap），一般是指二叉堆。

在了解什么是堆之前，我们首先要知道，什么是完全二叉树。

完全二叉树（Complete Binary Tree），是指对于一棵二叉树，若该二叉树的深度为 h，除了第 h 层外，其他的各个层（1～h-1）的节点数都达到了最大个数，且第 h 层所有的节点都连续地集中在最左边。

简单来说，二叉树的节点从上到下，从左至右依次排布的树就是完全二叉树。

示例：

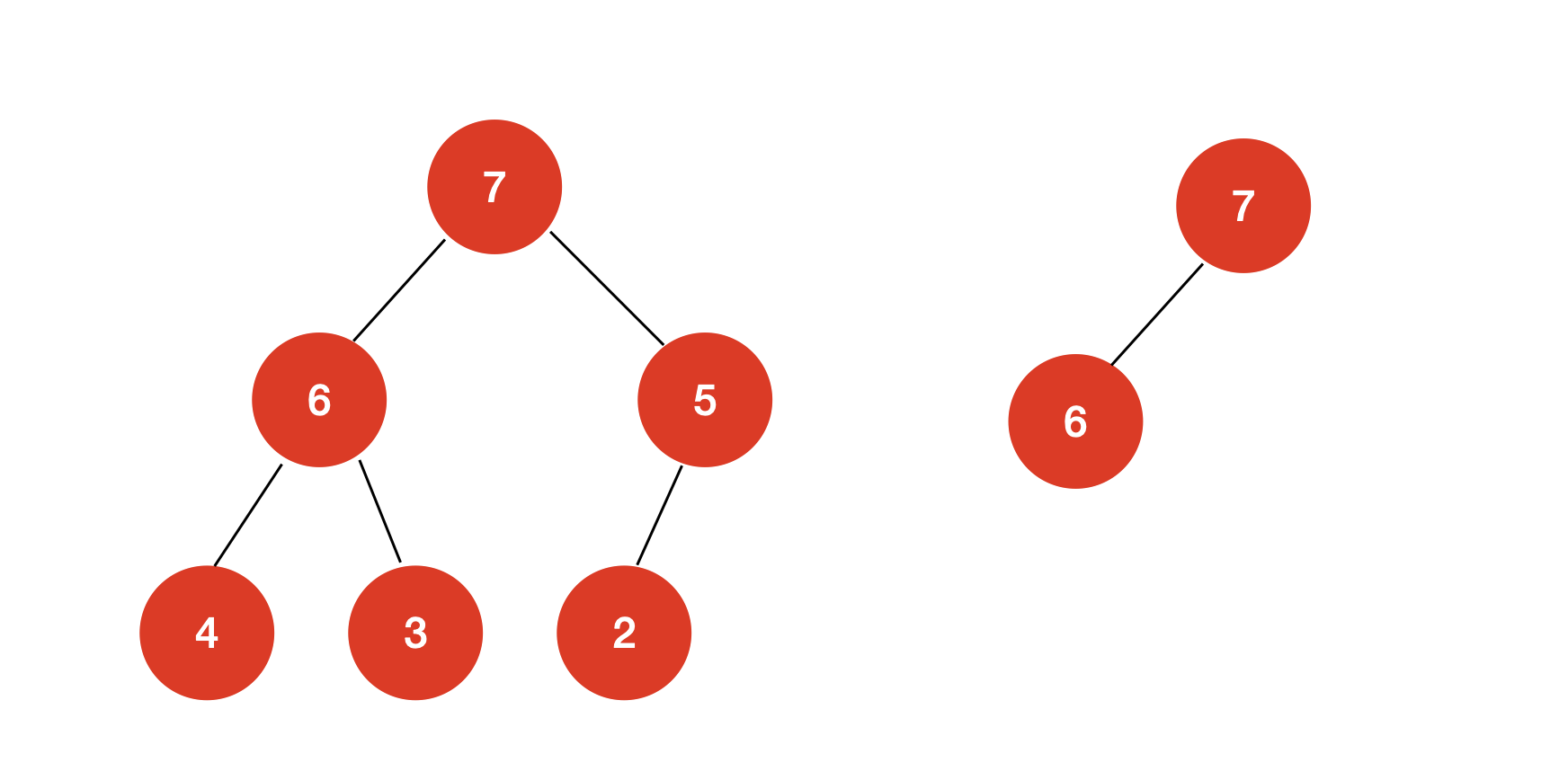
上图的两棵二叉树均为完全二叉树。

而堆就是一种完全二叉树。

大根堆与小根堆

堆分为大根堆与小根堆。

当堆中任意一个父节点的值总是大于或等于任何一个子节点的值时，我们就称之为大根堆；反之，当堆中任意一个父节点的值总是小于或等于任何一个子节点的值时，我们就称其为小根堆。

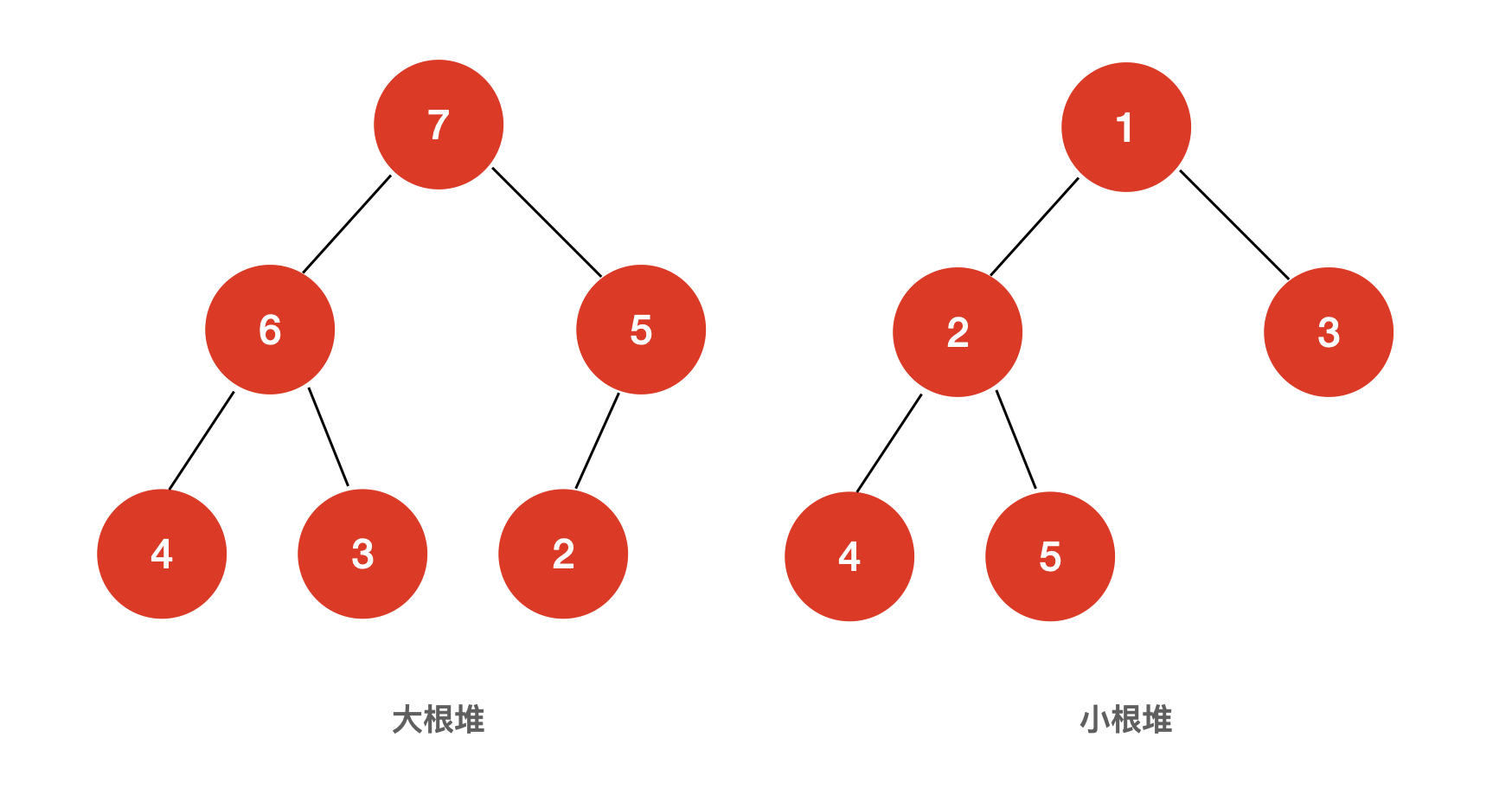
而大根堆或小根堆的任意子树仍然是大根堆或小根堆。

使用数组存储堆

虽然堆是一种树形结构，不过，我们可以使用数组来存储堆中的元素。

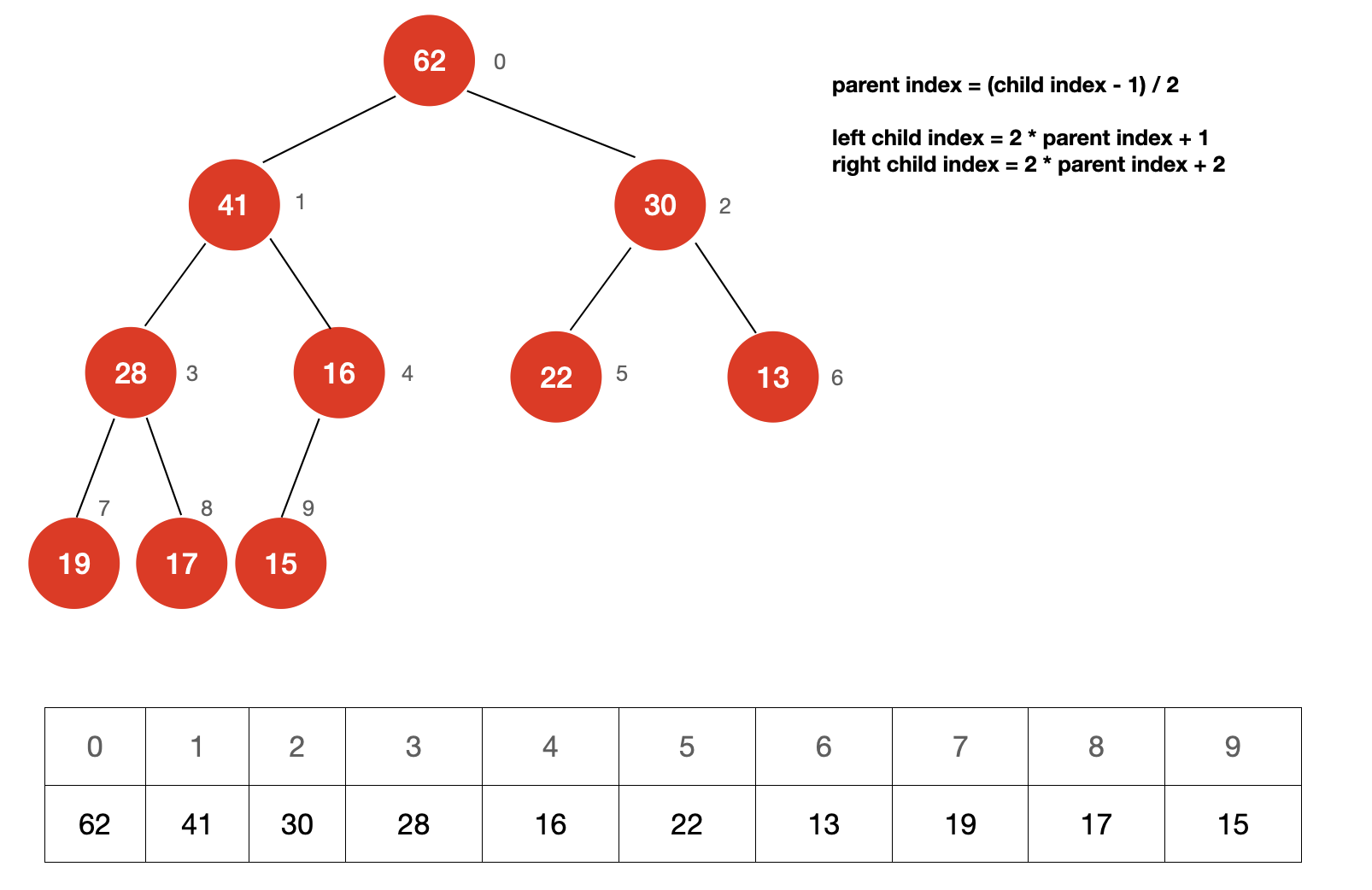
存储方式如上图所示。

三：向堆中添加元素和 Sift Up

如示例，向堆中添加一个元素 “52”

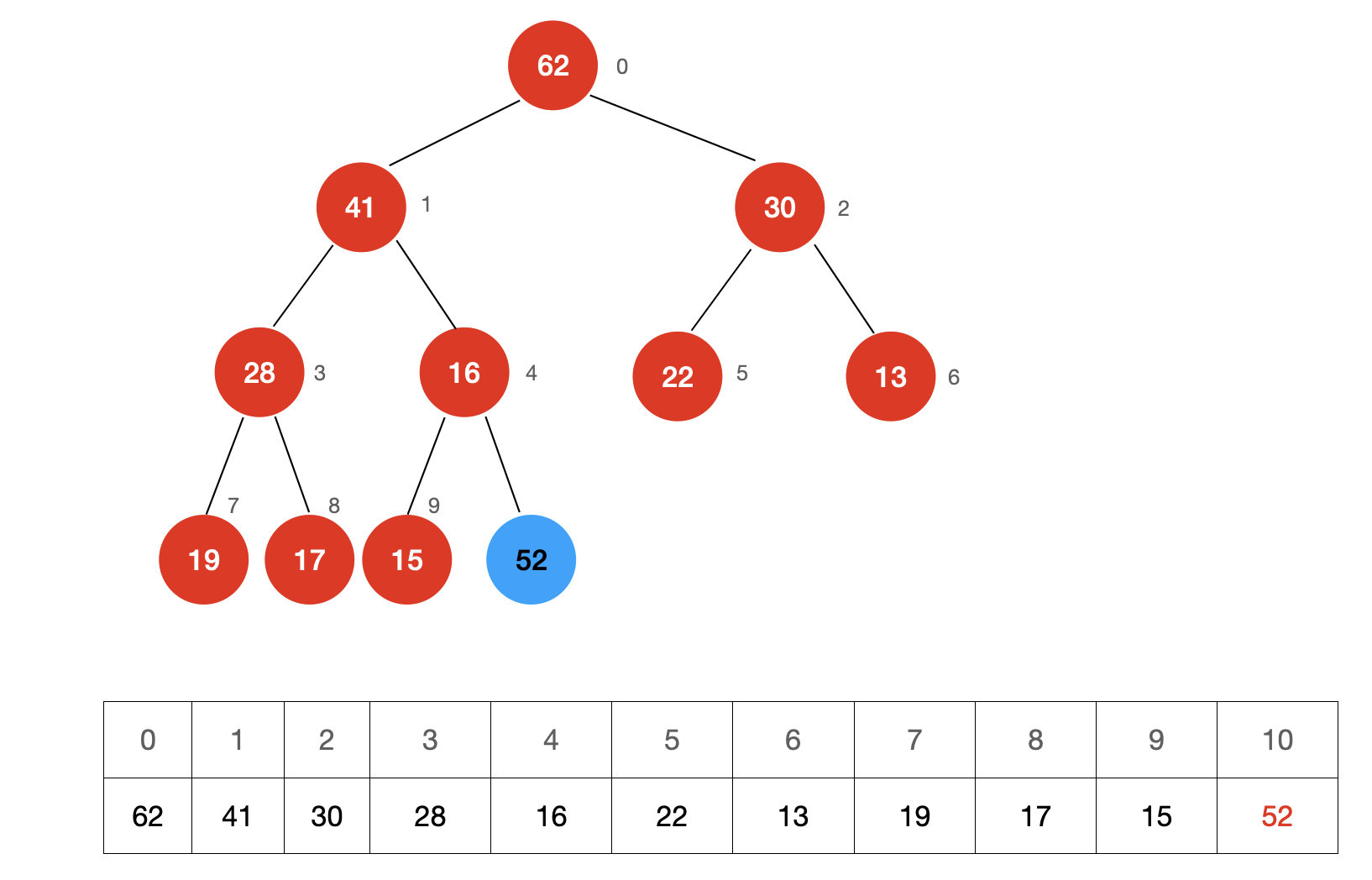
新添加的元素，为了保持大根堆的特性，需要调整节点的位置。

调整方式很简单，我们只需要让新添加的节点不断去和自己的父节点进行比较，如果新添加的节点比父节点的值要大，就交换自己和父节点的位置，直至满足小于等于父节点或自己成为了堆的根（没有父节点，成为了堆中优先级最高的节点）。

这个调整的过程叫做 Sift Up。

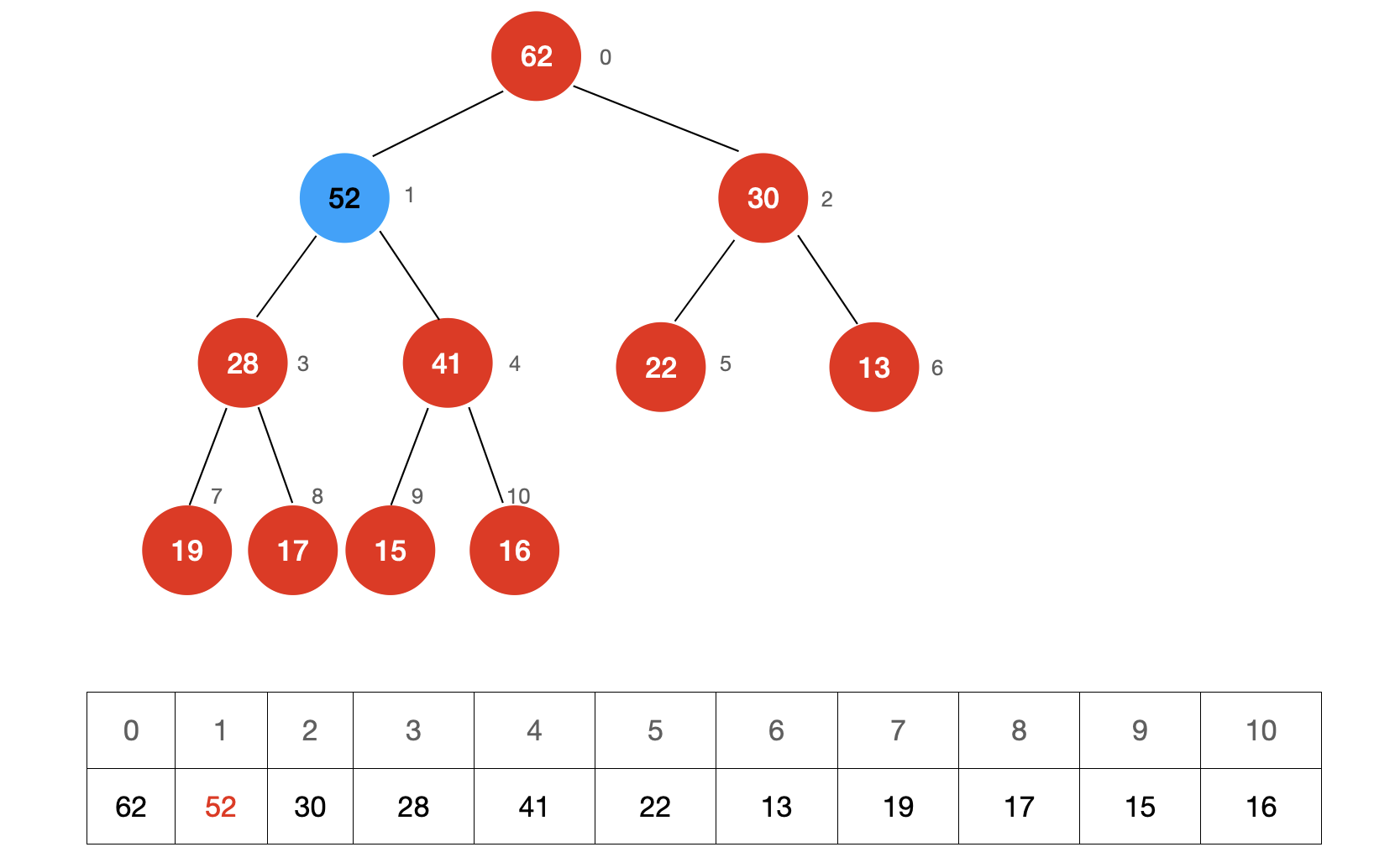
四：从堆中取出元素和 Sift Down

我们每次从堆中取出的元素就是堆的“根节点”。

从堆中取出一个元素的过程是怎么样的呢？我们依然使用上面的示例进行说明

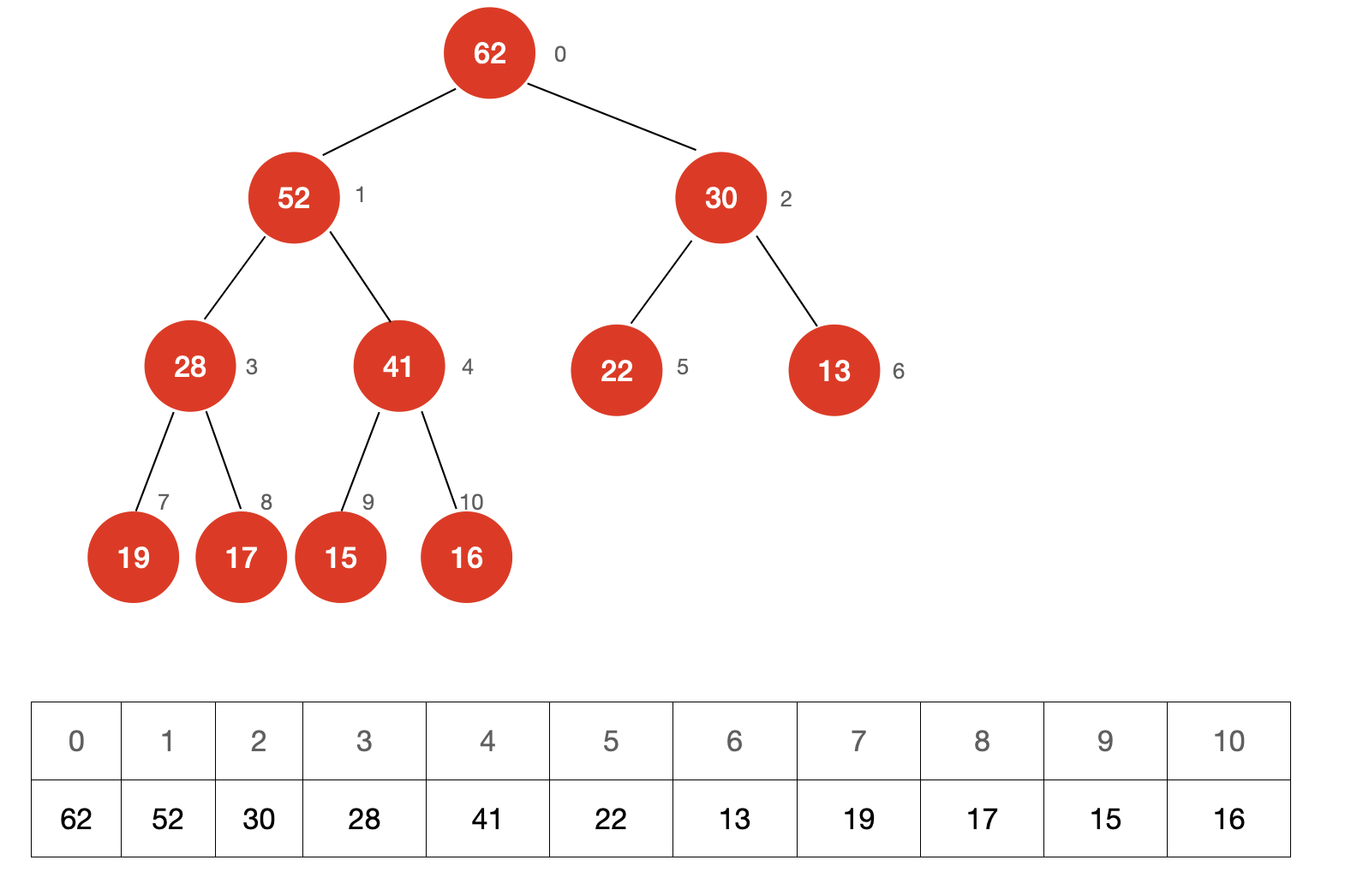
第一步：交换根节点与堆尾节点（底层数组的最后一个元素）的位置，并删除最后一个节点。

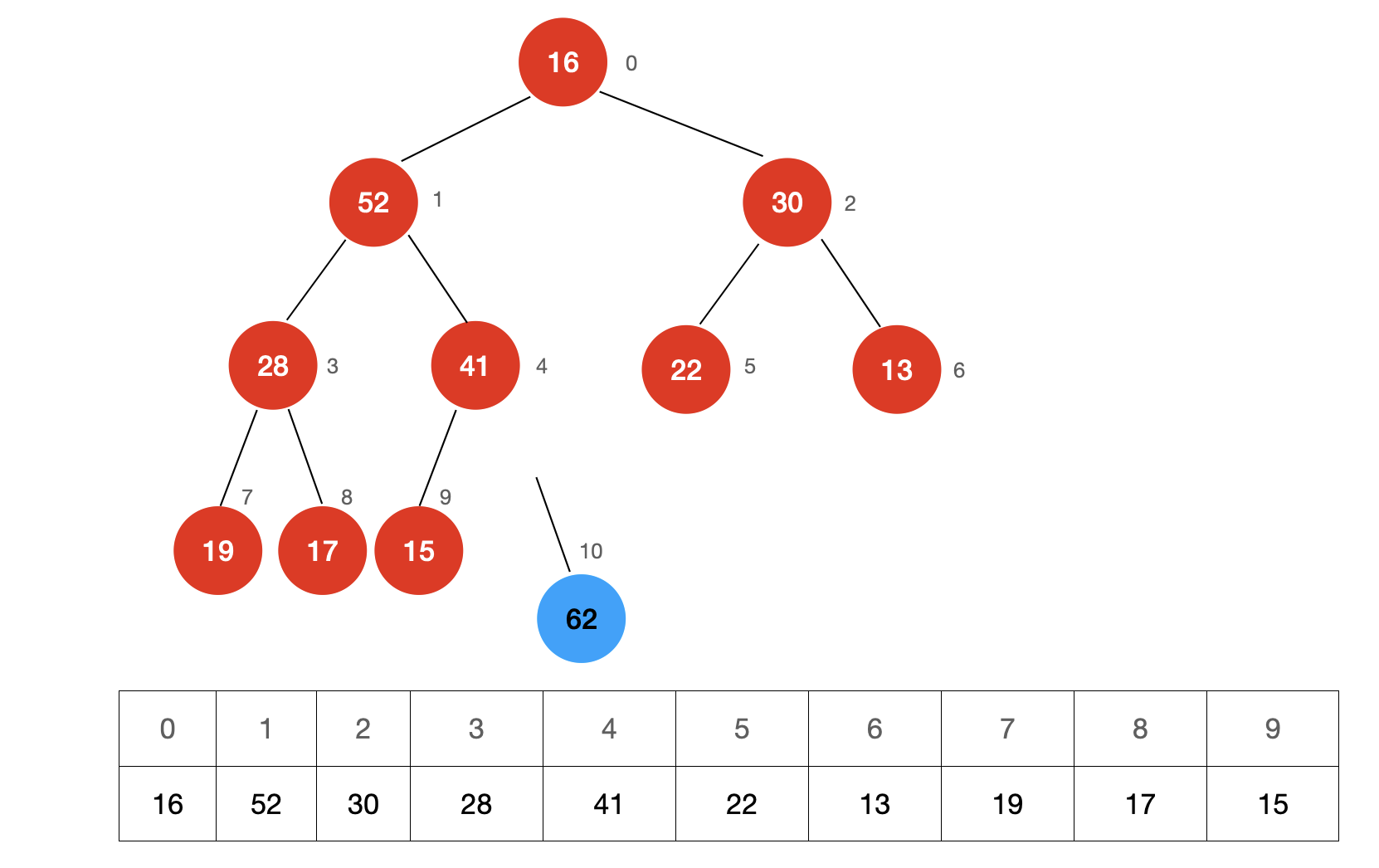
第二步：从根节点开始比较两个子节点的大小，并与较大的那一个子节点交换位置，直至满足堆的性质。

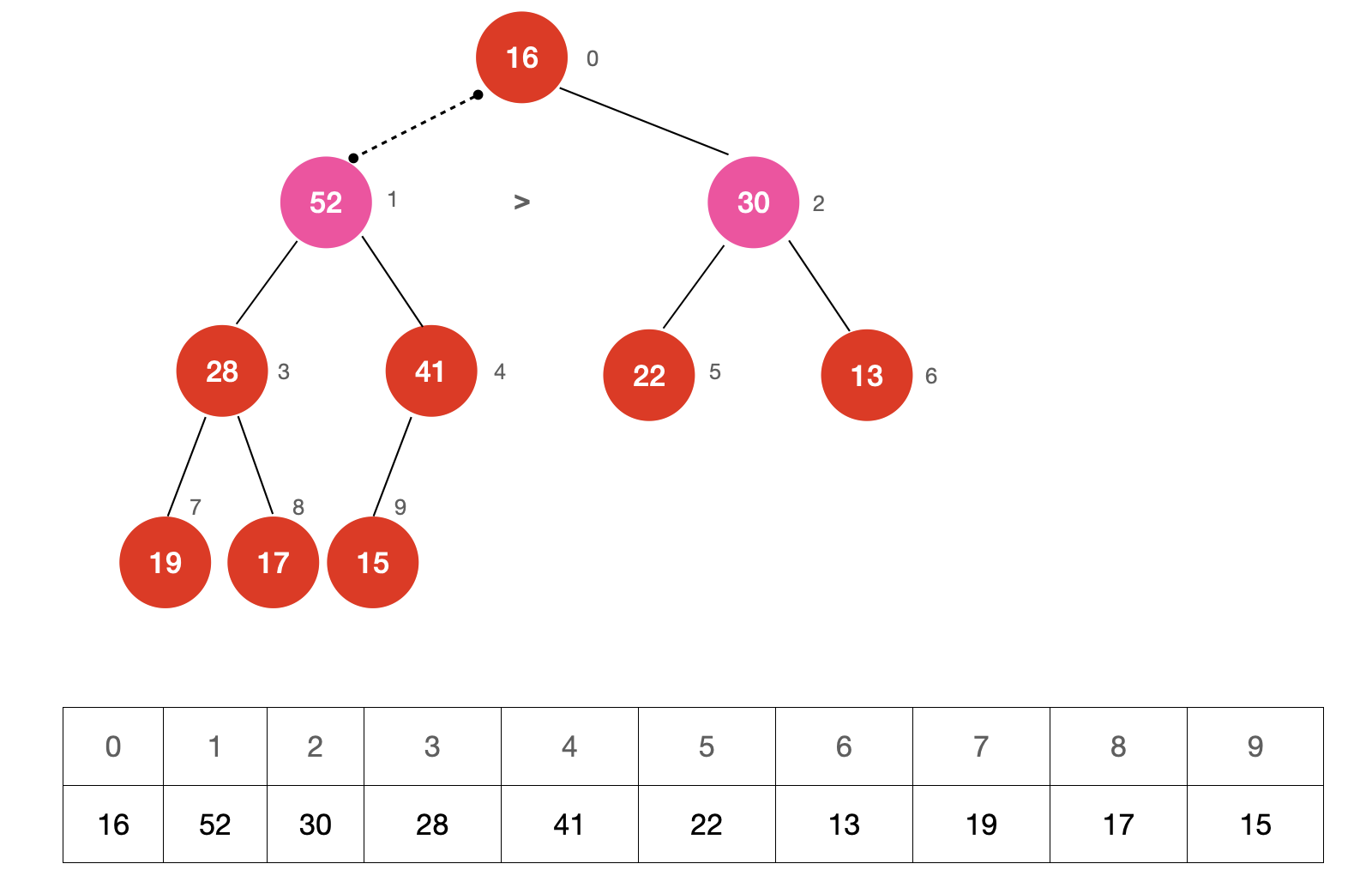
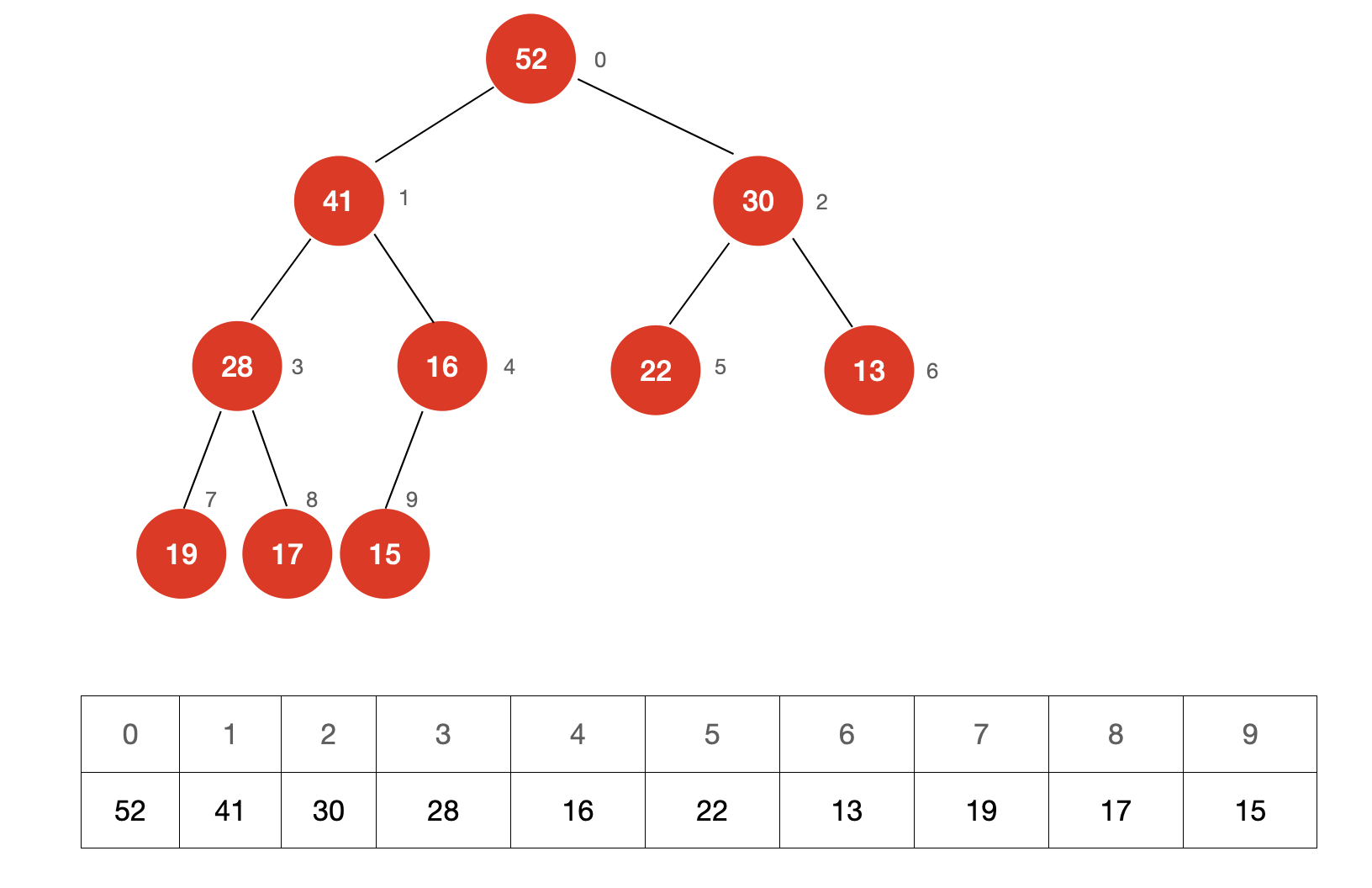
这个调整的过程叫做 Sift Down。

至此，我们其实已经完成了堆的基本操作，Sift Up 与 Sift Down 的时间复杂度均为 O(logN)，与二叉搜索树不同，堆是一棵完全二叉树，这也保证了这两种操作的复杂度是恒定的 O(logN)，不存在二叉搜索树退化成链表这种最坏的情况。

五：Heapify 和 Replace

Replace

replace 是一个方法定义，即：取出堆中的最大元素，再放入一个新的元素。

我们很自然而然地想到实现该方法可以先执行 extractMax，再执行 add。不过这样我们就做了两次 O(logN)的操作。

我们可以优化该方法，将堆顶的元素替换以后，直接执行 Sift Down，这样我们就使用了一次 O(logN)的操作完成了 repalce 方法。

Heapify

heapify 是一个方法定义，即：将任意的数组整理成一个堆。

如果是将任意的数组整理成一个堆，我们很自然而然地想到，依次将数组中的每个元素添加到堆中。比起依次向堆中添加元素，heapify 实则有更好的思路可以优化其复杂度。

例如，现有数组：

我们首先将这个数组想象成一个堆的结构

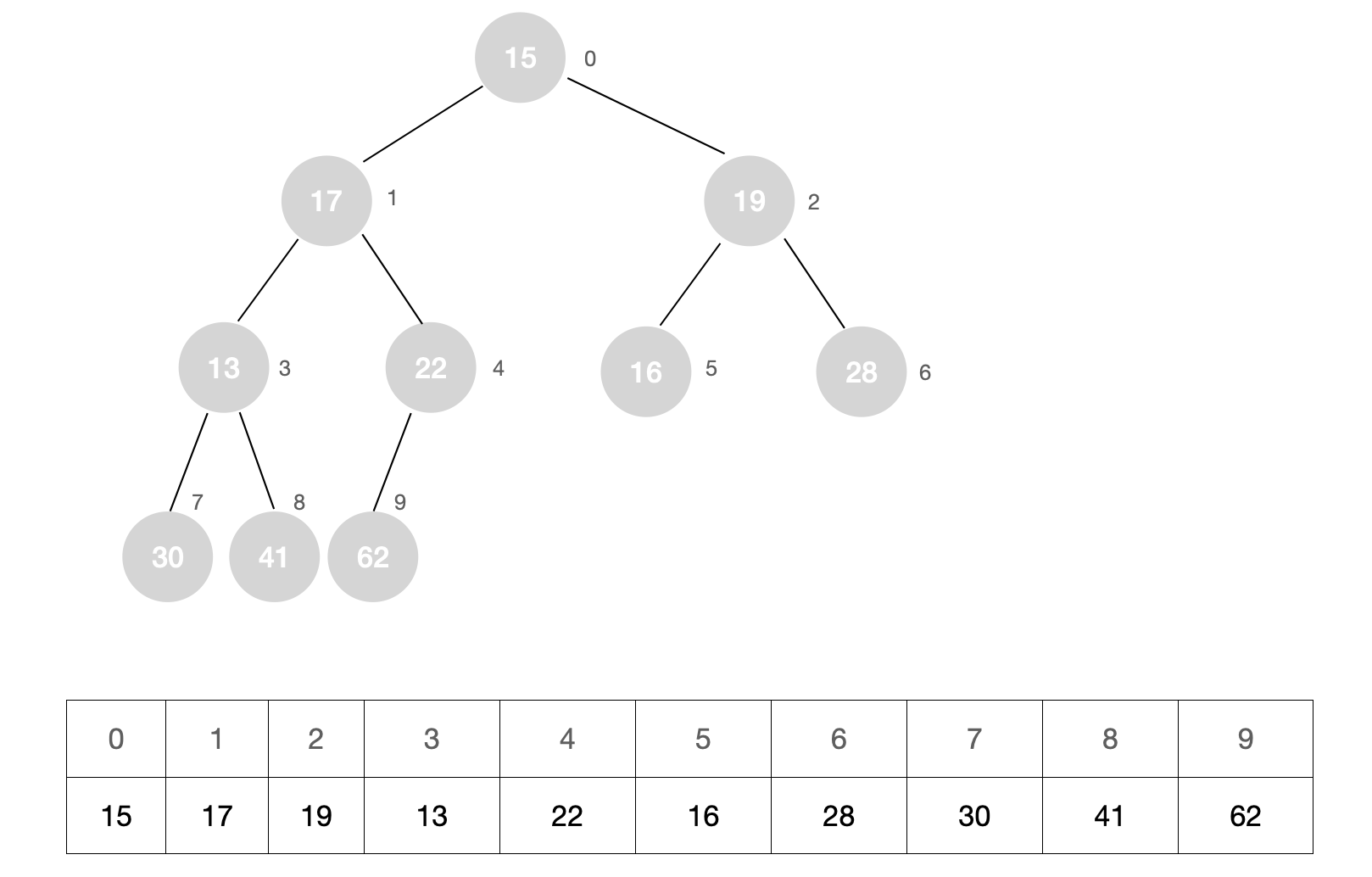
然后找到倒数第一个不是叶子节点的节点，在下图中，所有的叶子节点以蓝色标出，倒数第一个不是叶子节点的节点以红色标出。如何找到倒数第一个不是叶子节点的节点呢？其实很简单，倒数第一个节点的父节点就是倒数第一个不是叶子节点的节点。

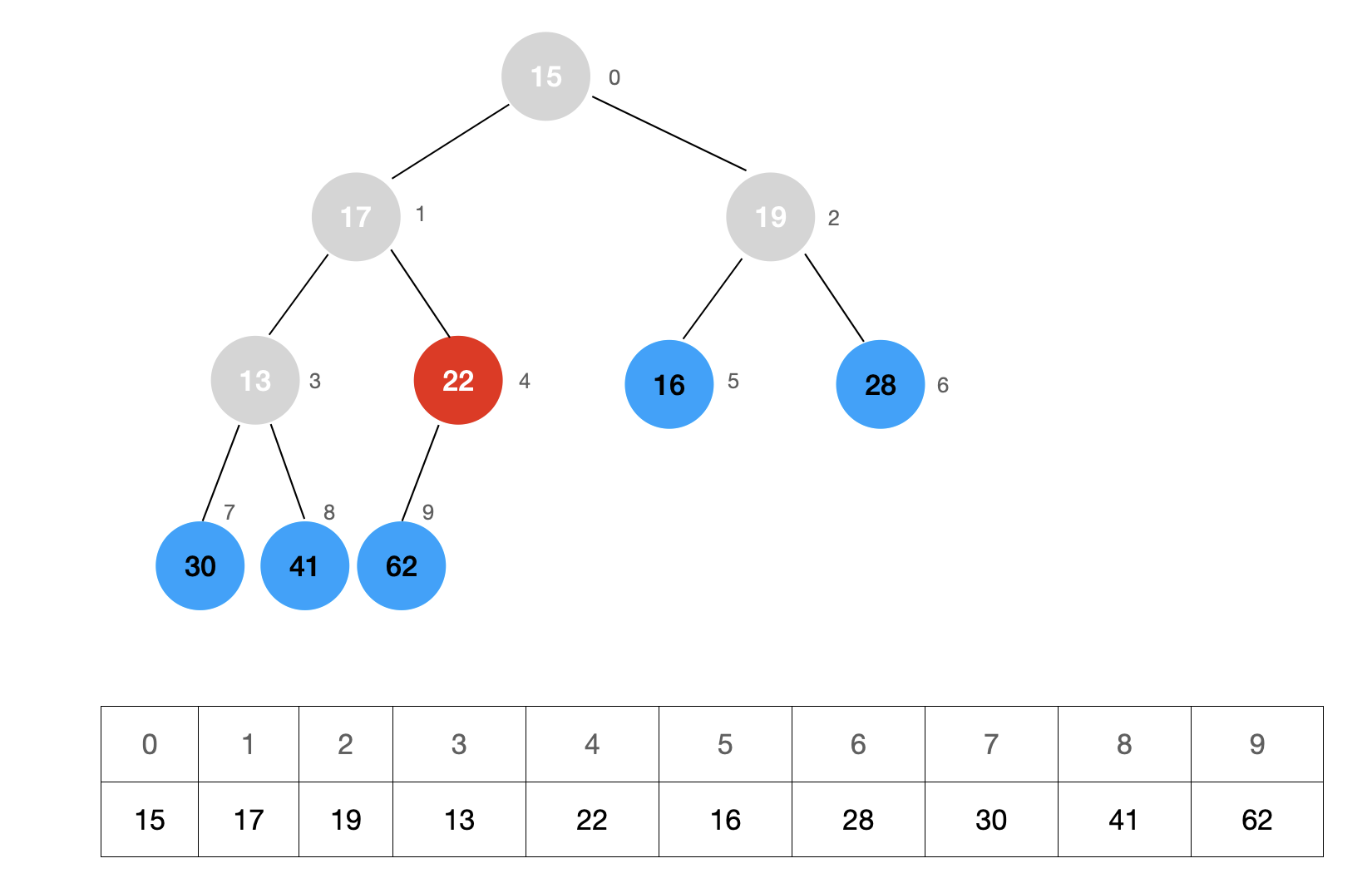
我们从倒数第一个不是叶子节点的节点开始进行 Sift Down 操作，直至整个结构符合堆的定义。

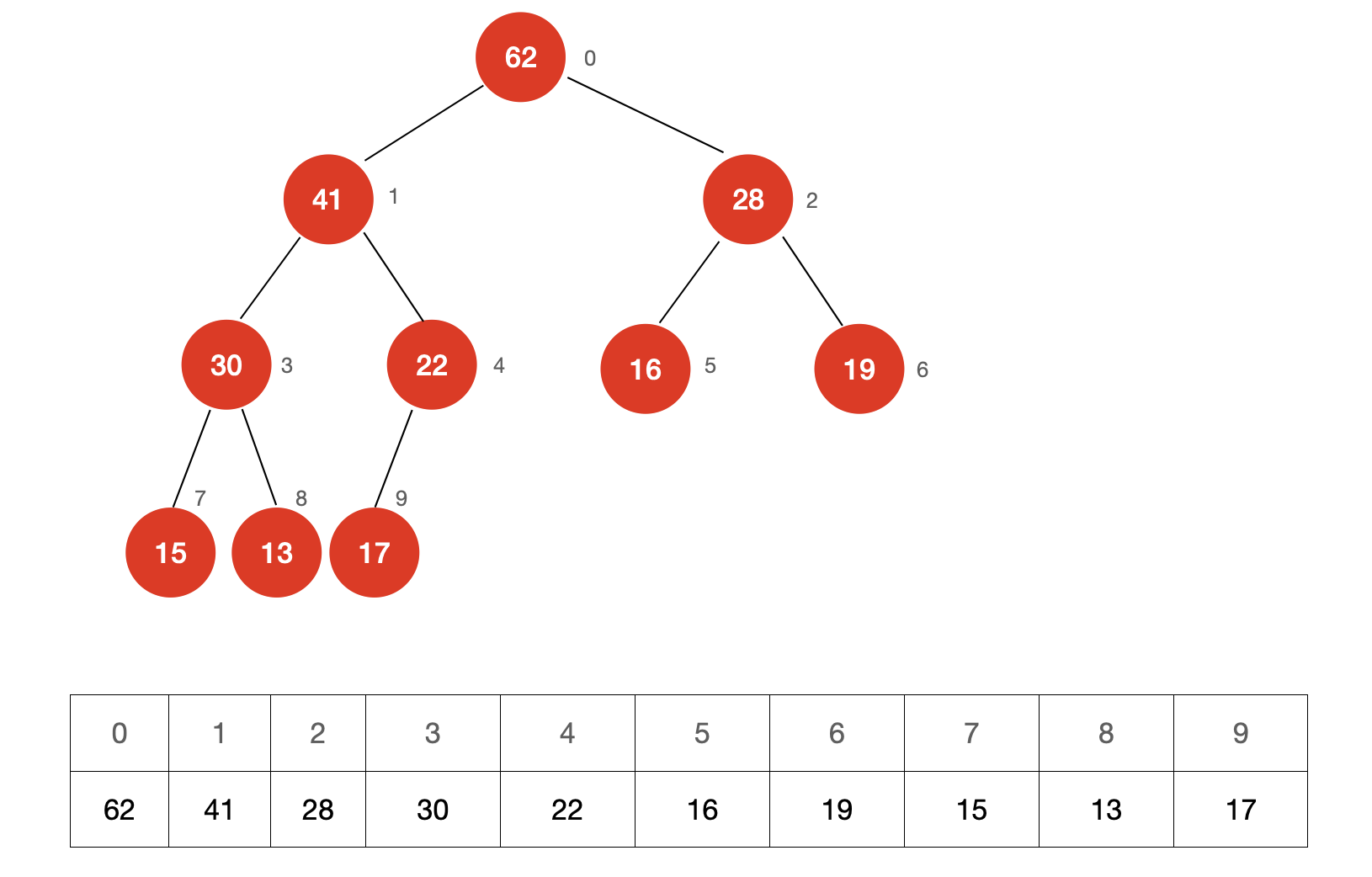
为什么这种方式要比向堆中逐个添加元素快？原因是，Sift Up 与 Sift Down 均为 O(logN) 的算法；如果使用 Sift Up 这种策略，我们就要对每一个元素都执行一次 Sift Up 操作；反之，如果使用 Sift Down 的策略，我们只需要从倒数第一个不是叶子节点的节点开始执行 Sift Down 操作即可，这相当于我们减少了一半的工作量。

如果将 n 个元素逐个插入到一个空堆中，时间复杂度很显然为 O(NlogN)；而我们的 heapify 实际上是一个 O(N) 级别的算法。

Heapify 的时间复杂度分析

我们从原数组开始

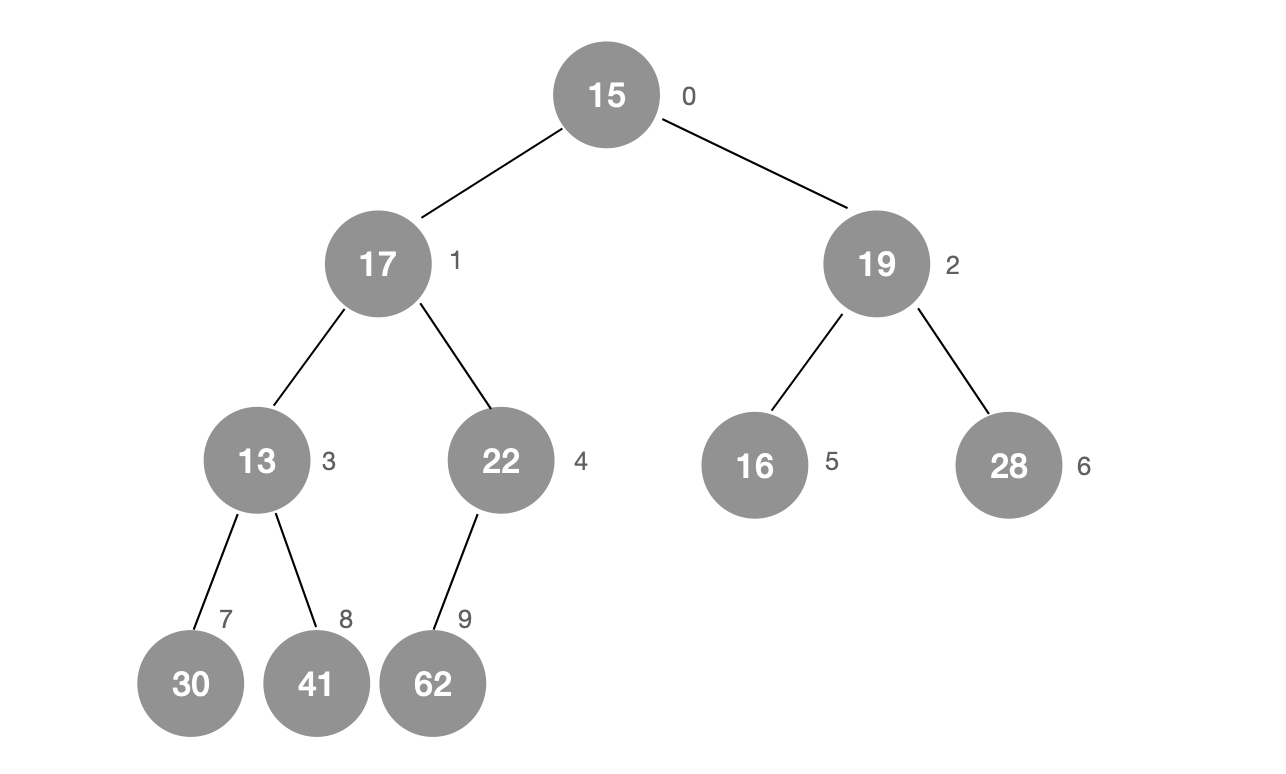
heapify 操作的时间复杂度本质上就是节点一共交换了多少次。

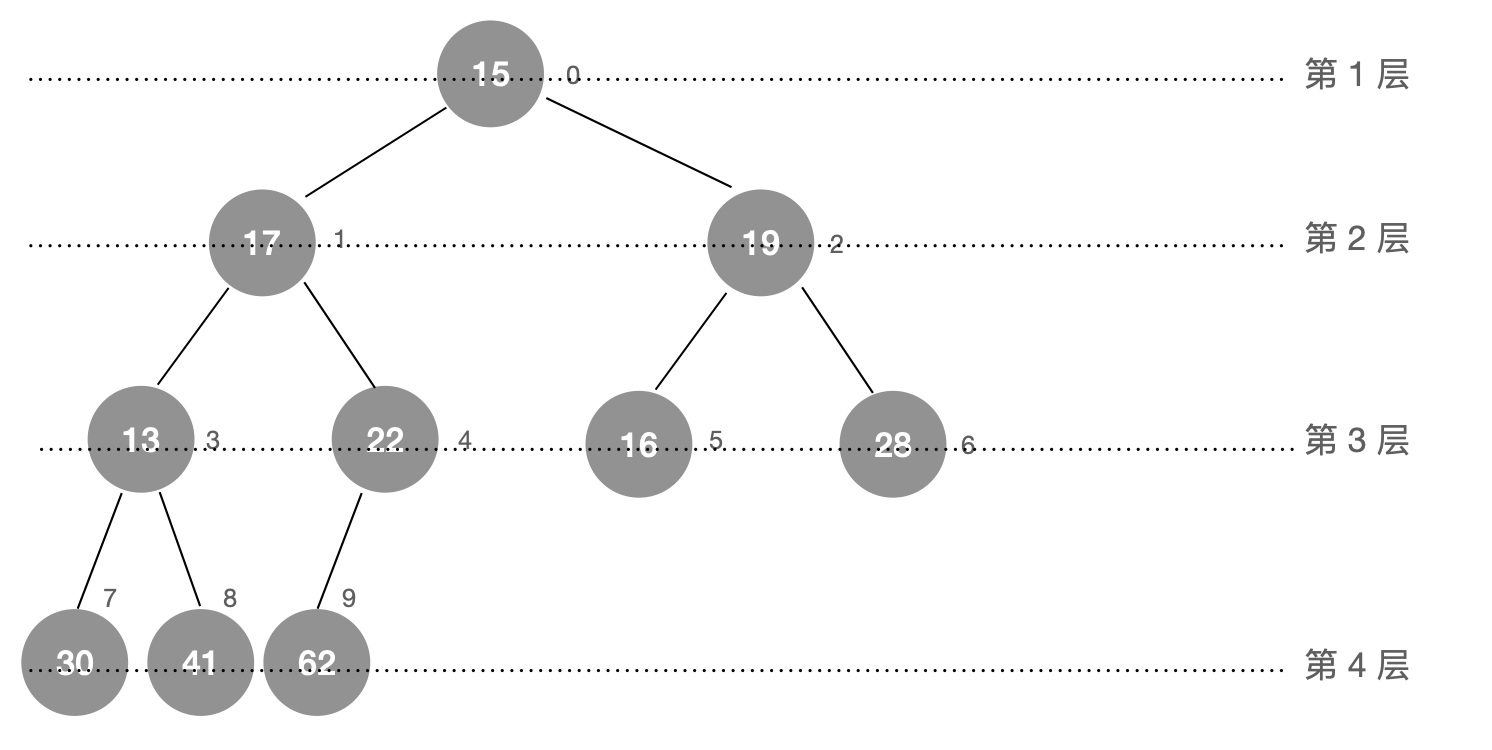
• 第一层的节点最多可以交换 3 次
• 第二层的节点最多可以交换 2 次
• 第三层的节点最多可以交换 1 次
• 第四层的节点最多可以交换 0 次

也就是说，如果堆共有 k 层，那么每一层的节点，最多的交换次数为 k - 1 次

• 第一层的节点数为 1
• 第二层的节点数为 2
• 第三层的节点数为 4
• 第四层的节点数为 3，不过当堆为满二叉树的情况下，第四层的节点数为 8

也就是说，从第一层到第 k 层，每一层的节点数为：

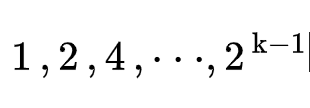
那么，总的交换次数就等于：每一层的节点数 * 每个节点最多交换的次数

设总的交换次数为 S(k)

那么，S(k) 可以表示为：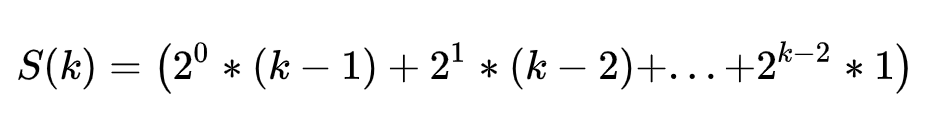

很显然，这是一个等比等差数列，求和方式为错位相减法：

所以，heapify 是一个 O(N) 级别的算法。

六：基于堆的优先队列

代码链接🔗

使用堆作为底层实现优先队列。

七：经典问题 Top K 问题

347. 前 K 个高频元素

本题就是一道经典的 Top K 问题，使用 Java 自带的优先级队列即可解决，代码比较简单，在这里就不再赘述了。

代码：

class Solution {
    private class Freq {
        int e;
        int freq;
        public Freq(int e, int freq) {
            this.e = e;
            this.freq = freq;
        }
    }
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            if (map.containsKey(num)) {
                map.put(num, map.get(num) + 1);
            } else {
                map.put(num, 1);
            }
        }
        java.util.PriorityQueue<Freq> priorityQueue = new java.util.PriorityQueue<>((o1, o2) -> {
            if (o1.freq > o2.freq) {
                return 1;
            } else if (o1.freq < o2.freq) {
                return -1;
            } else {
                return 0;
            }
        });
        for (int key : map.keySet()) {
            if (priorityQueue.size() < k) {
                priorityQueue.offer(new Freq(key, map.get(key)));
            } else if (map.get(key) > priorityQueue.peek().freq) {
                priorityQueue.remove();
                priorityQueue.offer(new Freq(key, map.get(key)));
            }
        }
        int[] res = new int[priorityQueue.size()];
        for (int i = 0; i < res.length; i++) {
            res[i] = priorityQueue.remove().e;
        }
        return res;
    }
}