2、栈 - 《数据结构》

一：栈与栈的应用
- 什么是栈？
- 无处不在的栈——栈的应用
二：栈的基本实现
三：括号匹配问题

【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：栈与栈的应用

什么是栈？

栈（Stack）是一种运算受限的线性数据结构，所谓的运算受限指的是：栈这种数据结构仅允许在一端添加元素，删除元素，这一端被称作栈顶，而相对的另一端被称为栈底。

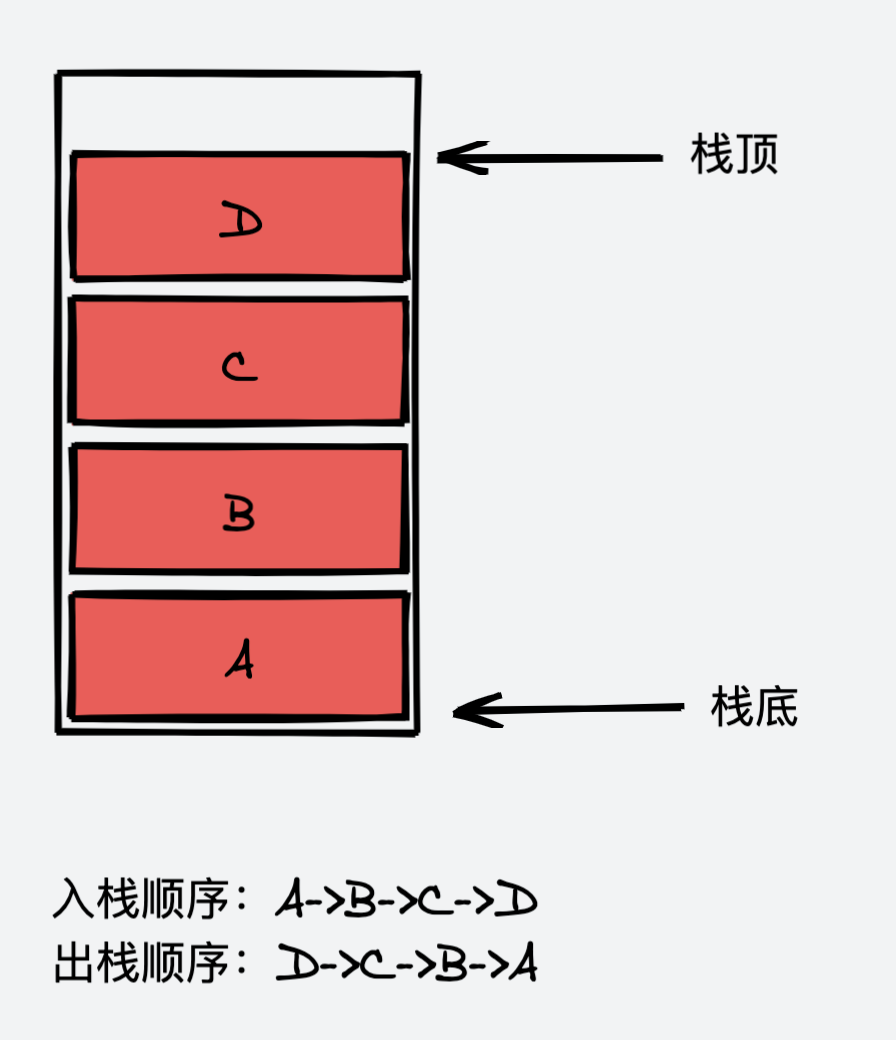
元素 A 最先进栈，最后出栈，元素 D 最后进栈，最先出栈。

所以，栈具有这种后进先出（LIFO-> Last In First Out）的特性。

无处不在的栈——栈的应用

在我们日常生活所能接触到的各种软件中，只要你留意，就会发现栈的身影。

1. Undo（撤销操作）

我们在文档编辑器中输入文字，当发现输入错误，想要撤销到前一步，这个操作就是Undo（撤销）。

撤销实际上就是通过栈这种数据结构来设计实现的。

2. 浏览器的前进与后退

浏览器页面的前进与后退到上一个页面的功能也是通过栈来实现的。

3. C语言的 printf() 函数

我们来看一个 C 程序：

#include<stdio.h>
int main(void){
    int i=1;
    printf("%d%d%d",i,i++,i++);
    return 0;
}

你知道这个程序运行的结果是什么嘛？

如果你只是知道 i++ 与 ++i 的区别，而不了解 C 语言中 printf() 函数的底层实现原理，肯定是说不出正确答案的。

该程序的运行结果为：

因为 printf 函数的底层实现就是栈。

printf 函数会将传入参数以从右到左的顺序入栈，并将结果保存后出栈。

push(i++)；保存结果为 1
push(i++)；保存结果为 2
push(i)；保存结果为 3

出栈顺序为：3，2，1

4. 程序调用系统栈

我们来看一个 Java 程序：

package com.github.test;
public class Test {
    public static void main(String[] args) {
        A();
    }
    public static void A() {
        B();
    }
    public static void B() {
        C();
    }
    public static void C() {
        System.out.println("In method C");
    }
}

程序的 main 方法调用了 A 方法，A 方法中调用了 B 方法，B 方法中调用了 C 方法。

大家是否有想过，在这些方法的调用中，我们的编译器是如何记录程序运行到哪一步，并且应该带着返回值回到哪里的呢？

答案就是：大名鼎鼎的方法栈。

方法栈会以栈桢为单位进行压栈与出栈操作，每一个方法从调用开始到执行完成，都对应着一个栈桢在方法栈从入栈到出栈的过程。

栈桢存储了方法的局部变量表，操作数栈，方法返回地址等信息，因为我们的重点是数据结构，关于栈桢的一些详细的说明就不在这里展开了，我们来重点看一下方法栈发生了什么：

从 main 方法开始，方法逐个调用直至进入到 C 方法，方法栈会一直压栈，只有位于栈顶的栈桢才是有效的，称为当前栈桢，与这个栈桢相关联的方法称为当前方法。

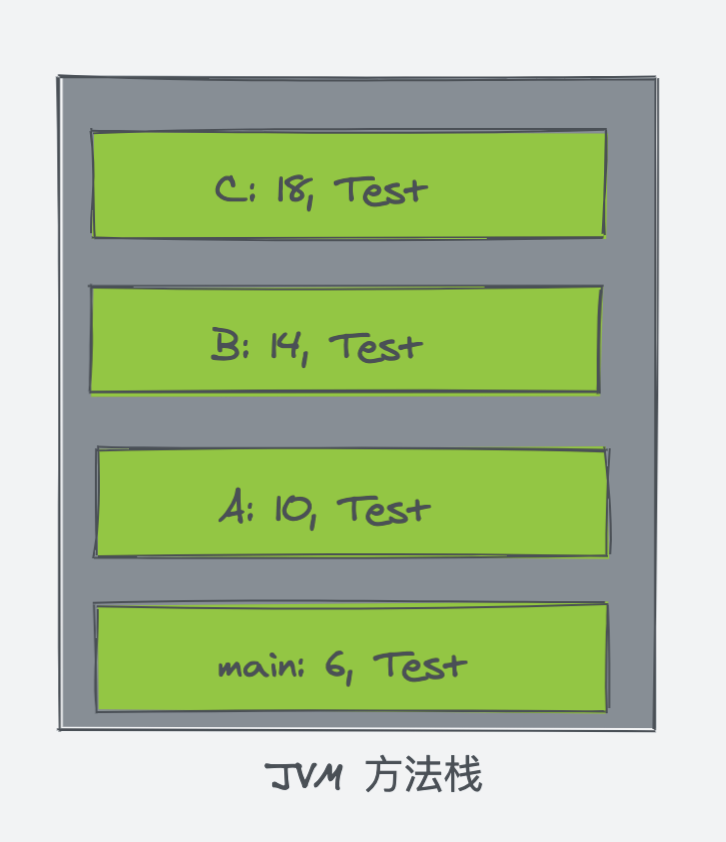
现在，JVM 方法栈的当前栈桢为 C 方法的栈桢，在 C 方法执行完毕后，C 方法的栈桢出栈。

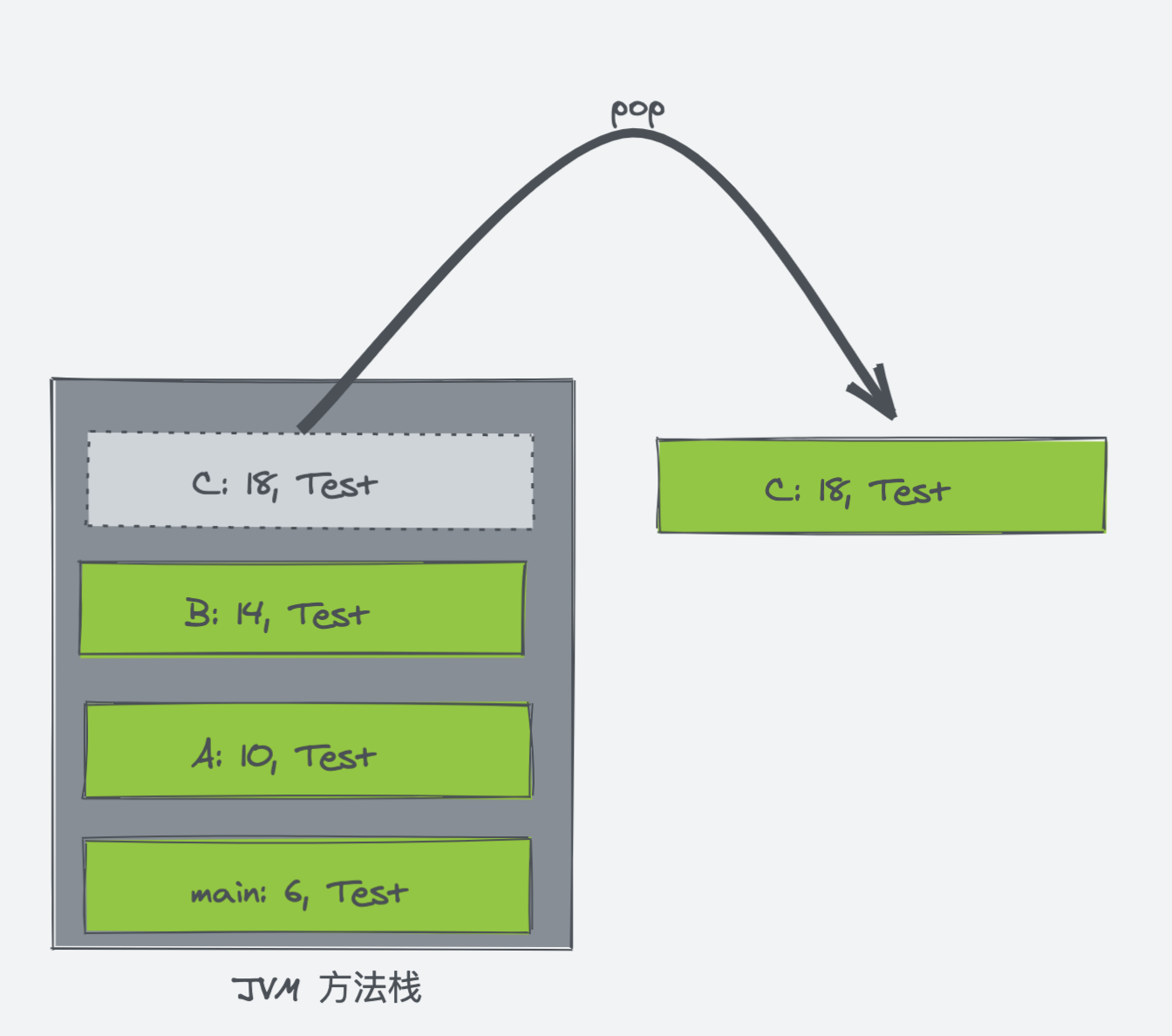
来到 B 方法的第 14 行，B 方法执行完毕后，代表 B 方法的栈桢出栈。

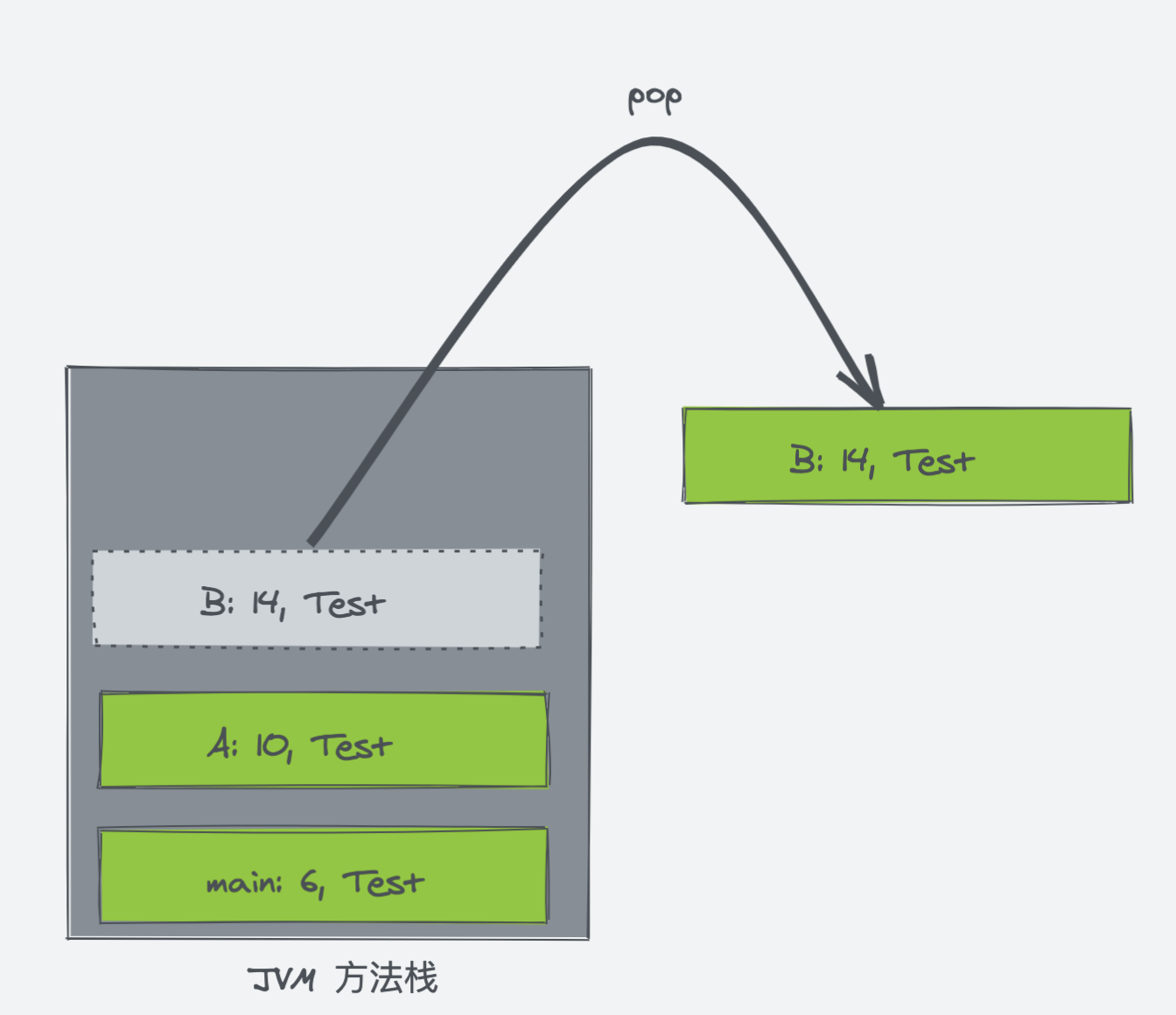
来到 A 方法的第 10 行，A 方法执行完毕后，代表 A 方法的栈桢出栈。

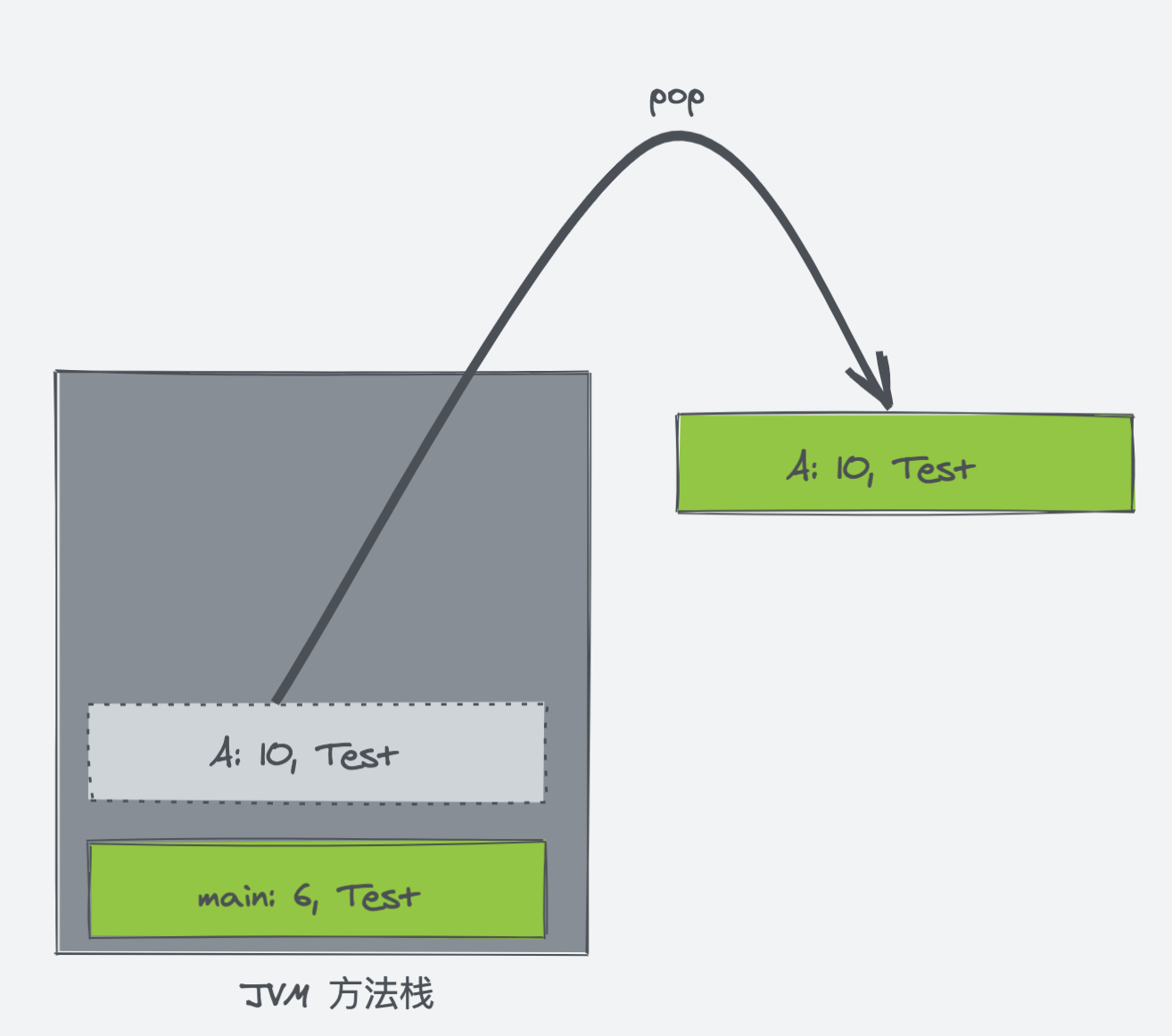
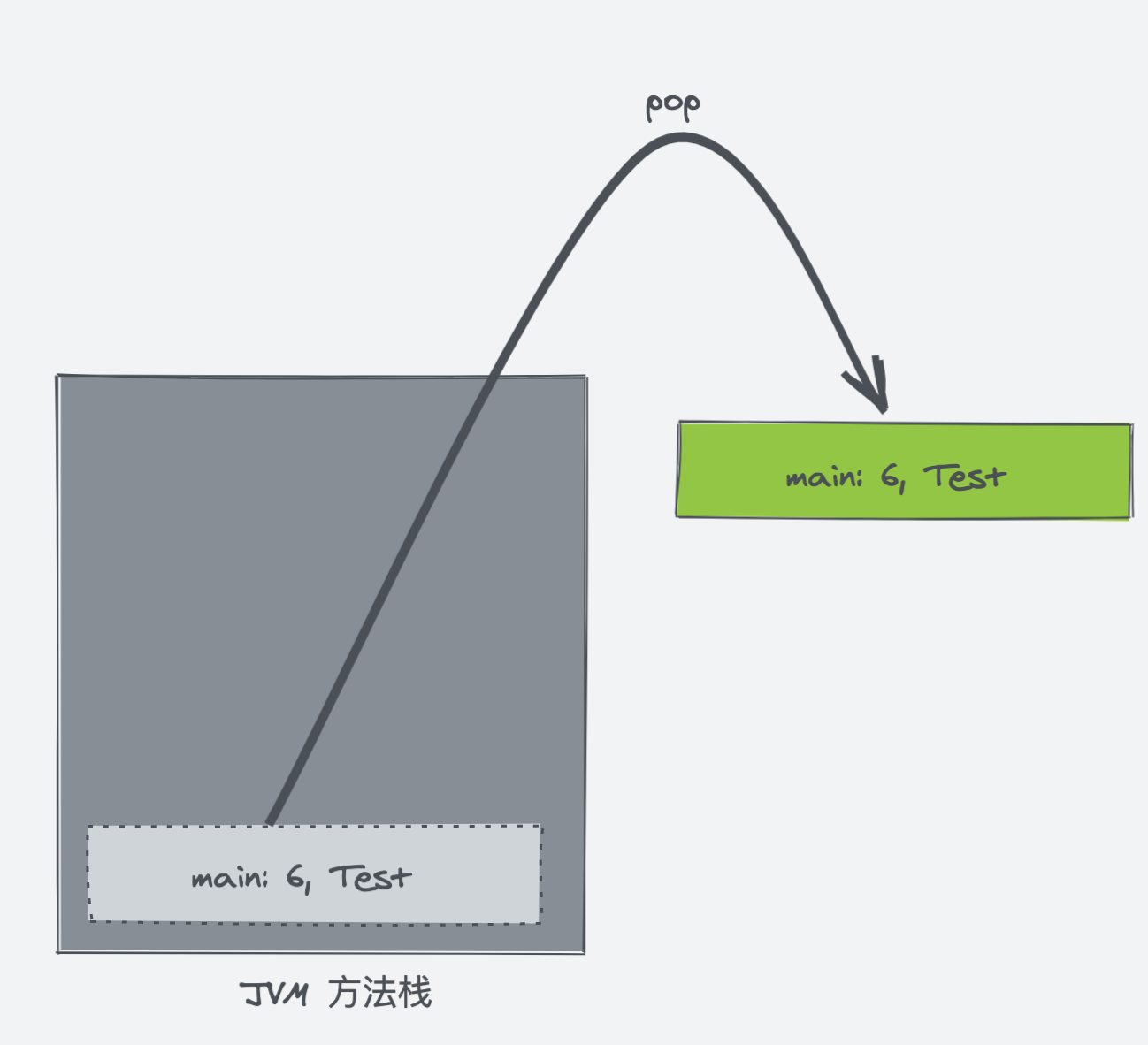
最后来到 main 方法的第 6 行，main 方法执行完毕后弹出，方法栈为空，代表所有方法已经执行完毕。

二：栈的基本实现

栈的设计上，只设计到如下几个方法：

void push(E)
E pop()
E peek()
int getSize()
boolean isEmpty()

在设计上，我们选用上一章完成的动态数组作为栈的底层实现。

代码地址

栈的复杂度分析：

push	O(1)
pop	O(1)
peek	O(1)
getSize	O(1)
isEmpty	O(1)

三：括号匹配问题

我们来看一道 LeetCode 简单题目：有效的括号

该问题涉及到了栈这种数据结构在算法当中的具体应用。

给定一个只包括 '('，')'，'{'，'}'，'['，']'的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例1:

输入：s = "{[]}"
输出：true

示例2:

输入：s = "()[]{}"
输出：true

示例3:

输入：s = "([)]"
输出：false

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/valid-parentheses

本题的解题思路：

本题使用到了栈这种数据结构，我们的算法流程如下所示

依次遍历字符串的每个字符
- 如果当前的字符为左括号，就将这个字符压栈
- 如果当前的字符为右括号：
  - 如果栈为空，则直接返回 false
  - 如果当前栈不为空，则出栈一个字符，将这个字符命名为 c_end：
    - 如果当前字符为 ')'，c_end 应为 '('，不匹配则返回 false
    - 如果当前字符为 ']'，c_end 应为 '['，不匹配则返回 false
    - 如果当前字符为 '}'，c_end 应为 '{'，不匹配则返回 false
最后返回栈是否空

代码如下：

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        char[] chars = s.toCharArray();
        for(char c : chars){
            if(c == '(' || c == '[' || c == '{'){
                stack.push(c);
            }else {
                if(!stack.isEmpty()){
                    char c_end = stack.pop();
                    if(c == ')' && c_end != '(') return false;
                    if(c == ']' && c_end != '[') return false;
                    if(c == '}' && c_end != '{') return false;
                }else {
                    return false;
                }
            }
        }
        return stack.isEmpty();
    }
}

在一些代码 IDE 中，有一类插件叫做：Rainbow Brackets（彩虹括号），用来检查括号是否闭合。它的实现原理和这道题差不多，就是应用了栈这种数据结构。

LeetCode 上有许多和栈这种数据结构相关的题目，请关注我的系列文章，在后续的【算法】章节中，我们会给出更多的示例。