算法是独立存在的一种解决问题的方法和思想。对于算法而言,实现的语言并不重要,重要的是思想。
1000000000累加求和,分别用Python和Java示例
def sum0fn(n):sum = 0for i in range(1, n + 1):sum = sum + iprint(sum)# return sumif __name__ == "__main__":res = sum0fn(1000000000)print(res)
public static void main(String[] args) {long startTime = System.currentTimeMillis();Long tar = 1000000000L;Long res = sum1(tar);System.out.println(res);/*** 获取当前的系统时间,与初始时间相减就是程序运行的毫秒数,除以1000就是秒数*/long endTime = System.currentTimeMillis();long usedTime = (endTime - startTime) / 1000;System.out.println("总耗时:" + usedTime + "秒");}// 迭代求和static Long sum1(Long num) {Long sum = 0L;for (int i = 0; i <= num; i++) {sum += i;}return sum;}
Java耗时3秒,Python3.8 耗时43秒,遇到这种问题可以通过优化算法去弥补差距。比如高斯算法求和。
算法的五大特性
- 输入: 算法具有0个或多个输入输出: 算法至少有1个或多个输出
- 有穷性: 算法在有限的步骤之后会自动结束而不会无限循环,并且每一个步骤可以在可接受的时间内完成
- 确定性:算法中的每一步都有确定的含义,不会出现二义性
- 可行性:算法的每一步都是可行的,也就是说每一步都能够执行有限的次数完成
| 执行次数函数举例 | 阶 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n2+2n+1 | O(n2) | 平方阶 |
| 5log2n+20 | O(logn) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
| 6n3+2n2+3n+4 | O(n3) | 立方阶 |
| 2n | O(2n) | 指数阶 |
注意,经常将log2n(以2为底的对数)简写成logn
常见时间复杂度对比图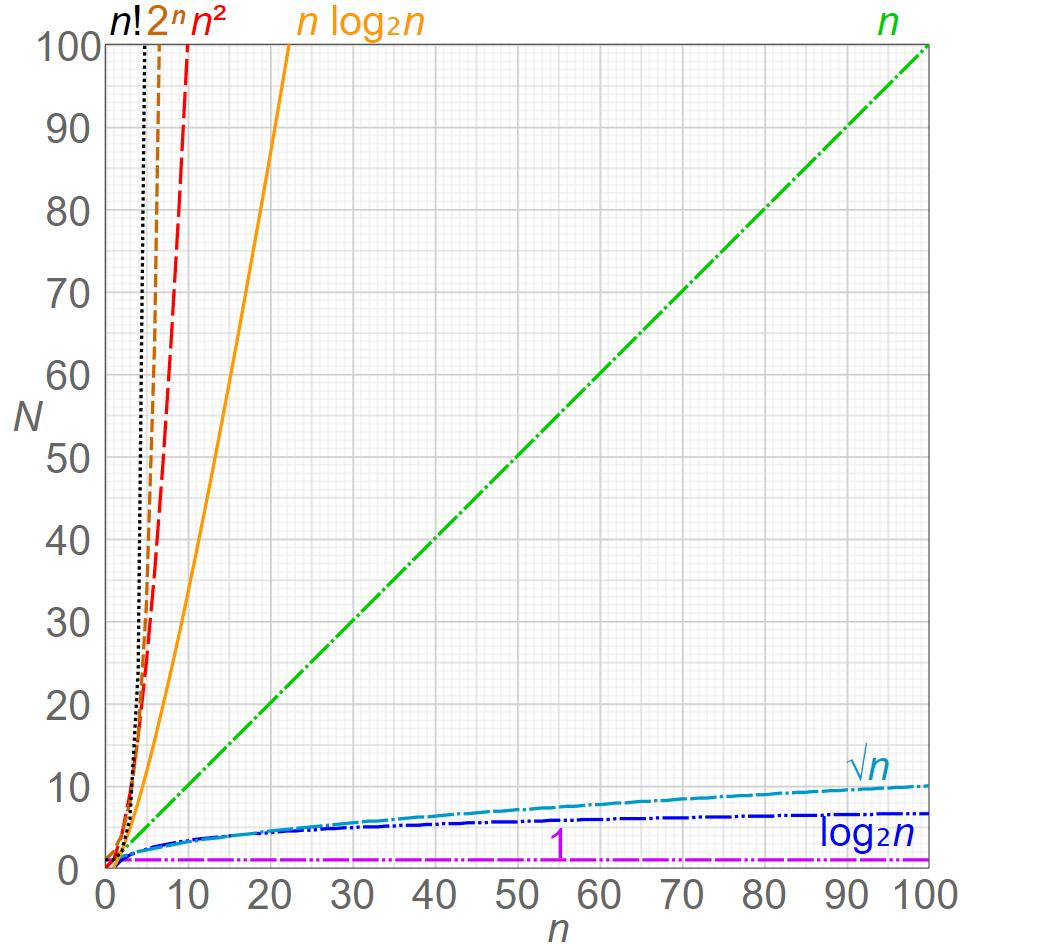
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
算法效率衡量
对于算法的时间效率,我们可以用“大O记法”来表示。
“大O记法”:对于单调的整数函数f,如果存在一个整数函数g和实常数c>0,使得对于充分大的n总有f(n)<=c*g(n),就说函数g是f的一个渐近函数(忽略常数),记为f(n)=O(g(n))。也就是说,在趋向无穷的极限意义下,函数f的增长速度受到函数g的约束,亦即函数f与函数g的特征相似。
时间复杂度:假设存在函数g,使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n)),则称O(g(n))为算法A的渐近时间复杂度,简称时间复杂度,记为T(n)。
案例:如果 a+b+c=1000,且 a^2+b^2=c^2(a,b,c 为自然数),如何求出所有a、b、c可能的组合?
时间复杂度:
T(n) = O(nnn) = O(n3)
for a in range(0, 1001):for b in range(0, 1001):for c in range(0, 1001):if a**2 + b**2 == c**2 and a+b+c == 1000:print("a, b, c: %d, %d, %d" % (a, b, c))
时间复杂度:
T(n) = O(nn(1+1)) = O(n*n) = O(n2)
for a in range(0, 1001):for b in range(0, 1001-a):c = 1000 - a - bif a**2 + b**2 == c**2:print("a, b, c: %d, %d, %d" % (a, b, c))

